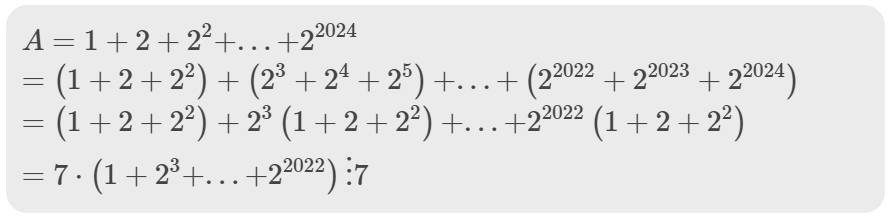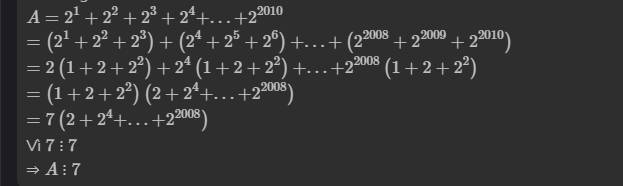A=4+2^2+2^3+....2^2023 chứng ming rằng A chia hết cho 2^2023
H24
Những câu hỏi liên quan
chứng tỏ a= 9+2 nhân 3 mũ 2+2 nhân 3 mũ 3+2nhân 3 mũ 4+ ..........+2nhân 3 mũ 2023 chia hết cho 3 mũ 2023
Lời giải:
$A=9+2.3^2+2.3^3+2.3^4+...+2.3^{2023}$
$A-9=2(3^2+3^3+3^4+...+3^{2023})$
$3(A-9)=2(3^3+3^4+3^5+...+3^{2024})$
$\Rightarrow 3(A-9)-(A-9)=2(3^{2024}-3^2)$
$2(A-9)=2.3^{2024}-18$
$\Rightarrow 2A-18=2.3^{2024}-18$
$\Rightarrow A=3^{2024}\vdots 3^{2023}$ (đpcm)
Đúng 1
Bình luận (0)
Chứng tỏ rằng A= 75( 4^2023+ 4^2022+4^2021+...+ 4^2+ 4+ 1)+ 25 chia hết cho 100
Đặt \(A=75\left(4^{2023}+4^{2022}+...+4^2+4+1\right)+25\)
Đặt \(B=4^{2023}+4^{2022}+...+4^2+4+1\)
=>\(4B=4^{2024}+4^{2023}+...+4^3+4^2+4\)
=>\(4B-B=4^{2024}+4^{2023}+...+4^3+4^2+4-4^{2023}-4^{2022}-...-4^2-4-1\)
=>\(3B=4^{2024}-1\)
=>\(B=\dfrac{4^{2024}-1}{3}\)
\(A=75\left(4^{2023}+4^{2022}+...+4^2+4+1\right)+25\)
\(=75\cdot\dfrac{4^{2024}-1}{3}+25\)
\(=25\cdot\left(4^{2024}-1\right)+25\)
\(=25\cdot4^{2024}\)
\(=25\cdot4\cdot4^{2023}=100\cdot4^{2023}⋮100\)
Đúng 0
Bình luận (0)
A= 75.( 4^2023 + 4^2022 +...+ 4^2 + 5) + 25. Chứng minh rằng A chia hết cho 4^2024. Giúp mình với ạ, cảm ơn nhiều.
chứng minh rằng: 5^2022+2^2023 chia hết cho 3
Tham khảo
\(\text{+)}\)Ta có:\(5\equiv-1\left(mod3\right)\)
\(\Rightarrow5^{2022}\equiv\left(-1\right)^{2022}\left(mod3\right)\left(1\right)\)
\(\text{+)}\)Ta có:\(2\equiv-1\left(mod3\right)\)
\(\Rightarrow2^{2023}\equiv\left(-1\right)^{2023}\left(mod3\right)\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\Rightarrow5^{2022}+5^{2023}\equiv0\left(mod3\right)\)
Vậy...
Đúng 0
Bình luận (0)
cho A= 3/2^2+8/3^3+15/4^2+......+2023^2-1/2023^2 chứng minh rằng biểu thức a có giá trị là một số tự nhiên
cho a=2020+2020^2+2022^3+...+2020^2 chứng minh rằng Achia hết cho 2023
Biểu thức A viết có vẻ không đúng. Bạn xem lại đề.
Đúng 0
Bình luận (0)
Chứng minh rằng:
a) A = 5 + 5^2 + 5^3 + …+ 5^100 chia hết cho 5 nhưng không chia hết chi 25
b) B = 5 + 5^2 + 5^3 + …+ 5^20 chia hết cho 6
c) C = 5 + 5^2 + 5^3 + …+ 5^2022 + 5^2023 không chia hết cho 6
d) D = 1 + 2 + 2^2 + 2^3 + …+ 2^2021 chia hết cho 7
a) Ta có:
\( A = 5+5^2+5^3+\ldots+5^{100} \)
Để chứng minh A chia hết cho 5, ta xét tổng S = \( 5+5^2+5^3+\ldots+5^{100} \) (mod 5).
Ta thấy rằng \( 5 \) chia hết cho 5, \( 5^2 \) chia hết cho 5, \( 5^3 \) chia hết cho 5, và tiếp tục như vậy cho tới \( 5^{100} \).
Vì vậy, ta có: \( S \equiv 0+0+0+\ldots+0 \equiv 0 \) (mod 5).
Do đó, A chia hết cho 5.
Để chứng minh A không chia hết cho 25, ta xét tổng T = \( 5+5^2+5^3+\ldots+5^{100} \) (mod 25).
Ta thấy rằng \( 5 \) không chia hết cho 25, \( 5^2 \) không chia hết cho 25, \( 5^3 \) không chia hết cho 25, và tiếp tục như vậy cho tới \( 5^{100} \).
Vì vậy, ta có: \( T \equiv 5+0+0+\ldots+0 \equiv 5 \) (mod 25).
Do đó, A không chia hết cho 25.
b) Ta có:
\( B = 5+5^2+5^3+\ldots+5^{20} \)
Để chứng minh B chia hết cho 6, ta xét tổng U = \( 5+5^2+5^3+\ldots+5^{20} \) (mod 6).
Ta thấy rằng \( 5 \) chia hết cho 6, \( 5^2 \) không chia hết cho 6, \( 5^3 \) không chia hết cho 6, \( 5^4 \) chia hết cho 6, và tiếp tục như vậy cho tới \( 5^{20} \).
Vì vậy, ta có: \( U \equiv 5+1+1+\ldots+1 \equiv 5 \) (mod 6).
Do đó, B chia hết cho 6.
c) Ta có:
\( C = 5+5^2+5^3+\ldots+5^{2022}+5^{2023} \)
Để chứng minh C không chia hết cho 6, ta xét tổng V = \( 5+5^2+5^3+\ldots+5^{2022}+5^{2023} \) (mod 6).
Ta thấy rằng \( 5 \) chia hết cho 6, \( 5^2 \) không chia hết cho 6, \( 5^3 \) không chia hết cho 6, \( 5^4 \) chia hết cho 6, và tiếp tục như vậy cho tới \( 5^{2022} \) và \( 5^{2023} \).
Vì vậy, ta có: \( V \equiv 5+1+1+\ldots+1 \equiv 2 \) (mod 6).
Do đó, C không chia hết cho 6.
d) Ta có:
\( D = 1+2+2^2+2^3+\ldots+2^{2021} \)
Để chứng minh D chia hết cho 7, ta xét tổng W = \( 1+2+2^2+2^3+\ldots+2^{2021} \) (mod 7).
Ta thấy rằng \( 2 \) không chia hết cho 7, \( 2^2 \) chia hết cho 7, \( 2^3 \) không chia hết cho 7, \( 2^4 \) không chia hết cho 7, \( 2^5 \) không chia hết cho 7, \( 2^6 \) chia hết cho 7, và tiếp tục
mong mn cho minh vai xu :)))))))))))))))))))))))))))))))))
Đúng 2
Bình luận (0)
a, A = 5 + 52 + 53 + ... + 5100
A = 5. ( 1 + 5 + ...+ 599)
5 ⋮ 5 ⇒A = 5.(1 + 5 + ...+ 599) ⋮ 5 (1)
A = 5 + 52 + 53 + ... + 5100
A = 5 + 52.( 1 + 5 + 52 + ... + 598)
A = 5 + 25 . ( 1 + 5 + 52 +...+ 598)
Vì 25 ⋮ 25 nên 25.(1 + 5 + 52 +... + 598) ⋮ 25
5 không chia hết cho 25 nên
A = 5 + 25.( 1 + 5 +...+ 598) không chia hết cho 25 (2)
Kết hợp (1) và (2) ta có:
A ⋮ 5 nhưng không chia hết cho 25 (đpcm)
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
CMR: A\(=2\left(1^{2023}+2^{2023}+...+2022^{2023}\right)\) chia hết cho 2022
Lời giải:
\(A=2.2022^{2023}+2(1^{2023}+2^{2023}+3^{2023}+...+1010^{2023}+1011^{2023}+1012^{2023}+...+2021^{2023})\)
\(=2.2022^{2023}+2[(1^{2023}+2021^{2023})+(2^{2023}+2019^{2023})+...+(1010^{2023}+1012^{2023})+1011^{2023}]\)
\(=2.2022^{2023}+2.1011^{2023}+2[(1^{2023}+2021^{2023})+(2^{2023}+2019^{2023})+...+(1010^{2023}+1012^{2023})]\)
Dễ thấy: $2.2022^{2023}\vdots 2022; 2.1011^{2023}=2022.1011^{2023}\vdots 2022$
Đối với biểu thức trong ngoặc vuông thì: Nhớ rằng với mọi $n$ lẻ thì $a^n+b^n\vdots a+b$ nên $1^{2023}+2021^{2023}\vdots 2022; 2^{2023}+2019^{2023}\vdots 2022;...; 1010^{2023}+1012^{2023}\vdots 2022$
$\Rightarrow 2[(1^{2023}+2021^{2023})+(2^{2023}+2019^{2023})+....+(1010^{2023}+1012^{2023})]\vdots 2022$
Do đó $A\vdots 2022$
Đúng 4
Bình luận (0)
cho A = 1+2+2^2+....+2^2023+262024. chứng tỏ A chia hết cho 7