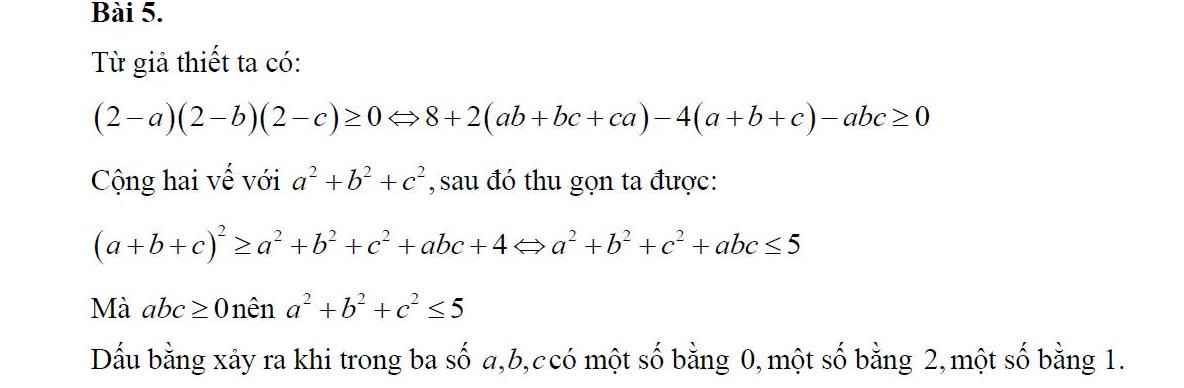(a^2+b^2+c^2) x 2 = 2 x (a^4+b^4+c^4)

suy ra: (a+b+c)^2 x 2 = (a+b+c)^4 x 2

Mà a+b+c= 0(gt)

suy ra: 0^2 x 2=0^4 x 2

0 = 0

=)))

1) ta có: A= x^3 -8y^3=> A=(x-2y)(x^2 +2xy+4y^2)=>A=5.(29+2xy)   (vì x-2y=5 và x^2+4y^2=29)     (1)

Mặt khác : x-2y=5(gt)=> (x-2y)^2=25=> x^2-4xy+4y^2=25=>29-4xy=25(vì x^2+4y^2=29)

                                                                                          => xy=1    (2)

Thay (2) vào (1) ta đc: A= 5.(29+2.1)=155

Vậy gt của bt A là 155

2) theo bài ra ta có: a+b+c=0 => a+b=-c=>(a+b)^2=c^2=> a^2 +b^2+2ab=c^2=>c^2-a^2-b^2=2ab

=> \(\left(c^2-a^2-b^2\right)^2=4a^2b^2\)

=>\(c^4+a^4+b^4-2c^2a^2+2a^2b^2-2b^2c^2=4a^2b^2\)

=>\(a^4+b^4+c^4=2a^2b^2+2b^2c^2+2c^2a^2\)

=>\(2\left(a^4+b^4+c^4\right)=\left(a^2+b^2+c^2\right)^2\)

=> \(a^4+b^4+c^4=\frac{1}{2}\left(a^2+b^2+c^2\right)^2\) (đpcm)

BĐT này do giáo sư Vasile đề xuất, và đây là lời giải của ông ấy:

Do vai trò của các biến là như nhau, ko mất tính tổng quát, giả sử \(a^2=max\left\{a^2;b^2;c^2;d^2\right\}\)

\(\Rightarrow a^2\ge\dfrac{b^2+c^2+d^2}{3}\)

Đặt \(x^2=\dfrac{b^2+c^2+d^2}{3}\Rightarrow x^2\le a^2\) (1)

Đồng thời \(x^2=\dfrac{b^2+c^2+d^2}{3}\ge\dfrac{1}{9}\left(b+c+d\right)^2=\dfrac{a^2}{9}\Rightarrow a^2\le9x^2\) (2)

\(\left(1\right);\left(2\right)\Rightarrow\left(a^2-x^2\right)\left(a^2-9x^2\right)\le0\) (3)

Ta có:

\(b^4+c^4+d^4=\left(b^2+c^2+d^2\right)^2-2\left(b^2c^2+c^2d^2+b^2d^2\right)\le\left(b^2+c^2+d^2\right)^2-\dfrac{2}{3}\left(bc+cd+bd\right)^2\)

\(=\left(b^2+c^2+d^2\right)^2-\dfrac{1}{6}\left[\left(b+c+d\right)^2-\left(b^2+c^2+d^2\right)\right]^2=9x^4-\dfrac{1}{6}\left(a^2-3x^2\right)^2=\dfrac{45x^4+6a^2x^2-a^4}{6}\)

Do đó:

\(12\left(a^4+b^4+c^4+d^4\right)\le12a^4+12.\dfrac{45x^4+6a^2x^2-a^4}{6}=90x^4+12a^2x^2+10a^4\)

Nên ta chỉ cần chứng minh:

\(7\left(a^2+3x^2\right)^2\ge90x^4+12a^2x^2+10a^4\)

\(\Leftrightarrow a^4-10a^2x^2+9x^4\le0\)

\(\Leftrightarrow\left(a^2-9x^2\right)\left(a^2-x^2\right)\le0\) (đúng theo (3))

Vậy BĐT được chứng minh hoàn tất.

Dấu "=" xảy ra khi \(b=c=d=-\dfrac{a}{3}\) và các hoán vị của chúng

Bài 3:

\(\dfrac{1}{\left(x-y\right)^2}+\dfrac{1}{x^2}+\dfrac{1}{y^2}\ge\dfrac{4}{xy}\)

\(\Leftrightarrow x^2y^2\left(\dfrac{1}{\left(x-y\right)^2}+\dfrac{1}{x^2}+\dfrac{1}{y^2}\right)\ge\dfrac{4}{xy}.x^2y^2\)

\(\Leftrightarrow\dfrac{x^2y^2}{\left(x-y\right)^2}+x^2+y^2\ge4xy\)

\(\Leftrightarrow\dfrac{x^2y^2}{\left(x-y\right)^2}+x^2-2xy+y^2\ge2xy\)

\(\Leftrightarrow\left(\dfrac{xy}{x-y}\right)^2+\left(x-y\right)^2\ge2xy\)

\(\Leftrightarrow\left(\dfrac{xy}{x-y}\right)^2-2xy+\left(x-y\right)^2\ge0\)

\(\Leftrightarrow\left(\dfrac{xy}{x-y}-x+y\right)^2=0\) (luôn đúng)

-Tham khảo:

-Tham khảo: