Nhờ các bạn và thầy cô hưỡng dẫn ạ...
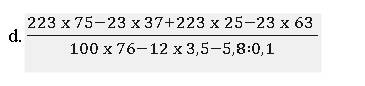
Nhờ thầy cô và các bạn hướng dẫn dùm em ạ
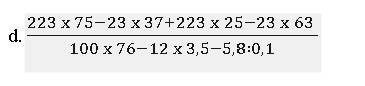
\(\dfrac{223\times75-23\times37+223\times25-23\times63}{100\times76-12\times3,5-5,8:0,1}\\ =\dfrac{223\times\left(75+25\right)-23\times\left(37+63\right)}{100\times76-42-58}\\ =\dfrac{\left(223-23\right)\times100}{100\times76-100}\\ =\dfrac{200\times100}{100\times75}=\dfrac{200}{75}=\dfrac{200:25}{75:25}=\dfrac{8}{3}\)
Nhờ thầy cô và các bạn giúp đỡ với ạ
Lời giải:
Gọi số công nhân mỗi đội lần lượt là $a,b,c$. Vì số công nhân tỉ lệ nghịch với số
ngày làm nên $4a=6b=8c=\frac{a}{\frac{1}{4}}=\frac{b}{\frac{1}{6}}=\frac{c}{\frac{1}{8}}$
Áp dụng TCDTSBN:
$\frac{a}{\frac{1}{4}}=\frac{b}{\frac{1}{6}}=\frac{c}{\frac{1}{8}}=\frac{a-b}{\frac{1}{4}-\frac{1}{6}}=\frac{4}{\frac{1}{12}}=48$
$\Rightarrow a=48.\frac{1}{4}=12; b=48.\frac{1}{6}=8; c=48.\frac{1}{8}=6$
Nhờ thầy cô và các bạn giúp đỡ em với ạ
Nhờ thầy cô và các bạn giúp đỡ với ạ. Em cám ơn nhiều ạ!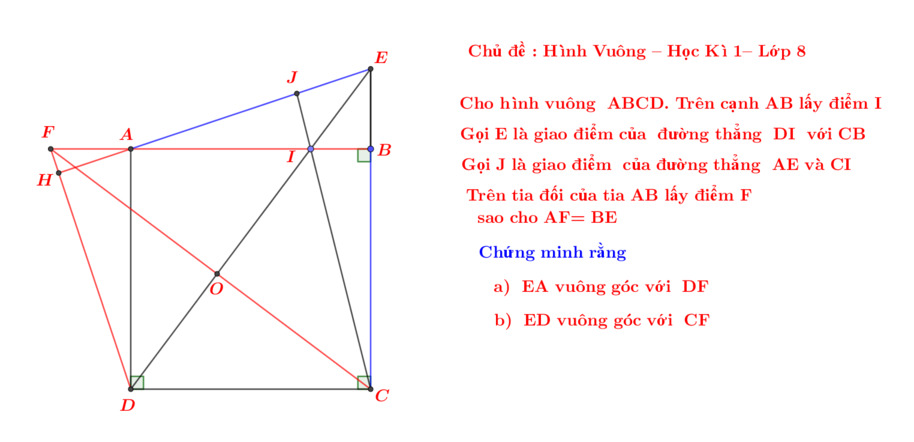
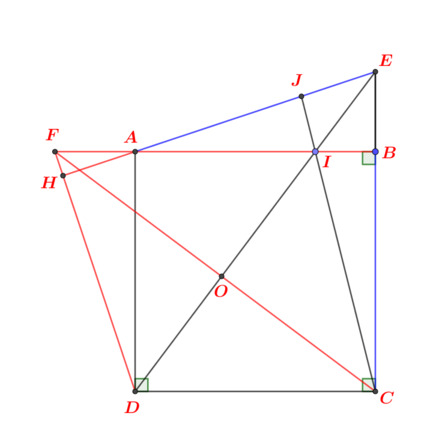
Nhờ thầy cô và các bạn giúp em ạ. Em cảm ơn.
14.
\(\left(ab+c\right)\left(bc+a\right)\le\dfrac{1}{4}\left(ab+bc+c+a\right)^2=\dfrac{1}{4}\left(a+c\right)^2\left(b+1\right)^2\)
Tương tự:
\(\left(ab+c\right)\left(ca+b\right)\le\dfrac{1}{4}\left(b+c\right)^2\left(a+1\right)^2\)
\(\left(bc+a\right)\left(ca+b\right)\le\dfrac{1}{4}\left(a+b\right)^2\left(c+1\right)^2\)
Nhân vế với vế và khai căn:
\(\left(ab+c\right)\left(bc+a\right)\left(ca+b\right)\le\dfrac{1}{8}\left(a+b\right)\left(b+c\right)\left(c+a\right)\left(a+1\right)\left(b+1\right)\left(c+1\right)\)
Mặt khác ta có:
\(\left(a+1\right)\left(b+1\right)\left(c+1\right)\le\dfrac{1}{27}\left(a+b+c+3\right)^3=8\)
\(\Rightarrow\left(ab+c\right)\left(bc+a\right)\left(ca+b\right)\le\dfrac{1}{8}.8.\left(a+b\right)\left(b+c\right)\left(c+a\right)\)
Dấu "=" xảy ra khi...
15.
\(\Leftrightarrow\sum\dfrac{2a^2}{2a^2+\left(b+c-a\right)^2}\le2\)
\(\Leftrightarrow\sum\left(\dfrac{2a^2}{2a^2+\left(b+c-a\right)^2}-1\right)\le2-3\)
\(\Leftrightarrow\sum\dfrac{\left(b+c-a\right)^2}{2a^2+\left(b+c-a\right)^2}\ge1\)
Đặt \(\left\{{}\begin{matrix}b+c-a=x\\c+a-b=y\\a+b-c=z\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=\dfrac{y+z}{2}\\b=\dfrac{x+z}{2}\\c=\dfrac{x+y}{2}\end{matrix}\right.\)
\(VT=\sum\dfrac{x^2}{2\left(\dfrac{y+z}{2}\right)^2+x^2}=\sum\dfrac{2x^2}{2x^2+\left(y+z\right)^2}\ge\sum\dfrac{2x^2}{2x^2+2\left(y^2+z^2\right)}=1\)
Dấu "=" xảy ra khi...
Nhờ Thầy/Cô và các bạn phương pháp giải bài này ạ? Kết Quả và Phương Pháp ạ?
Em ơi, em cần phương pháp giải dạng nào. và bài tập cụ thể là như nào vậy em, phải có đề bài cụ thể thì thầy cô mới hướng dẫn được em nhé
Nhờ thầy cô giáo và các bạn giúp đỡ theo kiến thức học kì 1 -- Toán Lớp 8 với ạ.
Cám ơn thầy cô nhiều ạ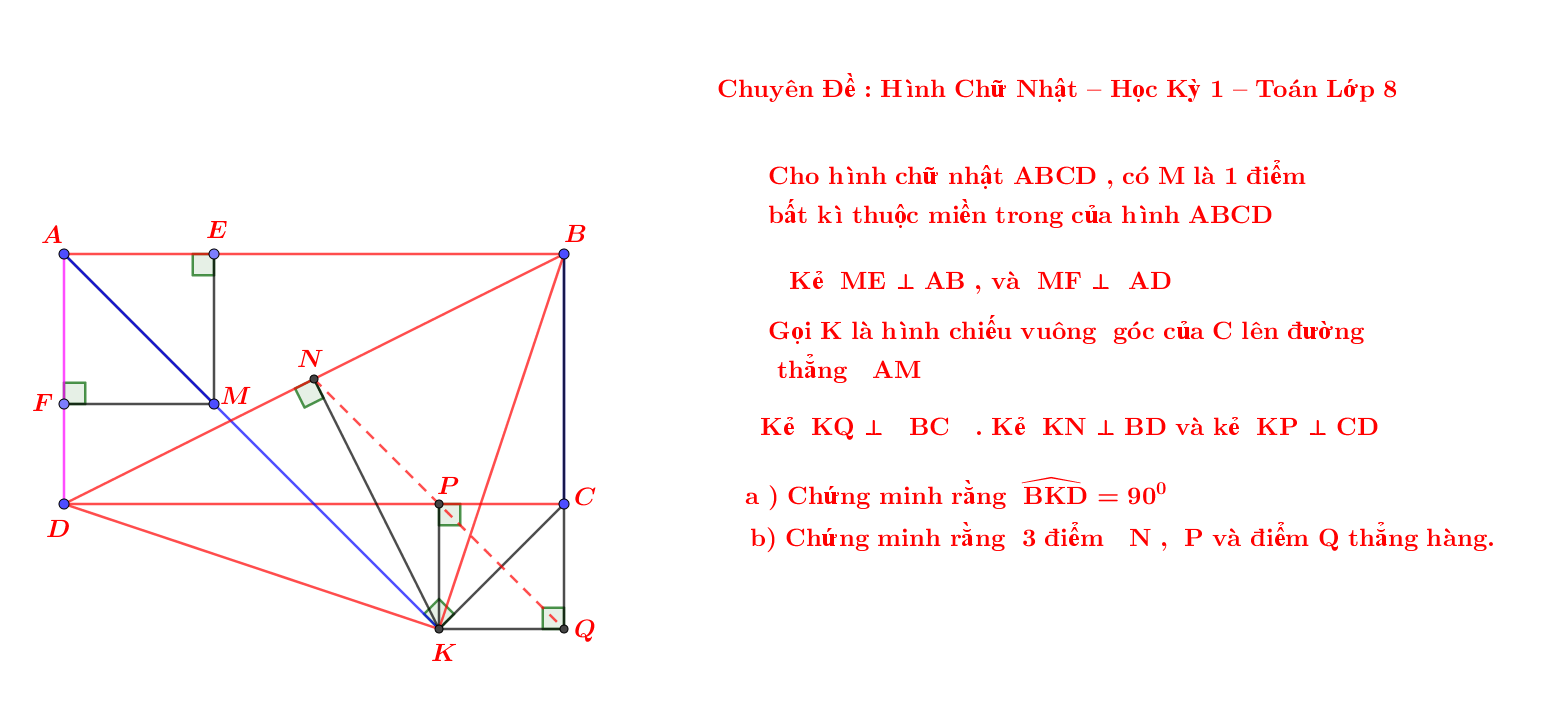
Nhờ thầy cô và các bạn trong nhóm giúp đỡ em với ạ!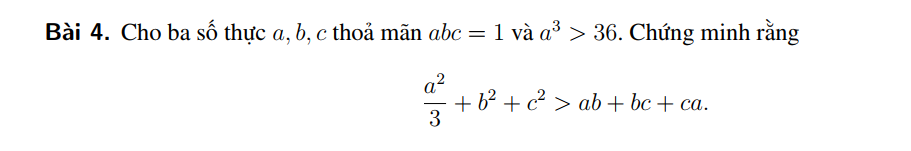
Từ GT \(\Leftrightarrow a>0;bc>0\)
\(BĐT\Leftrightarrow\dfrac{a^2}{3}+\left(b+c\right)^2-3bc-a\left(b+c\right)\ge0\\ \Leftrightarrow\dfrac{1}{3}+\left(\dfrac{b+c}{a}\right)^2-\dfrac{b+c}{a}-\dfrac{3}{a^2}\ge0\)
Vì \(a^3>36\) nên
\(\dfrac{1}{3}+\left(\dfrac{b+c}{a}\right)^2-\dfrac{b+c}{a}-\dfrac{3}{a^2}\\ >\left(\dfrac{b+c}{a}\right)^2-\dfrac{b+c}{a}+\dfrac{1}{4}=\left(\dfrac{b+c}{a}-\dfrac{1}{2}\right)^2\ge0\)
Nhờ thầy cô và các bạn giúp em câu 1.1.16 và 1.1.17 ạ. Em cảm ơn.