bài 8:hình14 : giúp với
TR
Những câu hỏi liên quan
giúp em bài 8 bài 9 với ạ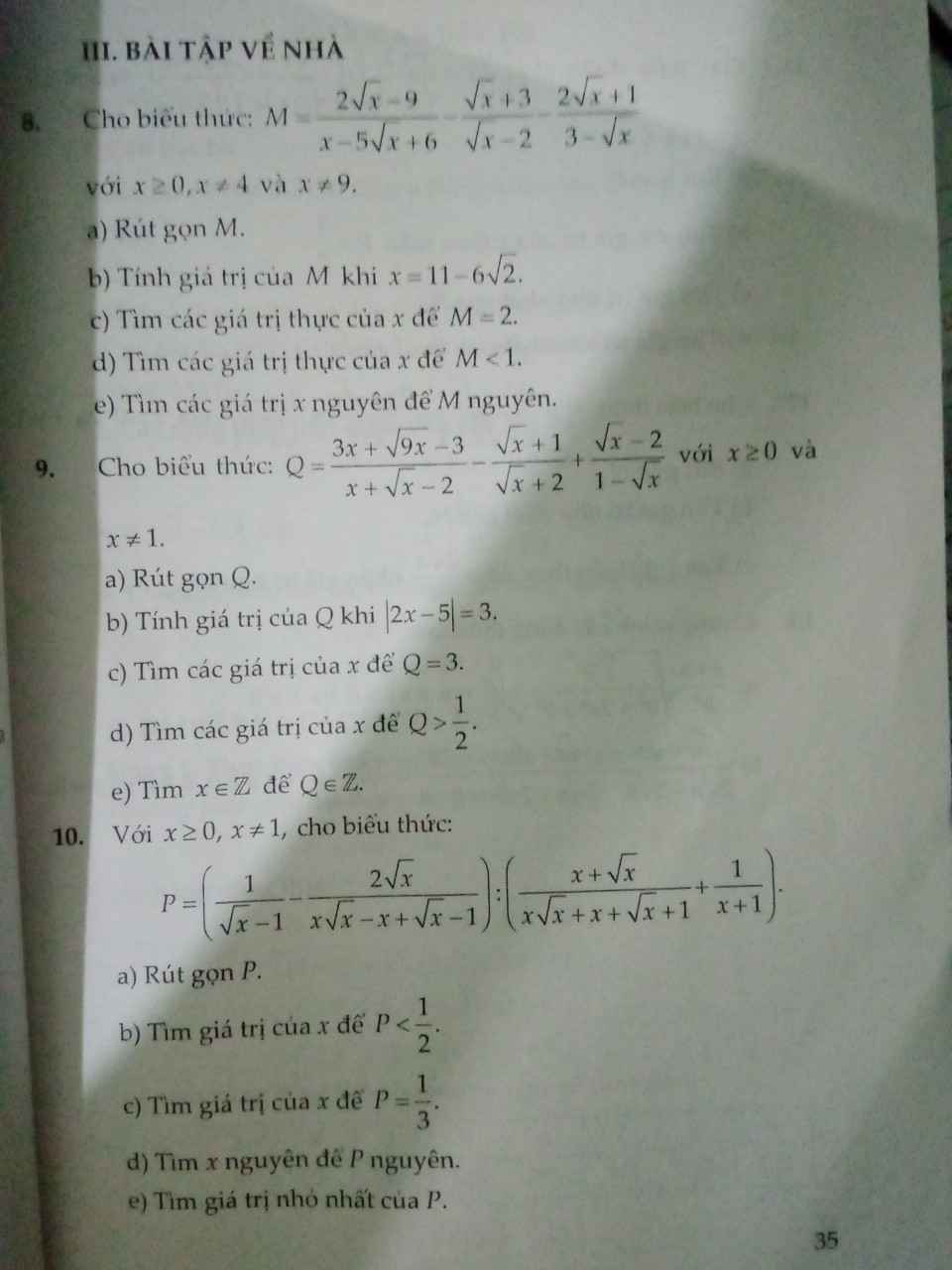
Bài 8:
a: Ta có: \(M=\dfrac{2\sqrt{x}-9}{x-5\sqrt{x}+6}-\dfrac{\sqrt{x}+3}{\sqrt{x}-2}+\dfrac{2\sqrt{x}+1}{\sqrt{x}-3}\)
\(=\dfrac{2\sqrt{x}-9-x+9+2x-4\sqrt{x}+\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)
b: Thay \(x=11-6\sqrt{2}\) vào M, ta được:
\(M=\dfrac{3-\sqrt{2}+1}{3-\sqrt{2}-3}=\dfrac{4-\sqrt{2}}{-\sqrt{2}}=-2\sqrt{2}+1\)
Đúng 0
Bình luận (0)
Bài 8:
a) \(M=\dfrac{2\sqrt{x}-9-\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)+\left(2\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{2\sqrt{x}-9-x+9+2x-3\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{x-\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)
b) \(M=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}=\dfrac{\sqrt{11-6\sqrt{2}}+1}{\sqrt{11-6\sqrt{2}}-3}=\dfrac{\sqrt{\left(3-\sqrt{2}\right)^2}+1}{\sqrt{\left(3-\sqrt{2}\right)^2}-3}=\dfrac{4-\sqrt{2}}{-\sqrt{2}}=1-2\sqrt{2}\)
c) \(M=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}=3\)
\(\Leftrightarrow3\sqrt{x}-9=\sqrt{x}+1\Leftrightarrow2\sqrt{x}=10\Leftrightarrow\sqrt{x}=5\Leftrightarrow x=25\left(tm\right)\)
d) \(M=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}< 1\)
\(\Leftrightarrow\sqrt{x}+1< \sqrt{x}-3\Leftrightarrow1< -3\left(VLý\right)\)
Vậy \(S=\varnothing\)
e) \(M=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}=1+\dfrac{4}{\sqrt{x}-3}\in Z\)
\(\Rightarrow\sqrt{x}-3\inƯ\left(4\right)=\left\{-4;-2;-1;1;2;4\right\}\)
Kết hợp đk:
\(\Rightarrow x\in\left\{1;16;25;49\right\}\)
Đúng 1
Bình luận (0)
Làm giúp em bài 6 đến bài 8 với ạ

Giải giúp từ bài 2 đến bài 8 với ạ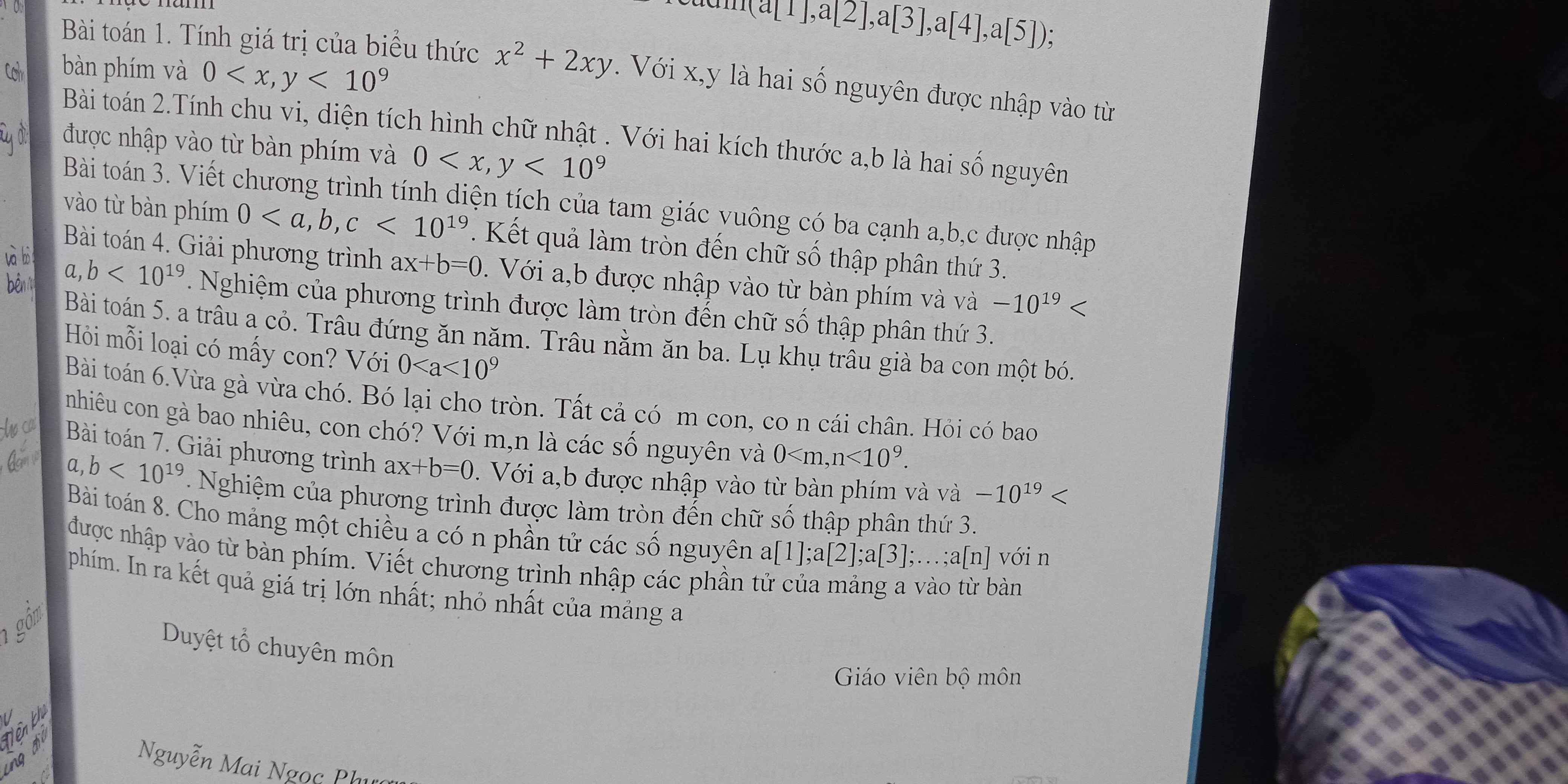
Bài 2:
#include <bits/stdc++.h>
using namespace std;
long long a,b;
int main()
{
cin>>a>>b;
cout<<(a+b)*2<<endl;
cout<<a*b;
return 0;
}
Đúng 0
Bình luận (0)
 giúp mình bài 7, bài 8 với ạ, cảm ơn nhiều
giúp mình bài 7, bài 8 với ạ, cảm ơn nhiều
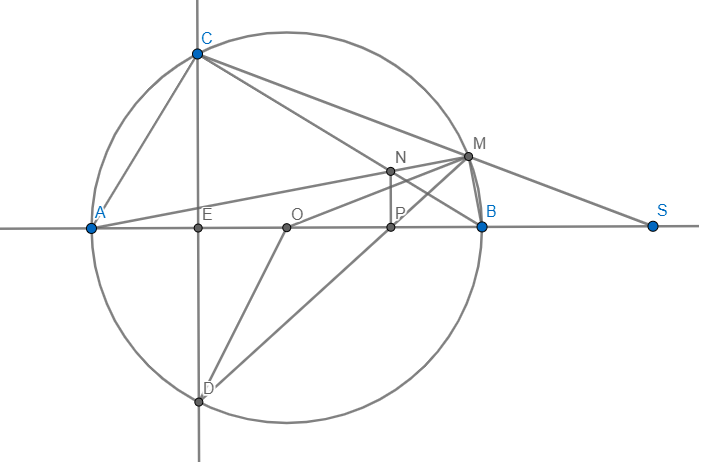
giúp mình bài 8 với
a) ACMB nội tiếp \(\Rightarrow\angle MCB=\angle MAB\)
Xét \(\Delta SMA\) và \(\Delta SBC:\) Ta có: \(\left\{{}\begin{matrix}\angle SCB=\angle SAM\\\angle ASCchung\end{matrix}\right.\)
\(\Rightarrow\Delta SMA\sim\Delta SBC\left(g-g\right)\)
b) CD cắt AB tại E
Vì AB là đường kính \(\Rightarrow\angle ACB=\angle AMB=90\)
ACMD nội tiếp \(\Rightarrow\angle AMD=\angle ACD=\angle ACE=\angle ABC\left(=90-\angle CAB\right)\)
\(\Rightarrow\angle NMP=\angle NBP\Rightarrow NMBP\) nội tiếp
mà \(\angle NMB=90\Rightarrow\angle NPB=90\Rightarrow NP\bot AB\)
mà \(CD\bot AB\Rightarrow\) \(NP\parallel CD\)
c) Vì \(\Delta OMD\) cân tại O \(\Rightarrow\angle OMP=\dfrac{180-\angle DOM}{2}=90-\dfrac{1}{2}\angle DOM\)
\(=90-\angle DCM=90-\angle ECS=\angle OSM\)
Xét \(\Delta OMP\) và \(\Delta OSM:\) Ta có: \(\left\{{}\begin{matrix}\angle OMP=\angle OSM\\\angle MOSchung\end{matrix}\right.\)
\(\Rightarrow\Delta OMP\sim\Delta OSM\left(g-g\right)\Rightarrow\dfrac{OM}{OS}=\dfrac{OP}{OM}\Rightarrow OM^2=OP.OS\)
Đúng 2
Bình luận (0)
giúp mk bài 8 với
a: \(\left\{{}\begin{matrix}2x+y=4\\x-2y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x+2y=8\\x-2y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=0\end{matrix}\right.\)
Đúng 1
Bình luận (1)
Giúp mình bài 8 với

Bài 8:
Theo đề: \(y=kx;y=\dfrac{k}{a}\cdot z\Leftrightarrow kx=\dfrac{k}{a}\cdot z\Leftrightarrow x=\dfrac{k}{a}\cdot z\cdot\dfrac{1}{k}=\dfrac{1}{a}\cdot z\)
Vậy x tlt z với hệ số tỉ lệ \(\dfrac{1}{a}\)
Đúng 0
Bình luận (0)
Ai giúp mình bài này với ạ =v
3^8+4^8+5^8+...+800^8
38 + 48 + 58 + ... + 8008 (cùng số mũ)
⇒ (3.4.5.6.7......800)8
Phép này chỉ làm được đến đây thôi, chứ nhân thì ra số dài lắm bạn.
Đúng 0
Bình luận (0)
giúp e bài 5 đến bài 8 với ạ,e cảm ơn
Bài 7:
a: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HE là đường cao ứng với cạnh huyền AB, ta được:
\(AE\cdot AB=AH^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔHAC vuông tại H có HF là đường cao ứng với cạnh huyền AC, ta được:
\(AF\cdot AC=AH^2\left(2\right)\)
Từ (1), (2) suy ra \(AE\cdot AB=AF\cdot AC\)
Đúng 1
Bình luận (0)






