Cho hình thang ABCD ( AD song song BC ).Gọi AC là tia phân giác của góc A. CM : AB = BC
PH
Những câu hỏi liên quan
Cho hình thang cân ABCD, (góc CA=60 độ, BC song song AD), AC là tia phân giác của góc A, BC=5cm
a,Chứng minh tam giác ABC là tam giác cân
b, Chứng minh tam giác ABC là tam giác vuông
c,Tính chu vi hình thang ABCD
1.cho hình thang ABCD biết góc A=góc B=90 độ AB=BC=1/2AD
a, tính các góc của hình thang
b,cm AC vuông góc với CD
c, tính chu vi của hình thang biết AB=3cm
2.cho hình thang ABCD (AB SONG SONG CD)trong đó đáy CD=BC+AD
CMR 2 tia phân giác của góc A VÀ GÓC B cắt nhau tại 1 điểm thuộc cạnh đáy CD
GIÚP MK NHA THANKS CÁC BN NHÌU MOAH
Bài 2:
Gọi AI là phân giác của góc BAD
Xét ΔDAI có góc DAI=góc DIA
nên ΔDIA cân tại D
=>DA=DI
=>CB=CI
=>ΔCBI cân tại C
=>góc CBI=góc CIB
=>góc CBI=góc ABI
=>BI là phân giác của góc ABC(ĐPCM)
Đúng 0
Bình luận (0)
Cho hình thang ABCD( AD//BC) có AC là tia phân giác của góc A
CM: AB=BC.
Vì AD//BC
=> góc DAC = góc BCA. ( so le trong)
Mà góc DAC = góc BAC ( AC là p/giác góc A)
=>góc BAC= goc BCA
=> tam giác BAC cân tại B
=>AB=BC
Vậy _____________
Đúng 0
Bình luận (0)
Bài 1 : Cho hình thang cân ABCD (AD // BC) có góc A 60 độ , AD 4 cm và BC 2 cm. Qua B kẻ đường thẳng song song với CD cắt AD ở E.1) Tính ED.2) Chứng minh tam giác ABE đều.3) Kẻ BH vuông góc với AD ở H. Tính AH.Bài 2 : Cho tam giác ABC cân tại A có các đường phân giác BE và CF. Chứng minh :1) Tam giác AEF cân tại A2) Tứ giác BCEF là hình thang cân3) CEEFFBBài 3 : Tứ giac ABCD có góc Agóc B, BCCD và DB là tia phân giác của góc D. Chứng minh:1) Tứ giác ABCD là hình thang vuông2) AC^2 + AD^2 BC^...
Đọc tiếp
Bài 1 : Cho hình thang cân ABCD (AD // BC) có góc A = 60 độ , AD = 4 cm và BC = 2 cm. Qua B kẻ đường thẳng song song với CD cắt AD ở E.
1) Tính ED.
2) Chứng minh tam giác ABE đều.
3) Kẻ BH vuông góc với AD ở H. Tính AH.
Bài 2 : Cho tam giác ABC cân tại A có các đường phân giác BE và CF. Chứng minh :
1) Tam giác AEF cân tại A
2) Tứ giác BCEF là hình thang cân
3) CE=EF=FB
Bài 3 : Tứ giac ABCD có góc A=góc B, BC=CD và DB là tia phân giác của góc D. Chứng minh:
1) Tứ giác ABCD là hình thang vuông
2) AC^2 + AD^2 = BC^2 + BD^2
Bài 4 :Cho hình tang cân ABCD (AB song song CD,AB<CD) có AH,BK là các đường cao. Chứng minh :
1) Tam giác AHD=Tam giác BKC
2) DH = (CD-AB)/2
GIÚP TUI VS!!!! CÂN GẤP Ạ
Bài 2:
a: Xét ΔABE và ΔACF có
góc ABE=góc ACF
AB=AC
góc A chung
Do đó: ΔABE=ΔACF
Suy ra: AE=AF
b: Xét ΔABC có AF/AB=AE/AC
nên FE//BC
=>BFEC là hình thang
mà CF=BE
nên BFEC là hình thang cân
c: Xét ΔFEB có góc FEB=góc FBE
nên ΔFEB cân tại F
=>FE=FB=EC
Đúng 0
Bình luận (0)
Cho hình thang ABCD có AB song song CD. AB=a;BC=b;CD=c,AD=d(d<c) tia phân giác trong của góc A và D cắt nhau tại M.Tia phân giác ngoài góc B và C cắt nhau ở N.
1)CM: MN song song AB
2)Tính MN theo AB;CD
1) Cho hình thang ABCD (AB//CD), I là trung điểm của BD, kéo dài về phía B, M và N theo thứ tự là trung điểm của AB, CD. Gọi E là giao điểm của AB, CD; F là giao điểm IN và BC. CM:a) EF//ABb)MN là phân giác góc ENF nếu ABCD là hình thang cân2) Cho tam giác ABC, đường thẳng song song với trung tuyến AD, vẽ điểm P trên BC cắt AB và AC tại M và N. So sánh AM/AB và AN/AC. Tính tỉ số PM/AD. Cm PN+PM2DA
Đọc tiếp
1) Cho hình thang ABCD (AB//CD), I là trung điểm của BD, kéo dài về phía B, M và N theo thứ tự là trung điểm của AB, CD. Gọi E là giao điểm của AB, CD; F là giao điểm IN và BC. CM:
a) EF//AB
b)MN là phân giác góc ENF nếu ABCD là hình thang cân
2) Cho tam giác ABC, đường thẳng song song với trung tuyến AD, vẽ điểm P trên BC cắt AB và AC tại M và N. So sánh AM/AB và AN/AC. Tính tỉ số PM/AD. Cm PN+PM=2DA
Cho hình thang cân ABCD có AB song song với CD và ab<cd
biết ad=bc
a) cm ab=bc
b) cm db là phân giác adc
Đề bài phải sửa thành "biết AD=AB" mới làm được
a/
ABCD là hình thàng cân => AD=BC
Mà AD=AB (gt)
=> AD=BC
b/
ABCD là hình thang cân
\(\Rightarrow\widehat{BAD}=\widehat{ABC}\)
\(\widehat{BCD}+\widehat{ABC}=180^o\) (Hai góc trong cùng phía)
\(\Rightarrow\widehat{BCD}+\widehat{BAD}=180^o\)
=> ABCD là tứ giác nội tiếp (Tứ giác có tổng 2 góc đối bù nhau là tứ giác nt)
Ta có
Cung AB và cung BC có hai dây trương cung bằng nhau
AB=BC (cmt) => sđ cung AB = sđ cung BC (1)
\(sđ\widehat{ADB}=\dfrac{1}{2}sđcungAB\) (góc nội tiếp) (2)
\(sđ\widehat{CDB}=\dfrac{1}{2}sđcungBC\) (góc nội tiếp) (3)
Từ (1) (2) (3) \(\Rightarrow\widehat{ADB}=\widehat{CDB}\) => DB là phân giác của \(\widehat{ADC}\)
Đúng 0
Bình luận (0)
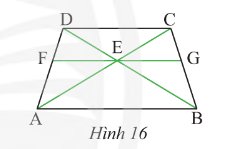
Cho hình thang cân \(ABCD\) có \(AB\) // \(CD\). Qua gia điểm \(E\) của \(AC\) và \(BD\), ta vẽ đường thẳng song song với \(AB\) và cắt \(AD\), \(BC\) lần lượt tại \(F\) và \(G\) (Hình 16). Chứng minh rằng \(EG\) là tia phân giác của góc \(CEB\).
Vì \(EG\) // \(AB\) (gt)
suy ra \(\widehat {{\rm{CEG}}} = \widehat {{\rm{CAB}}}\) (đồng vị) và \(\widehat {{\rm{GEB}}} = \widehat {{\rm{EBA}}}\) (1)
Xét \(\Delta CAB\) và \(\Delta DBA\) ta có:
\(AC = BD\) (tính chất hình thang cân)
\(BC = AD\) (tính chất hình thang cân)
\(AB\) chung
Suy ra \(\Delta CAB = \Delta DBA\) (c-c-c)
Suy ra \(\widehat {{\rm{CAB}}} = \widehat {{\rm{EAB}}}\) (2)
Từ (1) và (2) suy ra \(\widehat {{\rm{CEG}}} = \widehat {{\rm{GEB}}}\)
Suy ra \(EG\) là phân giác của \(\widehat {{\rm{CEB}}}\)
Đúng 0
Bình luận (0)
1, Cho tứ giác ABCD có góc A = góc C = 90 độ. Tia phân giác góc B cắt AD tại E. Qua D kẻ đường thẳng song song BE ,cắt BC tại F . CMR DF là phân giác góc D.
2. Cho hình thang ABCD, góc A = góc B = 90 độ , AB = BC =1/2 AD = 3 cm .
a, tính các góc hình thang
b, AC vuông góc CD
c, tính chu vi hình thang
ai nhanh mình tik cho :3
thông não dùm mình nhé :v



