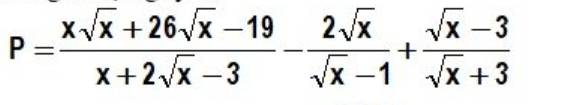
a.rút gọn
b,Với giá trị nào của x thì P đạt giá trị nhỏ nhất và tính giá trị nhỏ nhất đó
LT
Những câu hỏi liên quan
Với giá trị nào của x và y thì tổng S = /x+y/ +2 x /y-2/ +1998 đạt giá trị nhỏ nhất? Tìm giá trị nhỏ nhất đó
dấu / là giá trị tuyệt đối
Với giá trị nào của x, y thì biểu thức: A = /x - y/ + /x + 1/ + 2016 đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó.
Với giá trị nào của x,y thì biểu thức : A=|x-y|+|x+1|+2016 đạt giá trị nhỏ nhất.Tìm giá trị nhỏ nhất đó
Vì |x-y| \(\ge\)0 với mọi x,y;|x+1|\(\ge\)0 vs mọi x
=>A\(\ge\)2016 vs mọi x,y
=> A đạt giá trị nhỏ nhất khi:\(\hept{\begin{cases}\left|x-y\right|=0\\\left|x+1\right|=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x-y=0\\x+1=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=y\\x=-1\end{cases}}\)
vậy với x=y=-1 thì A đạt giá trị nhỏ nhất là 2016
k mik nha
bài này mik từng làm rồi
-----Chúc hok tốt---------
Đúng 0
Bình luận (0)
A = 2018 + \(\sqrt{2018-X}\)
a) Với giá trị nào của x thì A có nghĩa?
b) Với giá trị nào của x thì A đạt giá trị nhỏ nhất? Tìm giá trị nhỏ nhất đó
a) Để \(2018+\sqrt{2018-x}\) thì \(\sqrt{2018-x}\ge0\Leftrightarrow x\le2018\)
b) Để A đạt giá trị nhỏ nhất thì \(\sqrt{2018-x}\) nhỏ nhất. Mà \(\sqrt{2018-x}\ge0\) nên
\(A=2018+\sqrt{2018-x}\ge2018\)
Vậy \(A_{min}=2018\Leftrightarrow\sqrt{2018-x}=0\Leftrightarrow x=2018\)
Đúng 0
Bình luận (0)
Với giá trị nào của x, y thì biểu thức A=\(|x-y|+|x+1|+2011\)đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó
Giá trị nhỏ nhất của A là 2011 (vì A đạt giá trị nhỏ nhất khi /x-y/ + /x+1/ đạt giá trị nhỏ nhất hay bằng 0)
Đúng 0
Bình luận (0)
bằng 2011 là giá trị nhỏ nhất
kết bạn với mình nhé!!!
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Với giá trị nào của x và y thì tổng S= /x+y/+ 2./y-2/+ 1998 đạt giá trị nhỏ nhất?
Tìm giá trị nhỏ nhất đó
Cách làm và lời giải nữa nha bạn
Cho A = \(2013+\sqrt{2012-x}\)
Với giá trị nào của x thì A đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó.
1. với giá trị nào của x thì A=lx-3l + lx-5l + lx-7l đạt giá trị nhỏ nhất ?
2. với giá trị nào của x thì B= lx-1l + lx-2l + lx-3l + lx-5l đạt giá trị nhỏ nhất ?
Bài 1:
\(A=\left|x-3\right|+\left|x-5\right|+\left|x-7\right|\)
\(\ge x-3+0+7-x=4\)
Dấu = khi \(\begin{cases}x-3\ge0\\x-5=0\\7-x\le0\end{cases}\)\(\Leftrightarrow\begin{cases}x\ge3\\x=5\\x\le7\end{cases}\)\(\Leftrightarrow x=5\)
Vậy MinA=4 khi x=5
Bài 2:
\(B=\left|x-1\right|+\left|x-2\right|+\left|x-3\right|+\left|x-5\right|\)
\(\ge x-1+x-2+3-x+5-x=5\)
Dấu = khi \(\begin{cases}x-1\ge0\\x-2\ge0\\3-x\ge0\\5-x\ge0\end{cases}\)\(\Leftrightarrow\begin{cases}x\ge1\\x\ge2\\x\le3\\x\le5\end{cases}\)\(\Leftrightarrow2\le x\le3\)
Đúng 0
Bình luận (0)
Cho biểu thức M = a2 + ab + b2 – 3a – 3b + 2001. Với giá trị nào của a và b thì M đạt giá trị nhỏ nhất? Tìm giá trị nhỏ nhất đó.
\(M=a^2+ab+b^2-3a-3b+2001\)
\(\Rightarrow2M=2a^2+2ab+2b^2-6a-6b+4002\)
\(=\left[\left(a+b\right)^2-2\left(a+b\right).2+4\right]+\left(a^2-2a+1\right)+\left(b^2-2b+1\right)+3996\)
\(=\left(a+b-2\right)^2+\left(a-1\right)^2+\left(b-1\right)^2+3996\ge3996\)
\(\Rightarrow M\ge1998\)
\(minM=1998\Leftrightarrow a=b=1\)
Đúng 2
Bình luận (1)



