x4-2xy6
MJ
Những câu hỏi liên quan
(x2-1/x2):(x2+1/x2) =a tinhsd (x4-1/x4):(x4-1/x4)
Giả sử tồn tại giá trị
x
4
sao cho
x
4
x
3
x
2
x
1
(
x
4...
Đọc tiếp
Giả sử tồn tại giá trị x 4 sao cho x 4 = x 3 = x 2 = x 1 ( x 4 > 0 , x 4 ∈ ℝ ) . Tìm chính xác giá trị của x 4 biết bán kính mặt cầu ngoại tiếp tứ diện CDEF trong trường hợp này là R = 179 20 ?
A. x 4 = 1
B. x 4 = 1 2
C. x 4 = 17
D. x 4 = 5
Đáp án A
R = I C = x 4 179 20
⇒ x 4 = 1
Đúng 0
Bình luận (0)
cho x1, x2, x3, x4, x5 thuộc tập hợp số nguyên
biết x1 + x2 + x3 + x4 + x5=0 và x1+ x2 = x3+ x4 = x4+ x5=2
tính x3, x4, x5
Tìm giá trị của m để bất phương trình
1
-
x
4
+
1
+
x
4
+
x
4
-
2
x
2
≤
m
nghiệm đúng với
∀
m
∈
-
1
;...
Đọc tiếp
Tìm giá trị của m để bất phương trình 1 - x 4 + 1 + x 4 + x 4 - 2 x 2 ≤ m nghiệm đúng với ∀ m ∈ - 1 ; 1
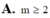
![]()
![]()
![]()
Cho bốn số x1, x2, x3, x4 khác 0 thỏa mãn x22 = x1.x3 ; x23 = x2.x4 Chứng minh rằng: x1/ x4 = (x1 x2 x3 / x2 x3 x4 ) ^3
Cho x1 ,x2, x3 , x4 , x5 thuộc z.
Biết x1+x2=x3+x4=x4+x5=2 và
Tất cả 5 số cộng lại = 0
Tính x5 , x4 và x3
giải
ta có :
\(x1+x2+x3+x4+x5=0\)
\(\left(x1+x2\right)+\left(x3+x4\right)+x5=0\)
\(\Rightarrow2+2+x5=0\Rightarrow x5=-4\)
mà \(x4+x5=2\Rightarrow x4+-4=2\Rightarrow x4=6\)
mặt khác : \(x3+x4=2\Rightarrow x3+6=2\Rightarrow x3=-4\)
vậy : x5 = -4 , x4 = 6 , x3 = -4
Ta có : \(\left\{{}\begin{matrix}x_1+x_2=2\left(I\right)\\x_3+x_4=2\left(II\right)\\x_4+x_5=2\left(III\right)\\x_1+x_2+x_3+x_4+x_5=5\left(IV\right)\end{matrix}\right.\)
Thay (I) và (II) vào (IV) ta được : 2+2+x5=5 => x5=1
Thay x5=1 vào (III) ta được: x4=1
Thay x4=1 vào (II) ta được: x3=1
Vậy x3=x4=x5=1
phân tích đa thức thành nhân tử
a) x4+\(\dfrac{1}{4}\)y8
b) \(\dfrac{1}{4}\)x4+y8
c) 64x4+y4
d) x4+\(\dfrac{1}{64}\)y4
Lời giải:
a.
$=(x^2)^2+(\frac{1}{2}y^4)^2+2.x^2.\frac{1}{2}y^4-x^2y^4$
$=(x^2+\frac{1}{2}y^4)^2-(xy^2)^2$
$=(x^2+\frac{1}{2}y^4-xy^2)(x^2+\frac{1}{2}y^4+xy^2)$
b.
$=(\frac{1}{2}x^2)^2+(y^4)^2+2.\frac{1}{2}x^2.y^4-x^2y^4$
$=(\frac{1}{2}x^2+y^4)^2-(xy^2)^2$
$=(\frac{1}{2}x^2+y^4-xy^2)(\frac{1}{2}x^2+y^4+xy^2)$
c.
$=(8x^2)^2+(y^2)^2+2.8x^2.y^2-16x^2y^2$
$=(8x^2+y^2)^2-(4xy)^2=(8x^2+y^2-4xy)(8x^2+y^2+4xy)$
d.
$=\frac{64x^4+y^4}{64}=\frac{1}{64}(8x^2+y^2-4xy)(8x^2+y^2+4xy)$
Đúng 1
Bình luận (0)
c: \(64x^4+y^4\)
\(=64x^4+16x^2y^2+y^4-16x^2y^2\)
\(=\left(8x^2+y^2\right)^2-\left(4xy\right)^2\)
\(=\left(8x^2+y^2-4xy\right)\left(8x^2+y^2+4xy\right)\)
Đúng 0
Bình luận (0)
TỊM x1+x2+x3+x4+x5+xx6
x1+x2=x3+x4=x5+x6=2bieestx1+x2+x3+x4+X5+x6=0
Phân tích các đa thức sau thành nhân tử
a,x4+2x3+3x2+2x+1
b,x4-4x3+2x2+4x+1
c,x4+x3+2x2+2x+4



