Từ đó xác định ước của các số trên 34;52;145;370
TA
Những câu hỏi liên quan
phân tích các số sau ra thừa số nguyên tố , tìm ước của số đó và xác định các ước của nó
16=24
Số ước của 16 là: (4+1)*2=10(ước)
Ư(16)={1;-1;2;-2;4;-4;8;-8;16;-16}
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
một nguyên tử nguyên tố a có tổng số các loại hạt trong nguyên tử là 34,trong đó số hạt mang điện tích nhiều hơn hạt ko mang điện tích là 10.xác định số lượng mỗi loại hạt,từ đó xác định tên và kí hiệu hóa học của nguyên tử nguyên tố đó
`#3107.101107`
Gọi các hạt trong nguyên tử là `p, n, e`
Tổng số hạt trong nguyên tử là `34`
`=> p + n + e = 34`
Mà trong nguyên tử, số `p = e`
`=> 2p + n = 34`
Số hạt mang điện nhiều hơn số hạt không mang điện
`=> 2p - n = 10 => n = 2p - 10`
`=> 2p + 2p - 10 = 34`
`=> 4p = 34 + 10`
`=> 4p = 44`
`=> p = 11 => p = e = 11`
Số hạt n có trong nguyên tử là: `34 - 11 - 11 = 12`
- Tên của nguyên tử nguyên tố a: Sodium (Natri)
- KHHH: Na.
Đúng 3
Bình luận (0)
một nguyên tử nguyên tố A có tổng số các loại hạt trong nguyên tử là 34 trong số hạt mang điện nhiều hơn số hạt không mang điện là 10.Xác định số lượng mỗi loại hạt,từ đó xác định tên và kí hiệu hóa học của 1 số nguyên tố sau: CA,CALI,CU,FE Giúp mình với ạ
Đúng 0
Bình luận (0)
Bài tập 1. Cho hai tập hợp A{ số tự nhiên là ước của 12} và B {x | x là số nguyên tố nhỏ hơn 10} : a. Xác định các phần tử của tập hợp A{..}, B {..} b. Xác định các phần tử của tập hợp A U Bc. Xác định tập hợp AB{..}d. Xác định BA {...}e. Xác định các phần tử của tập hợp A x B {...} Bài tập 2. Chứng minh rằng : từ tập tích đề các A x A nếu xác định tập hợp con S ( gồm có các cặp số ( n;n) , trong đó n thuộc A thì ta được quan hệ tương đương trên A
Đọc tiếp
Bài tập 1. Cho hai tập hợp A={ số tự nhiên là ước của 12} và B ={x | x là số nguyên tố nhỏ hơn 10} :
a. Xác định các phần tử của tập hợp A={..}, B ={..}
b. Xác định các phần tử của tập hợp A U B
c. Xác định tập hợp A\B={..}
d. Xác định B\A ={...}
e. Xác định các phần tử của tập hợp A x B ={...}
Bài tập 2. Chứng minh rằng : từ tập tích đề các A x A nếu xác định tập hợp con S = ( gồm có các cặp số ( n;n) , trong đó n thuộc A thì ta được quan hệ tương đương trên A
Phân tích các số sau ra thừa số nguyên tố Tìm số ước của số đó và xác định các ước của nó a)9 ; b)16 ; c) 27 ; d)18 ; e)45 ; f)63 ; g)120 ; h)210
Phát biểu quy ước về tập xác định của một hàm số cho bởi công thức.
Từ đó hai hàm số
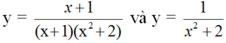
có gì khác nhau?
- Tập xác định của hàm số cho bởi công thức y = f(x) là tập hợp các giá trị của x sao cho biểu thức f(x) có nghĩa.
- Với quy ước đó:
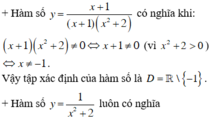
Vậy tập xác định của hàm số là D = R
Kết luận: Hai hàm số 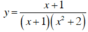 và
và 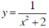 có tập xác định khác nhau.
có tập xác định khác nhau.
Đúng 0
Bình luận (0)
cho số tự nhiên p= a^xb^y trong đó a,b là các số nguyên tố khác nhau;x,y là các số tự nhiên khác 0.Biết p^2 có đúng 15 ước số,hãy xác định số ước số của p^3.
Cho lúa hạt dài lai với lúa hạt tròn, F1 thu được toàn lúa hạt dài. Xác định tính trội, lặn ?(biết các tính trạng di truyền theo quy luật Mendel)Quy định gen (quy ước gen) của cặp tính trạng trên? *Xác định kiểu gen của cặp tính trạng trên? *Xác định kiểu gen, kiểu hình F1? *Xác định kiểu gen của F1? *Cho F1 x F1, , F2 có kết quả như thế nào? * Giúp e với ạ 9h e nộp rồi ạ. Cảm ơn mọi người :3
Đọc tiếp
Cho lúa hạt dài lai với lúa hạt tròn, F1 thu được toàn lúa hạt dài. Xác định tính trội, lặn ?(biết các tính trạng di truyền theo quy luật Mendel)
Quy định gen (quy ước gen) của cặp tính trạng trên? *
Xác định kiểu gen của cặp tính trạng trên? *
Xác định kiểu gen, kiểu hình F1? *
Xác định kiểu gen của F1? *
Cho F1 x F1, , F2 có kết quả như thế nào? *
Giúp e với ạ 9h e nộp rồi ạ. Cảm ơn mọi người :3
Do lai lúa hạt dài với lúa hạt ngắn thu dc F1 toàn lúa hạt dài
=> Hạt dài THT so với hạt ngắn
Quy ước gen: A hạt dài. a hạt ngắn
vì cho lai hạt dài với hạt ngắn => F1 nhận 2 loại giao tử: A,a
=> kiểu gen F1: Aa
F1 dị hợp => P thuần chủng.
kiểu genP: AA x aa
P(t/c). AA( hạt dài). x. aa( hạt ngắn)
Gp. A. a
F1. Aa(100% hạt dài)
F1xF1. Aa( hạt dài). x. Aa( hạt dài)
GF1. A,a. A,a
F2: 1AA:2Aa:1aa
kiểu hình:3 lúa hạt dài:1 lúa hạt ngắn
Đúng 2
Bình luận (0)
lai lúa hạt dài với lúa hạt ngắn thu dc F1 toàn lúa hạt dài
=> Hạt dài THT so với hạt ngắn
Quy ước gen: A hạt dài. a hạt ngắn
vì cho lai hạt dài với hạt ngắn => F1 nhận 2 loại giao tử: A,a
=> kiểu gen F1: Aa
F1 dị hợp => P thuần chủng.
kiểu genP: AA x aa
P(t/c). AA( hạt dài). x. aa( hạt ngắn)
Gp. A. a
F1. Aa(100% hạt dài)
F1xF1. Aa( hạt dài). x. Aa( hạt dài)
GF1. A,a. A,a
F2: 1AA:2Aa:1aa
kiểu hình:3 lúa hạt dài:1 lúa hạt ngắn
Đúng 0
Bình luận (0)
nguyên tử của một nguyên tố có tổng số các hạt là 34 , trong đó số hạt mang điẹn nhiều hơn số hạt không mang điện là 10 . Xác định số proton , neutron , electron của nguyên tố đó
Ta có: P + N + E = 34
Mà: P = E (do nguyên tử trung hòa về điện)
⇒ 2P + N = 34 (1)
Theo đề, số hạt mang điện nhiều hơn số hạt không mang điện là 10.
⇒ 2P - N = 10 (2)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}P=E=11\\N=12\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Nguyên tử của một nguyên tố có tổng số các loại hạt là 34 trong đó số hạt không mạng điện là 12.Xác định số p,số n,số e của nguyên tử nguyên tố đó
Giúp e với
Ta có:
\(\left\{{}\begin{matrix}p+e+n=34\\n=12\end{matrix}\right.\)
mà \(p=e\) (trung hòa về điện)
\(\Rightarrow2p+n=34\\ \Rightarrow2p+12=34\\ \Rightarrow p=e=11\)
Đúng 2
Bình luận (0)
Ta có: \(p+e+n=34\) Mà số p = số e
\(\Rightarrow\) \(2p+n=34\left(1\right)\)
Ta lại có: \(2p-n=12\left(2\right)\)
Từ ( 1 ) và ( 2 ) ta có hệ phương trình sau:
\(\left\{{}\begin{matrix}2p+n=34\\2p-n=12\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}p=12,e=12\\n=11\end{matrix}\right.\)
( 12 là xấp xỉ làm tròn của 11,5 nha )
Đúng 1
Bình luận (1)
Xem thêm câu trả lời





