a, Áp dụng các hệ thức lượng trong tam giác vuông ABD, tính được BD = 25cm, OB = 9cm, OD = 16cm

b, Áp dụng các hệ thức lượng trong tam giác vuông DAC tính được OA = 12cm, AC = 100 3 cm

c, Tính được S =  1250 3 c m 2

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:

\(BC^2=AB^2+AC^2\)

\(\Leftrightarrow BC^2=6^2+8^2=100\)

hay BC=10(cm)

Vậy: BC=10cm

a) Xét ΔABC có 

BD là đường phân giác ứng với cạnh AC(gt)

nên \(\dfrac{AD}{AB}=\dfrac{CD}{BC}\)(Tính chất tia phân giác của tam giác)

hay \(\dfrac{AD}{6}=\dfrac{CD}{10}\)

mà AD+CD=AC=8(cm)(D nằm giữa A và C)

nên Áp dụng tính chất của dãy tỉ số bằng nhau,ta được:

\(\dfrac{AD}{6}=\dfrac{CD}{10}=\dfrac{AD+CD}{6+10}=\dfrac{8}{16}=\dfrac{1}{2}\)

Do đó:

\(\left\{{}\begin{matrix}\dfrac{AD}{6}=\dfrac{1}{2}\\\dfrac{CD}{10}=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AD=3\left(cm\right)\\CD=5\left(cm\right)\end{matrix}\right.\)

Vậy: AD=3cm; CD=5cm

b) Xét ΔABD vuông tại A và ΔHBI vuông tại H có 

\(\widehat{ABD}=\widehat{HBI}\)(BI là tia phân giác của \(\widehat{ABH}\))

Do đó: ΔABD\(\sim\)ΔHBI(g-g)

a) Vẽ hình chữ nhật ABCD có chiều dài 4 cm, chiều rộng 3 cm. Sau đó nối đỉnh A với đỉnh C, đỉnh B, đỉnh D.

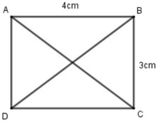
b) Đo chiều dài đoạn thẳng

AC, BD rồi viết số thích hợp vào chỗ chấm:

- AC = 5 cm

- BD = 5 cm

c) Nhận xét:

Độ dài AC = độ dài BD

(AC, BD là hai đường chéo của hình chữ nhật)

a: Xét ΔBDC vuông tại B và ΔHBC vuông tại H có

góc C chung

Do đo: ΔBDC\(\sim\)ΔHBC

b: \(BD=\sqrt{10^2-6^2}=8\left(cm\right)\)

\(HC=\dfrac{BC^2}{CD}=\dfrac{6^2}{10}=3.6\left(cm\right)\)

HD=10-3,6=6,4(cm)

Bài 1 : 

Vì ABCD là hình vuông \(\Rightarrow\widehat{DAB}=\widehat{ABC}=\widehat{BCD}=\widehat{CDA}=90^0\)

\(\Rightarrow AB=BC=CD=AD=4\)cm 

Áp dụng định lí pytago tam giác ADC vuông tại D ta có : 

\(AC^2=AD^2+CD^2=16+16=32\Rightarrow AC=4\sqrt{2}\)cm 

Vì ABCD là hình vuông nên 2 đường chéo bằng nhau AC = BD = 4\(\sqrt{2}\)cm 

Bài 2 : 

Vì ABCD là hình chữ nhật nên \(AB=CD;AD=BC\)

Áp dụng định lí Pytago tam giác ACD vuông tại D ta có :

 \(AC^2=AD^2+DC^2=27+9=36\Rightarrow AC=6\)cm 

Bài 3 : 

Áp dụng định lí Pytago cho tam giác ABH vuông tại H ta có : 

\(AB^2=BH^2+AH^2=16+36=52\Rightarrow AB=2\sqrt{13}\)cm 

Áp dụng định lí Pytago cho tam giác ACH vuông tại H ta có : 

\(AC^2=CH^2+AH^2=81+36=117\Rightarrow AC=3\sqrt{13}\)cm 

\(BC=CH+BH=9+4=13\)cm