Cho tam giác ABC,\(\widehat{A}=120^o,\widehat{B}=35^o,AB=12.25cm\)Giải tam giác ABC
NP
Những câu hỏi liên quan
Giải tam giác ABC trong các trường hợp sau:
a) \(AB = 14,AC = 23,\widehat A = {125^o}.\)
b) \(BC = 22,4;\widehat B = {64^o};\widehat C = {38^o}.\)
c) \(AC = 22,\widehat B = {120^o},\widehat C = {28^o}.\)
d) \(AB = 23,AC = 32,BC = 44\)
a) Ta cần tính cạnh BC và hai góc \(\widehat B,\widehat C.\)
Áp dụng định lí cosin, ta có:
\(\begin{array}{l}B{C^2} = A{B^2} + A{C^2} - 2.AB.AC.\cos A\\ \Leftrightarrow B{C^2} = {14^2} + {23^2} - 2.14.23.\cos {125^o}\\ \Rightarrow BC \approx 33\end{array}\)
Áp dụng định lí sin, ta có:
\(\begin{array}{l}\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}} \Leftrightarrow \frac{{33}}{{\sin {{125}^o}}} = \frac{{23}}{{\sin B}} = \frac{{14}}{{\sin C}}\\ \Rightarrow \sin B = \frac{{23.\sin {{125}^o}}}{{33}} \approx 0,57\\ \Rightarrow \widehat B \approx {35^o} \Rightarrow \widehat C \approx {20^o}\end{array}\)
b) Ta cần tính góc A và hai cạnh AB, AC.
Ta có: \(\widehat A = {180^o} - \widehat B - \widehat C = {180^o} - {64^o} - {38^o} = {78^o}\)
Áp dụng định lí sin, ta có:
\(\begin{array}{l}\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}} \Leftrightarrow \frac{{22}}{{\sin {{78}^o}}} = \frac{{AC}}{{\sin {{64}^o}}} = \frac{{AB}}{{\sin {{38}^o}}}\\ \Rightarrow \left\{ \begin{array}{l}AC = \sin {64^o}.\frac{{22}}{{\sin {{78}^o}}} \approx 20,22\\AB = \sin {38^o}.\frac{{22}}{{\sin {{78}^o}}} \approx 13,85\end{array} \right.\end{array}\)
c) Ta cần tính góc A và hai cạnh AB, BC.
Ta có: \(\widehat A = {180^o} - \widehat B - \widehat C = {180^o} - {120^o} - {28^o} = {32^o}\)
Áp dụng định lí sin, ta có:
\(\begin{array}{l}\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}} \Leftrightarrow \frac{{BC}}{{\sin {{32}^o}}} = \frac{{22}}{{\sin {{120}^o}}} = \frac{{AB}}{{\sin {{28}^o}}}\\ \Rightarrow \left\{ \begin{array}{l}BC = \sin {32^o}.\frac{{22}}{{\sin {{120}^o}}} \approx 13,5\\AB = \sin {28^o}.\frac{{22}}{{\sin {{120}^o}}} \approx 12\end{array} \right.\end{array}\)
d) Ta cần tính số đo ba góc \(\widehat A,\widehat B,\widehat C\)
Áp dụng hệ quả của định lí cosin, ta có:
\(\begin{array}{l}\cos A = \frac{{A{C^2} + A{B^2} - B{C^2}}}{{2.AB.AC}};\cos B = \frac{{B{C^2} + A{B^2} - A{C^2}}}{{2.BC.BA}}\\ \Rightarrow \cos A = \frac{{{{32}^2} + {{23}^2} - {{44}^2}}}{{2.32.23}} = \frac{{ - 383}}{{1472}};\cos B = \frac{{{{44}^2} + {{23}^2} - {{32}^2}}}{{2.44.23}} = \frac{{131}}{{184}}\\ \Rightarrow \widehat A \approx {105^o},\widehat B = {44^o}36'\\ \Rightarrow \widehat C = {30^o}24'\end{array}\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB = 12; \(\widehat B = {60^o}\); \(\widehat C = {45^o}\). Tính diện tích của tam giác ABC.
Áp dụng định lí sin trong tam giác ABC, ta có:
\(\frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}\)
\( \Rightarrow AC = \sin B.\frac{{AB}}{{\sin C}} = \sin {60^o}.\frac{{12}}{{\sin {{45}^o}}} = 6\sqrt 6 \)
Lại có: \(\widehat A = {180^o} - ({60^o} + {45^o}) = {75^o}\)
\( \Rightarrow \)Diện tích tam giác ABC là:
\(S = \frac{1}{2}AB.AC.\sin A = \frac{1}{2}.12.6\sqrt 6 .\sin {75^o} \approx 85,2\)
Vậy diện tích tam giác ABC là 85,2.
Đúng 0
Bình luận (0)
5. Cho tam giác ABC; 2 đường phân giác AD, BE; với D ϵ BC, E ϵ AC. CMR:
a) \(\widehat{ADC}=\widehat{BEC}\) thì \(\widehat{A}=\widehat{B}\).
b) \(\widehat{ADB}=\widehat{BEC}\) thì \(\widehat{A}+\widehat{B}=120^o\).
a) Để chứng minh a) ta cần chứng minh rằng góc ADC bằng góc BEC.
Vì AD là đường phân giác của góc BAC, nên ta có:
∠DAB = ∠DAC (1)
Tương tự, vì BE là đường phân giác của góc ABC, nên ta có:
∠CBA = ∠CBE (2)
Từ (1) và (2), ta có:
∠DAB + ∠CBA = ∠DAC + ∠CBE
∠DAB + ∠CBA = ∠BAC + ∠ABC
∠DAB + ∠CBA = ∠ABC + ∠BAC
Do đó, góc ADC bằng góc BEC.
Tiếp theo, để chứng minh rằng góc A bằng góc B, ta sử dụng định lý phụ của đường phân giác:
∠DAB = ∠DAC
∠EBA = ∠EBC
Vì ∠ADC = ∠BEC (đã chứng minh ở trên), nên ta có:
∠DAC + ∠ADC = ∠DAB + ∠ABC
∠DAB + ∠ABC = ∠DAC + ∠ADC
Từ đây, suy ra ∠A = ∠B.
Vậy, điều phải chứng minh a) đã được chứng minh.
b) Để chứng minh b), ta cần chứng minh rằng góc ADB bằng góc BEC.
Từ ∠ADB = ∠BEC (đã chứng minh ở a)), ta có:
∠ADB + ∠BEC = ∠BEC + ∠BEC
∠ADB + ∠BEC = 2∠BEC
∠ADB = ∠BEC
Do đó, góc ADB bằng góc BEC.
Tiếp theo, ta có:
∠A + ∠B + ∠C = 180° (định lý tổng các góc trong tam giác)
∠ADB + ∠B + ∠BEC = 180°
∠BEC + ∠B + ∠BEC = 180° (vì ∠ADB = ∠BEC)
2∠BEC + ∠B = 180°
2∠BEC = 180° - ∠B
∠BEC = (180° - ∠B) / 2
∠BEC = 90° - ∠B/2
∠BEC = 90° - ∠A/2 (vì ∠A = ∠B)
∠A/2 + ∠B/2 + ∠C = 90°
∠A/2 + ∠B/2 + ∠C = 90° - ∠A/2
∠A/2 + ∠A/2 + ∠C = 90° - ∠A/2
∠A + ∠C = 90° - ∠A/2
∠A + ∠C + ∠A/2 = 90°
2∠A + ∠C = 180°
∠A + ∠C = 180° - ∠A
∠A + ∠C = ∠B
∠A + ∠B + ∠C = 180°
∠A + ∠B + ∠C = 120° + 60°
∠A + ∠B + ∠C = 180°
Do đó, ∠A + ∠B = 120°.
Vậy, điều phải chứng minh b) đã được chứng minh.
Đúng 0
Bình luận (0)
Cho tam tam giác ABC có các góc nhọn < \(120^o\). Vẽ ở phía ngoài tam giác ABC các tam giác đều ABD, ACE. Gọi M là giao điểm của DC và BE. CMR:
a, \(\widehat{BMC}=120^o\)
b. \(\widehat{AMB}=120^o\)
Cho tam giác ABC có \(AB = 100,\widehat B = {100^o},\widehat C = {45^o}.\) Tính:
a) Độ dài các cạnh AC, BC
b) Diện tích tam giác ABC.
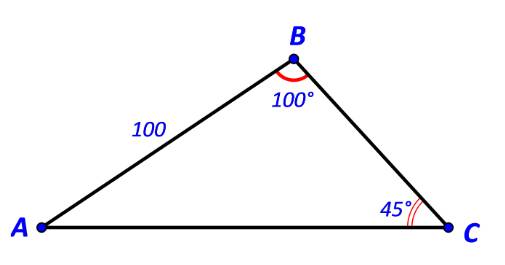
a)
Ta có: \(\widehat A = {180^o} - (\widehat B + \widehat C)\) \( \Rightarrow \widehat A = {180^o} - ({100^o} + {45^o}) = {35^o}\)
Áp dụng định lí sin trong tam giác ABC ta có:
\(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}} = \frac{{BC}}{{\sin A}}\)
\( \Rightarrow \left\{ \begin{array}{l}AC = \sin B.\frac{{AB}}{{\sin C}}\\BC = \sin A.\frac{{AB}}{{\sin C}}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}AC = \sin {100^o}.\frac{{100}}{{\sin {{45}^o}}} \approx 139,3\\BC = \sin {35^o}.\frac{{100}}{{\sin {{45}^o}}} \approx 81,1\end{array} \right.\)
b)
Diện tích tam giác ABC là: \(S = \frac{1}{2}.BC.AC.\sin C = \frac{1}{2}.81,1.139,3.\sin {45^o} \approx 3994,2.\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có \(AB = 5,BC = 7,\widehat A = {120^o}.\) Tính độ dài cạnh AC.
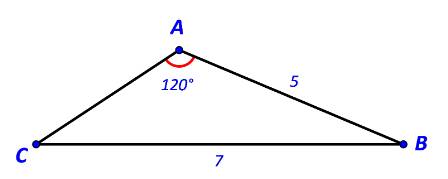
Áp dụng định lí sin trong tam giác ABC ta có:
\(\frac{{AB}}{{\sin C}} = \frac{{BC}}{{\sin A}}\)
\( \Rightarrow \sin C = \sin A.\frac{{AB}}{{BC}} = \sin {120^o}.\frac{5}{7} = \frac{{5\sqrt 3 }}{{14}}\)
\( \Rightarrow \widehat C \approx 38,{2^o}\) hoặc \(\widehat C \approx 141,{8^o}\) (Loại)
Ta có: \(\widehat A = {120^o},\widehat C = 38,{2^o}\)\( \Rightarrow \widehat B = {180^o} - \left( {{{120}^o} + 38,{2^o}} \right) = 21,{8^o}\)
Áp dụng định lí cosin trong tam giác ABC ta có:
\(\begin{array}{l}A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos B\\ \Leftrightarrow A{C^2} = {5^2} + {7^2} - 2.5.7.\cos 21,{8^o}\\ \Rightarrow A{C^2} \approx 9\\ \Rightarrow AC = 3\end{array}\)
Vậy độ dài cạnh AC là 3.
Đúng 0
Bình luận (0)
Giải tam giác ABC và tính diện tích của tam giác đó, biết \(\widehat A = {15^o},\;\widehat B = {130^o},\;c = 6\).
Ta có: \(\widehat A = {15^o},\;\widehat B = {130^o} \Rightarrow \widehat C = {35^o}\)
Áp dụng định lí sin trong tam giác ABC ta có:
\(\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}}\)
\( \Rightarrow b = \dfrac{{c.\sin B}}{{\sin C}};\;\;a = \dfrac{{c.\sin A}}{{\sin C}}\)
Mà \(\widehat A = {15^o},\;\widehat B = {130^o},\;\widehat C = {35^o},c = 6\)
\( \Rightarrow b = \dfrac{{6.\sin {{130}^o}}}{{\sin {{35}^o}}} \approx 8;\;\;a = \dfrac{{6.\sin {{15}^o}}}{{\sin {{35}^o}}} \approx 2,7\)
Diện tích tam giác ABC là \(S = \dfrac{1}{2}bc.\sin A = \dfrac{1}{2}.8.6.\sin {15^o} \approx 6,212.\)
Vậy \(a \approx 2,7;\;\,b \approx 8\); \(\widehat C = {35^o}\); \(S \approx 6,212.\)
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, widehat{BAC}120^o, ABACa. Tam giác SAB vuông tại B, tam giác SAC vuông tại C, góc giữa hai mặt phẳng left(SABright) và left(ABCright) bằng 60^o. Gọi H là hình chiếu vuông góc của điểm S lên mặt phẳng left(ABCright). Chứng minh rằng HB vuông góc AB và tính thể tích khối chóp S.ABC theo a
Đọc tiếp
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cân tại \(A\), \(\widehat{BAC}=120^o\), \(AB=AC=a\). Tam giác \(SAB\) vuông tại \(B\), tam giác \(SAC\) vuông tại \(C\), góc giữa hai mặt phẳng \(\left(SAB\right)\) và \(\left(ABC\right)\) bằng \(60^o\). Gọi \(H\) là hình chiếu vuông góc của điểm \(S\) lên mặt phẳng \(\left(ABC\right)\). Chứng minh rằng \(HB\) vuông góc \(AB\) và tính thể tích khối chóp \(S.ABC\) theo \(a\)
Cho tam giác ABC, \(\widehat{A}< 120^o\). Vẽ ra ngoài tam giác ấy các tam giác đều ABD và ACE. Gọi I là giao điểm của BE và CD.
a) Tính \(\widehat{BIC}\)
b) Chứng minh ID = IA + IB
c) Chứng minh \(\widehat{AIB}=\widehat{BIC}=\widehat{AIC=}120^o\)

