Vẽ tam giác đều rồi tô màu như hình bên.

Tạo lập hình chóp tam giác đều có độ dài cạnh đáy 3cm và cạnh bên 4cm theo hướng dẫn sau:
- Trên một tấm bìa, vẽ một hình tam giác đều và ba hình tam giác cân với kích thước như Hình 7a.
- Cắt tấm bìa như hình vẽ, rồi gấp theo các đường màu đỏ ta được hình chóp tam giác đều như Hình 7b.
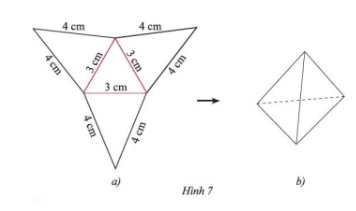
Sau khi thực hiện theo hướng dẫn, ta được sản phẩm như hình 7b.
Tạo lập hình chóp tứ giác đều có độ dài cạnh đáy 4cm và cạnh bên 5cm theo hướng dẫn sau:
- Trên một tấm bìa, vẽ một hình vuông và bốn hình tam giác cân với kích thước như Hình 9a.
- Cắt tấm bìa như hình vẽ, rồi gấp theo các đường màu đỏ ta được hình chóp tứ giác đều như Hình 9b.
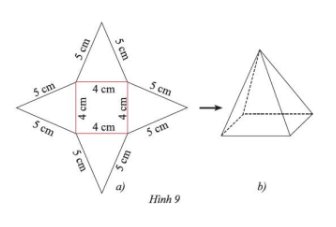
Sau khi thực hiện theo hướng dẫn, ta được sản phẩm như Hình 9b.
a) Viết tiếp tên ba điểm thẳng hàng có trong hình vẽ bên (theo mẫu):
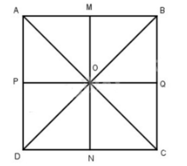
A, O, C
……………………
……………………
……………………
……………………
……………………
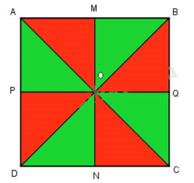
b) Tô màu các hình tam giác trong hình vẽ trên sao cho hai hình tam giác liền kề nhau có màu khác nhau.
Phương pháp giải:
a) Quan sát hình vẽ rồi tìm ba điểm cùng nằm trên một đoạn thẳng và liệt kê theo mẫu.
b) Tô màu các tam giác thỏa mãn điều kiện của bài toán.
Lời giải chi tiết:
a) Viết ba điểm thẳng hàng có trong hình vẽ bên:
A, O, C;
M, O, N;
D, O, B;
A, P, D;
A, M, B;
P, O, Q;
C, Q, B;
D, N, C.
b) Tô màu các hình tam giác trong hình vẽ trên sao cho hai hình tam giác liền kề nhau có màu khác nhau.
Xét một tập hợp gồm các ô trống hình tròn như hình vẽ lập thành tam giác đều có "cạnh \(n\)" như hình vẽ (trong hình thì \(n=6\))
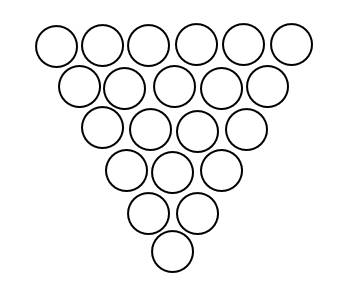
Ta thực hiện trò chơi sau: Ở hàng đầu tiên, mỗi ô hình tròn trong hàng này đều được tô ngẫu nhiên bởi 1 trong 3 màu: xanh, đỏ, vàng. Từ dòng thứ hai trở đi, ta tô màu theo quy tắc sau:
i) Nếu 2 ô liên tiếp ở dòng trên được tô bởi 2 màu khác nhau thì ô trống nằm ngay dưới 2 ô đó được tô bởi màu còn lại.

ii) Nếu 2 ô liên tiếp ở hàng trên được tô bởi cùng 1 màu thì ô trống nằm ngay dưới 2 ô đó cũng được tô bởi màu này.

Cứ tiếp tục như thế cho đến hàng cuối cùng.
a) Với \(n=4,n=10\), CMR màu ở ô trống hàng cuối cùng chính là tổng của 2 màu của 2 ô trống ở góc trên của tam giác đều.
b) Với \(n=6,n=8\) điều này có còn đúng hay không? Vì sao?
c) Tìm tất cả các số tự nhiên \(n\) thỏa mãn điều kiện ở a).
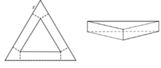
Cắt ba góc của một tam giác đều cạnh a các đoạn bằng x , 0 < x < a 2 phần còn lại là một tam giác đều bên ngoài là các hình chữ nhật, rồi gấp các hình chữ nhật lại tạo thành khối lăng trụ tam giác đều như hình vẽ. Tìm độ dài x để thể tích khối lăng trụ lớn nhất.
A. x = a 3
B. x = a 4
C. x = a 5
D. x = a 6
Đáp án là D.
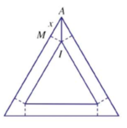
M I = x 3 3 ; S t g = a − 2 x 2 3 4 .
V l t = M I . S t g = a 2 x − 4 a x 2 + 4 x 3 4 ; 0 < x < a 2 .
xét hàm số
f x = 4 x 3 − 4 a x 2 + a 2 x ⇒ f ' x = 12 x 2 − 8 a x + a 2 , cho f ' x = 0 ⇔ x = a 6 x = a 2 l o a i
Thể tích đạt GTLN khi x = a 6 .
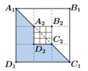
Với hình vuông A 1 B 1 C 1 D 1 như hình vẽ bên, cách tô màu như phần gạch sọc được gọi là cách tô màu đẹp Một nhà thiết kế tiến hành tô màu cho một hình vuông như hình bên, theo quy trình sau:
Bước 1: Tô màu đẹp cho hình vuông A 1 B 1 C 1 D 1 .
Bước 2: Tô màu đẹp cho hình vuông A 2 B 2 C 2 D 2 là hình vuông ở chính giữa khi chia hình vuông A 1 B 1 C 1 D 1 thành 9 phần bằng nhau như hình vẽ.
Bước 3: Tô màu đẹp cho hình vuông A 3 B 3 C 3 D 3 là hình vuông ở chính giữa khi chia hình vuông A 2 B 2 C 2 D 2 thành 9 phần bằng nhau. Cứ tiếp tục như vậy. Hỏi cần ít nhất bao nhiêu bước để tổng diện tích phần được tô màu chiếm 49,99%?
A. 9 bước
B. 4 bước
C. 8 bước
D. 7 bước
Gọi diện tích được tô màu ở mỗi bước là ![]() Dễ thấy dãy các giá trị
u
n
là một cấp số nhân với số hạng đầu
u
1
=
4
9
và công bội q =
1
9
Dễ thấy dãy các giá trị
u
n
là một cấp số nhân với số hạng đầu
u
1
=
4
9
và công bội q =
1
9
Gọi
S
k
là tổng của k số hạng đầu trong cấp số nhân đang xét thì 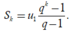
Để tổng diện tích phần được tô màu chiếm 49,99% khi và chỉ khi
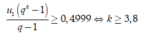
Vậy cần ít nhất 4 bước. Chọn B.
Một tấm bìa hình vuông đã được tô màu như hình vẽ bên.
Tính: Chu vi của phần không tô màu
Chu vi của phần không tô màu là:
10 x 2 x 3,14 = 62,8 (cm)
Một tấm bìa hình vuông đã được tô màu như hình vẽ bên.
Tính: Diện tích của phần đã tô màu.
Ghép 4 mảnh đã tô màu của hình vuông ta được một hình tròn có bán kính là 10cm.
Vậy diện tích phần đã tô màu là:
10 x 10 x 3,14 = 314 (cm2)
Một tấm bìa hình vuông đã được tô màu như hình vẽ bên.
Tính:
a) Diện tích của phần đã tô màu.
b) Chu vi của phần không tô màu.
a) Ghép 4 mảnh đã tô màu của hình vuông ta được một hình tròn có bán kính là 10cm.
Vậy diện tích phần đã tô màu là:
10 x 10 x 3,14 = 314 ( cm 2 )
b) Chu vi của phần không tô màu là:
10 x 2 x 3,14 = 62,8 (cm)
Đáp số: a) 314 cm 2 ;
b) 62,8cm
hehe tui bay giai ko duoc thi lam cho di
Sai rồi sai rồi