Đa giác nào có số đường chéo bằng số cạnh
Đa giác nào có số đường chéo bằng số cạnh?
Đa giác nào dưới đây có số đường chéo bằng số cạnh?
A. Tứ giác
B. Ngũ giác
C. Lục giác
D. Đa giác có 7 cạnh
Gọi số cạnh của đa giác là n (n ≥ 3; n Є N)
Số đường chéo của đa giác là
n ( n − 3 ) 2
Theo đề bài ta có
n ( n − 3 ) 2 = n ó n2 – 3n = 2n
ó n2 – 5n = 0ó n (n – 5) = 0
ó n = 0 ( k t m ) n = 5 ( t m )
Vậy đa giác thỏa mãn đề bài là ngũ giác
Đáp án cần chọn là: B
Một đa giác có số đường chéo bằng số cạnh của đa giác thì đa giác có số cạnh là?
A. 5.
B. 6.
C. 4.
D. 7.
Số đường chéo của đa giác n cạnh là (n( n - 3 ))/2. ( n ∈ N, n ≥ 3 )
Theo giả thiết ta có (n( n - 3 ))/2 = n ⇔ n( n - 3 ) = 2n ⇔ n 2 - 3 n - 2 n = 0
⇔
n
2
-
5
n
=
0
⇔
n
(
n
-
5
)
=
0
⇔ 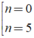
So sánh điều kiện ta có n = 5 thỏa mãn.
Chọn A
Một đa giác có số đường chéo bằng số cạnh của đa giác thì đa giác có số cạnh là?
A. 5.
B. 6.
C. 4.
D. 7.
Đa giác nào có số đường chéo.
a, Bằng số cạnh
b,Gấp đôi số cạnh
Số đường chéo của một đa giác \(n\) cạnh \(\left(n>3\right)\)được tính bởi công thức \(\frac{n\left(n-3\right)}{2}\)
a) Số đường chéo bằng số cạnh có nghĩa là \(\frac{n\left(n-3\right)}{2}=n\Leftrightarrow n^2-3n=2n\Leftrightarrow n^2-5n=0\Leftrightarrow n\left(n-5\right)=0\Leftrightarrow\orbr{\begin{cases}n=0\left(loại\right)\\n=5\left(nhận\right)\end{cases}}\)
Vậy hình ngũ giác có số đường chéo bằng số cạnh.
Số đường chéo gấp đôi số cạnh có nghĩa là \(\frac{n\left(n-3\right)}{2}=2n\Leftrightarrow n^2-3n=4n\Leftrightarrow n^2-7n=0\Leftrightarrow n\left(n-7\right)=0\Leftrightarrow\orbr{\begin{cases}n=0\left(loại\right)\\n=7\left(nhận\right)\end{cases}}\)
Vậy hình thất giác có số đường chéo gấp đôi số cạnh.
Các bạn ơi giúp mik với
Cho đa giác đều n cạnh ( n ≥ 4 ) . Tìm n để đa giác có số đường chéo bằng số cạnh?
A. n = 5
B. n = 16
C. n = 6
D. n = 8
Đáp án A
Phương pháp
Tìm số cạnh và số đường chéo của đa giác đều n cạnh.
Cách giải
Khi nối hai đỉnh bất kì của đa giác ta được một số đoạn thẳng, trong đó bao gồm cạnh của đa giác và đường chéo của đa giác đó.
Đa giác đều n cạnh có n đỉnh, do đó số đường chéo là C n 2 − n
Theo giả thiết bài toán ta có
C n 2 − n = n ⇔ C n 2 = 2 n ⇔ n ! 2 ! n − 2 ! = 2 n ⇔ n n − 1 = 4 n ⇔ n − 1 = 4 ⇔ n = 5
Cho đa giác đều n cạnh (n ≥ 4). Tìm n để đa giác có số đường chéo bằng số cạnh?
A. n = 5
B. n = 16
C. n = 6
D. n = 8
Đáp án A
Phương pháp
Tìm số cạnh và số đường chéo của đa giác đều n cạnh.
Cách giải
Khi nối hai đỉnh bất kì của đa giác ta được một số đoạn thẳng, trong đó bao gồm cạnh của đa giác và đường chéo của đa giác đó.
Đa giác đều n cạnh có n đỉnh, do đó số đường chéo là C n 2 - n
Theo giả thiết bài toán ta có

a) Tính số đường chéo của đa giác có 24 cạnh
b) Tính số cạnh của đa giác biết đường chéo là 170 đường
a) \(\frac{\left(24-3\right).24}{2}=252\)đường chéo
b) \(\left(n-3\right).n=340\)
\(n^2-3n=340\)
\(n^2-3n-340=0\)
\(n^2-20n+17n-340=0\)
\(n\left(n-20\right)+17\left(n-20\right)\)
\(\left(n+17\right)\left(n-20\right)=0\)
\(\Leftrightarrow\)\(\orbr{\begin{cases}n+17=0\\n-20=0\end{cases}}\)\(\Leftrightarrow\)\(\orbr{\begin{cases}n=-17\\n=20\end{cases}}\)
n = -17 ( loại )
n = 20 ( nhận )
Vậy n = 20 hay số cạnh của đa giác là 20
1 Đa giác có n cạnh có :
- Số đường chéo từ 1 đỉnh là : (n - 3)
- Số đỉnh là n
Do 1 đường chéo nối 2 đỉnh
=> 1 Đa giác có n cạnh có n(n - 3)/2 đường chéo
biết tổng số đường chéo là 170
=> n(n - 3)/2 = 170
=> n² - 3n - 340 = 0
∆ = (-3)² - 4.(-340) = 1369
=> √∆ = 37
=> n = ... (tự giải)
b) Đa giác có n cạnh có :
- Số đường chéo từ 1 đỉnh là : (n - 3)
- Số đỉnh là n
Do 1 đường chéo nối 2 đỉnh
=> 1 Đa giác có n cạnh có n \(\frac{\left(n+3\right)}{2}\)đường chéo
Biết tổng số đường chéo là 170
\(\Rightarrow\frac{n\left(n-3\right)}{2}=170\)
\(\Rightarrow n^2-3-340=0\)
\(\Delta=\left(-3\right)^2-4.\left(-340\right)=1369\)
\(\sqrt{\Delta}=37\)
\(\Rightarrow n=37\)
Một đa giác đều có số đường chéo gấp 33 lần số cạnh . số đo mỗi góc của đa giác đều đó bằng bao nhiêu độ ?
Số đường chéo của đa giác đều n cạnh là \(\dfrac{n\left(n-3\right)}{2}\)
Số đường chéo bằng 33 số cạnh
\(\Rightarrow\dfrac{n\left(n-3\right)}{2}=33n\Rightarrow n\left(n-3\right)=66n\\
\Rightarrow n-3=66\\
\Rightarrow n=69\)
Suy ra đa giác đều đó có 69 cạnh
Số đo mỗi góc là \(\dfrac{180\cdot33+360}{69}\approx91,3\)