Hãy viết công thức tính đen ta và hệ thức Vi-ét
HD
Những câu hỏi liên quan
Không giải phương trình, dùng hệ thức Vi-ét, hãy tính tổng và tích các nghiệm của mỗi phương trình 2 x 2 + 9x + 7 = 0
2 x 2 + 9x + 7 = 0
∆ = 9 2 - 4.2.7 = 81 - 56 = 25 > 0
Do đó, phương trình có hai nghiệm phân biệt
Theo hệ thức Vi – et ta có:
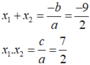
Đúng 0
Bình luận (0)
Không giải phương trình, dùng hệ thức Vi-ét, hãy tính tổng và tích các nghiệm của mỗi phương trình 5 x 2 + x + 2 = 0
Ta có: ∆ = 1 2 -4.5.2 = 1 - 40 = -39 < 0
Đúng 0
Bình luận (0)
Không giải phương trình, dùng hệ thức Vi-ét, hãy tính tổng và tích các nghiệm của mỗi phương trình 2 x 2 – 7x +2 =0
Ta có: ∆ = - 7 2 -4.2.2 =49 -16 =33 >0
Phương trình có 2 nghiệm phân biệt .Theo hệ thức Vi-ét, ta có:
x 1 + x 2 =-b/a =7/2 ; x 1 x 2 =c/a =2/2 =1
Đúng 0
Bình luận (0)
Không giải phương trình, dùng hệ thức Vi-ét, hãy tính tổng và tích các nghiệm của mỗi phương trình 1,4 x 2 -3x +1,2 =0
Ta có : ∆ = - 3 2 -4.1,4.1,2 =9 – 6,72 =2,28 >0
Phương trình có 2 nghiệm phân biệt .Theo hệ thức Vi-ét, ta có:
x 1 + x 2 = -b/a = 3/(1,4) = 30/14 = 15/7 ; x 1 x 2 = c/a = (1,2)/(1,4) = 12/14 = 6/7
Ta có: Δ = 1 2 -4.5.2 = 1 - 40 = -39 < 0
Đúng 0
Bình luận (0)
Không giải phương trình, dùng hệ thức Vi-ét, hãy tính tổng và tích các nghiệm của mỗi phương trình (2 - 3 ) x 2 + 4x + 2 + 2 = 0
Ta có: ∆ ’ = 2 2 – (2 - 3 )(2 + 2 ) =4 -4 - 2 2 +2 3 + 6
= 2 3 - 2 2 + 6 >0
Phương trình 2 nghiệm phân biệt .Theo hệ thức Vi-ét, ta có:
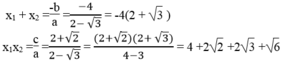
Đúng 0
Bình luận (0)
Hãy nêu cách chứng minh hệ thức Vi-ét ?
HELP ME PLEZ !
Quá dễ :
Xét 2 trường hợp:
\(\text{*Trường hợp 1 :}\Delta=0\)
Dùng công thức nghiệm rồi tìm tổng và tích các nghiệm là ra ( lưu ý là denta =0 nên có thể dùng bfa'p thế )
\(\text{*Trường hợp 2}:\Delta\ge0\)
tương tự t/h 1
Kết luận ....
Đúng 0
Bình luận (0)
pt bậc 2 và hệ thức vi-ét nha
a: Thay m=1 vào phương trình, ta được:
\(x^2-\left(2\cdot1-1\right)x+2\cdot1-4=0\)
=>\(x^2-x-2=0\)
=>(x-2)(x+1)=0
=>\(\left[{}\begin{matrix}x-2=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
b: \(\text{Δ}=\left[-\left(2m-1\right)\right]^2-4\cdot1\cdot\left(2m-4\right)\)
\(=\left(2m-1\right)^2-4\left(2m-4\right)\)
\(=4m^2-4m+1-8m+16\)
\(=4m^2-12m+17=4m^2-12m+9+8\)
\(=\left(2m-3\right)^2+8>=8>0\forall m\)
=>Phương trình luôn có hai nghiệm phân biệt
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=\dfrac{-\left[-\left(2m-1\right)\right]}{1}=2m-1\\x_1\cdot x_2=\dfrac{c}{a}=\dfrac{2m-4}{1}=2m-4\end{matrix}\right.\)
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}x_1+x_2=2m-1\\x_1-2x_2=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x_2=2m-1-3=2m-4\\x_1+x_2=2m-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x_2=\dfrac{2}{3}m-\dfrac{4}{3}\\x_1=2m-1-\dfrac{2}{3}m+\dfrac{4}{3}=\dfrac{4}{3}m+\dfrac{1}{3}\end{matrix}\right.\)
\(x_1\cdot x_2=2m-4\)
=>\(\left(\dfrac{2}{3}m-\dfrac{4}{3}\right)\left(\dfrac{4}{3}m+\dfrac{1}{3}\right)=2m-4\)
=>\(\dfrac{1}{9}\left(2m-4\right)\left(4m+1\right)=2m-4\)
=>\(\left(2m-4\right)\left(4m+1\right)=18m-36\)
=>\(\left(m-2\right)\left(8m+2\right)-18\left(m-2\right)=0\)
=>\(\left(m-2\right)\left(8m+2-18\right)=0\)
=>\(\left(m-2\right)\left(8m-16\right)=0\)
=>\(8\left(m-2\right)^2=0\)
=>\(\left(m-2\right)^2=0\)
=>m-2=0
=>m=2(nhận)
c:
\(x_1^2\cdot x_2+x_1\cdot x_2^2+3\left(x_1+x_2\right)=0\)
=>\(x_1x_2\left(x_1+x_2\right)+3\left(x_1+x_2\right)=0\)
=>\(\left(x_1+x_2\right)\left(x_1x_2+3\right)=0\)
=>\(\left(2m-1\right)\left(2m-4+3\right)=0\)
=>\(\left(2m-1\right)^2=0\)
=>2m-1=0
=>2m=1
=>\(m=\dfrac{1}{2}\)
d: \(A=x_1^2+x_2^2\)
\(=\left(x_1+x_2\right)^2-2x_1x_2\)
\(=\left(2m-1\right)^2-2\left(2m-4\right)\)
\(=4m^2-4m+1-4m+8\)
\(=4m^2-8m+9\)
\(=4m^2-8m+4+5=\left(2m-2\right)^2+5>=5\forall m\)
Dấu '=' xảy ra khi 2m-2=0
=>2m=2
=>m=1
e: \(\left\{{}\begin{matrix}x_1+x_2=2m-1\\x_1\cdot x_2=2m-4\end{matrix}\right.\)
=>\(x_1+x_2-x_1x_2=2m-1-\left(2m-4\right)=2m-1-2m+4=3\)
f: \(\dfrac{1}{x_1}+\dfrac{1}{x_2}>=1\)
=>\(\dfrac{x_1+x_2}{x_1x_2}>=1\)
=>\(\dfrac{2m-1}{2m-4}-1>=0\)
=>\(\dfrac{2m-1-2m+4}{2m-4}>=0\)
=>\(\dfrac{3}{2m-4}>=0\)
=>2m-4>0
=>2m>4
=>m>2
Đúng 2
Bình luận (0)
Cho phương trình:-2x2 +3x+6=0
Không giải phương trình, hãy tính giá trị biểu thức |x1-x2| biết x1, x2 là nghiệm của PT trên.
*Giải bằng Hệ thức Vi-ét!
Vì P = 6 / -2 = -3 < 0
=> Phương trình có hai nghiệm trái dấu
Áp dụng định lí Viet ta có:
\(\hept{\begin{cases}x_1x_2=\frac{6}{-2}\\x_1+x_2=\frac{3}{2}\end{cases}}\)
Ta có: \(\left|x_1-x_2\right|^2=\left(x_1+x_2\right)^2-4x_1x_2=\left(\frac{3}{2}\right)^2-4\left(\frac{6}{-2}\right)=\frac{57}{4}\)
=> \(\left|x_1-x_2\right|=\frac{\sqrt{57}}{2}\)
Cho phương trình 7x2 + 2(m – 1)x - m2 = 0
Trong trường hợp phương trình có nghiệm, dùng hệ thức Vi-ét, hãy tính tổng các bình phương hai nghiệm của phương trình theo m.
Gọi hai nghiệm của phương trình là x1; x2.
Theo định lý Vi-et ta có: 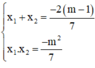
Khi đó:
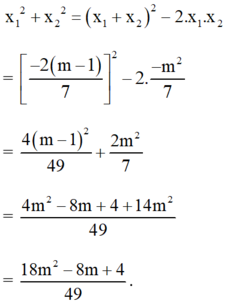
Đúng 0
Bình luận (0)



