Hãy so sánh số trung bình, phương sai và độ lệch chuẩn của ba mẫu só liệu sau:
Mẫu 1: 0,1; 0,3; 0,5; 0,5; 0,3; 0,7.
Mẫu 2: 1,1; 1, 3; 1,5; 1,5; 1,3; 1,7.
Mẫu 3: 1; 3; 5; 5; 3; 7.
Em hãy tìm hiểu chiều cao của tất cả các bạn trong tổ và lập mẫu số liệu với kết quả tăng dần. Với mẫu số liệu đó, hãy tìm:
a) Số trung bình cộng, trung vị và tứ phân vị;
b) Khoảng biến thiên và khoảng tứ phân vị;
c) Phương sai và độ lệch chuẩn.
Ví dụ, ta có bảng đo chiều cao của các bạn trong tổ như sau:
160 | 162 | 164 | 165 | 172 | 174 | 177 | 178 | 180 |
a) Sắp xếp mẫu số liệu theo thứ tự không giảm ta được:
160 162 164 165 172 174 177 178 180
Số trung bình cộng của mẫu số liệu trên là:
\(\overline x = \frac{{160\;\; + 162\;\; + 164\;\;\; + \;\;165\;\; + \;172\;\; + \;174\;\; + \;177\; + \;\;178\; + \;180}}{9} = \frac{{1532}}{9}\)
Trung vị của mẫu số liệu trên là: Do mẫu số liệu trên có 9 số liệu ( lẻ ) nên trung vị \({Q_2} = 172\)
Tứ phân vị của mẫu số liệu trên là:
- Trung vị của dãy 160 162 164 165 là: \({Q_1} = 163\)
- Trung vị của dãy 174 177 178 180 là: \({Q_3} = 177,5\)
- Vậy tứ phân vị của mẫu số liệu là: \({Q_1} = 163\), \({Q_2} = 172\), \({Q_3} = 177,5\)
b) Khoảng biến thiên của mẫu số liệu trên là: \(R = {x_{\max }} - {x_{\min }} = 180 - 160 = 20\)
Khoảng tứ phân vị của mẫu số liệu trên là: \({\Delta _Q} = {Q_3} - {Q_1} = 177,5 - 163 = 14,5\)
c) Phương sai của mẫu số liệu trên là:
\({s^2} = \frac{{\left[ {{{\left( {160 - \overline x } \right)}^2} + {{\left( {162 - \overline x } \right)}^2} + ... + {{\left( {180 - \overline x } \right)}^2}} \right]}}{9} \approx 50,84\)
Độ lệch chuẩn của mẫu số liệu trên là: \(s = \sqrt {{s^2}} \approx 7,13\)
Bài 1: cho mẫu số liệu sau: 200 210 225 225 280 a) tìm số trung bình, trung vị , mốt b) tìm khoảng thiên nhiên, khoảng tứ phân vị c) tìm phương sai và độ lệch chuẩn
Giúp mình bài tập với ạ
Câu 1 Chiều cao của một tổ tiếp viên hàng không được ghi lại lần lượt là
160 170 165 167 172 166 168
a.Tìm giá trị trung bình
b.Tìm tứ phân vị của mẫu số liệu
c.Tìm độ lệch chuẩn và phương sai của mẫu số liệu
Câu 2 Cho hình bình hành ABCD
a.Tính Vectơ AB+Vectơ CD+Vectơ BC+Vectơ DA=?
b.Với điểm M bất kì chứng minh rằng Vectơ MA+Vectơ MC=Vectơ MD+Vectơ MB
Câu 3 cho parabol(P):y=ax2+bx+c,(a≠ 0) đi qua điểm A(2;3) và có đỉnh I(1;2) xác định P
Câu 3:
Theo đề, ta có;
\(\left\{{}\begin{matrix}4a+2b+c=3\\-\dfrac{b}{2a}=1\\-\dfrac{b^2-4ac}{4a}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-2a\\b^2-4ac=-8a\\4a+2b+c=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=-2a\\4a^2-4ac=-8a\\4a+2b+c=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-2a\\4a\left(a-c\right)=4a\cdot\left(-2\right)\\4a+2b+c=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=-2a\\c=a+2\\4a-4a+a+2=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=-2\\c=3\end{matrix}\right.\)
Câu 3:
Theo đề, ta có;
\(\left\{{}\begin{matrix}4a+2b+c=3\\-\dfrac{b}{2a}=1\\-\dfrac{b^2-4ac}{4a}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-2a\\b^2-4ac=-8a\\4a+2b+c=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=-2a\\4a^2-4ac=-8a\\4a+2b+c=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-2a\\4a\left(a-c\right)=4a\cdot\left(-2\right)\\4a+2b+c=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=-2a\\c=a+2\\4a-4a+a+2=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=-2\\c=3\end{matrix}\right.\)
Cho bảng số liệu.
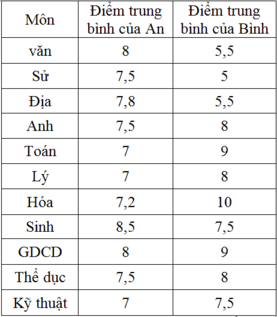
Tính phương sai và độ lệch chuẩn của Bình là:
A. 1,96 và 1,39
B. 1,92 và 1,38
C. 1,3 và 1,69
D. 1,38 và 1,13
Chọn B.
Phương sai và độ lệch chuẩn của Bình là:
Ta có 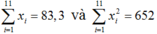
nên 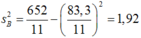
![]()
(36) điểm toán của 1 nhóm gồm 10 học sinh như sau
3 4 4,5 5 6 6,5 8 8,5 9 10
tìm phương sai, độ lệch chuẩn, trung vị và số kiệu bất thường của mẫu số liệu trên
giúp mk vs ạ mk cần gấp
Cho các số liệu thống kê ghi ở bảng sau
Số người xem trong 60 buổi chiếu phim của một rạp chiếu phim nhỏ
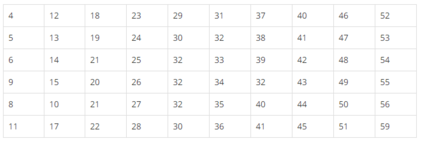
Tính số trung bình, phương sai và độ lệch chuẩn của các số liệu thống kê đã cho
x ≈ 32 n g ư ờ i , s 2 ≈ 219 , 5 ; s ≈ 15 n g ư ờ i
Trong hai mẫu số liệu, mẫu nào có phương sai lớn hơn thì có độ lệch chuẩn lớn hơn, đúng hay sai?
A. Đúng.
B. Sai.
Độ lệch chuẩn bằng căn bậc hai của phương sai.
=> Mẫu nào có phương sai lớn hơn thì có độ lệch chuẩn lớn hơn.
Chọn A.
Mỗi khẳng định sau đúng hay sai?
(1) Nếu các giá trị của mẫu số liệu càng tập trung quanh giá trị trung bình thì độ lệch chuẩn càng lớn.
(2) Khoảng biến thiên chỉ sử dụng thông tin của giá trị lớn nhất và bé nhất, bỏ qua thông tin của các giá trị còn lại.
(3) Khoảng tứ phân vị có sử dụng thông tin của giá trị lớn nhất, giá trị bé nhất.
(4) Khoảng tứ phân vị chính là khoảng biến thiên của nửa dưới mẫu số liệu đã sắp xếp.
(5) Các số đo độ phân tán đều không âm.
Khẳng định (1): Nếu các giá trị của mẫu số liệu càng tập trung quanh giá trị trung bình thì độ lệch của mỗi giá trị so với giá trị trung bình càng nhỏ (tức là \({x_i} - \overline x \) càng nhỏ, với \(i = 1;2;...;n\)), dẫn đến độ lệch chuẩn càng nhỏ.
\(\Rightarrow\)(1) Sai
Khẳng định (2): Khoảng biến thiên R bằng hiệu số giữa giá trị lớn nhất và giá trị nhỏ nhất nên chỉ sử dụng thông tin của giá trị lớn nhất và bé nhất
\(\Rightarrow\) (2) Đúng.
Khẳng định (3): Khoảng tứ phân vị \({\Delta _Q} = {Q_3} - {Q_1}\), các giá trị \({Q_1},{Q_3}\) không bị ảnh hưởng bởi giá trị của giá trị lớn nhất và giá trị nhỏ nhất (với n>4)
\(\Rightarrow\) Sai
Khẳng định (4): Khoảng tứ phân vị chính là khoảng biến thiên của 50% số liệu chính giữa của mẫu số liệu đã sắp xếp
\(\Rightarrow\) Sai.
Khẳng định (5): Các số đo độ phân tán là
Khoảng biến thiên R=Số lớn nhất – Số nhỏ nhất > 0
Trước khi tính khoảng tứ phân vị thì mẫu số liệu được sắp xếp theo thứ tự không giảm
\(\Rightarrow\) \({Q_3} > {Q_1}\) => \({\Delta _Q} = {Q_3} - {Q_1} > 0\)
Phương sai \({s^2} = \frac{{{{\left( {{x_1} - \overline x} \right)}^2} + {{\left( {{x_2} - \overline x} \right)}^2} + ... + {{\left( {{x_n} - \overline x} \right)}^2}}}{n} > 0\)
Độ lệch chuẩn: \(s = \sqrt {{s^2}} > 0\)
\(\Rightarrow\) Các số đo độ phân tán đều không âm
\(\Rightarrow\) (5) Đúng.
Bạn Châu cân lần lượt 50 quả vải thiều Thanh Hà được lựa chọn ngẫu nhiên từ vườn nhà mình và được kết quả như sau:
Cân nặng (đơn vị: gam) | Số quả |
8 | 1 |
19 | 10 |
20 | 19 |
21 | 17 |
22 | 3 |
a) Hãy tìm số trung bình, trung vị, mốt của mẫu số liệu trên
b) Hãy tìm độ lệch chuẩn, khoảng biến thiên, khoảng tứ phân vị và giá trị ngoại lệ của mẫu số liệu trên.
a)
Số trung bình \(\overline x = \frac{{8.1 + 19.10 + 20.19 + 21.17 + 22.3}}{{1 + 10 + 19 + 17 + 3}} = 20,02\)
+) Sắp xếp các giá trị theo thứ tự không giảm: \(8,\underbrace {19,...,19}_{10},\underbrace {20,...,20}_{19},\underbrace {21,...,21}_{17},22,22,22\)
Trung vị \({M_e} = \frac{1}{2}(20 + 20) = 20\)
+) Mốt \({M_o} = 20\)
b)
+) Tình độ lệch chuẩn:
Phương sai \({S^2} = \frac{1}{{50}}\left( {{8^2} + {{10.19}^2} + {{19.20}^2} + {{17.21}^2} + {{3.22}^2}} \right) - 20,{02^2} \approx 3,66\)
=> Độ lệch chuẩn \(S = \sqrt {{S^2}} \approx 1,91\)
+) Khoảng biến thiên \(R = 22 - 8 = 14\)
+) Tứ phân vị: \({Q_1},{Q_2},{Q_3}\)
\({Q_2} = {M_e} = 20\)
\({Q_1}\) là trung vị của mẫu: \(8,\underbrace {19,...,19}_{10},\underbrace {20,...,20}_{14}\). Do đó \({Q_1} = 20\)
\({Q_3}\) là trung vị của mẫu: \(\underbrace {20,...,20}_5,\underbrace {21,...,21}_{17},22,22,22\). Do đó \({Q_3} = 21\)
+) x là giá trị ngoại lệ nếu \(x > 21 + 1,5(21 - 20) = 22,5\) hoặc \(x < 20 - 1,5.(21 - 10) = 18,5\).
Vậy có một giá trị ngoại lệ là 8.