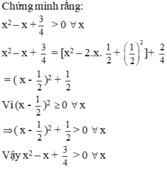\(a,=\left(x^2+3x+\dfrac{9}{4}\right)+\dfrac{19}{4}=\left(x+\dfrac{3}{2}\right)^2+\dfrac{19}{4}\ge\dfrac{19}{4}>0\\ b,=-\left(x^2-5x+\dfrac{25}{4}\right)-\dfrac{7}{4}=-\left(x-\dfrac{5}{2}\right)^2-\dfrac{7}{4}\le-\dfrac{7}{4}< 0\)

a,=(x2+3x+94)+194=(x+32)2+194≥194>0b,=−(x2−5x+254)−74=−(x−52)2−74≤−74<0

E=4x^​2​+5x+5>0 với mọi x

=(4x^​2 +4x+1)+4

=(2x+1)\(^2\)+4

Với mọi x thuộc R thì (2x+1)\(^2\)>=0

Suy ra(2x+1)\(^2\)+4>=4>0

Hay E>0 với mọi x thuộc R(đpcm)

F=5x²​-6x+7>0 với mọi x

=(5x\(^2\)-6x+\(\dfrac{36}{25}\))+\(\dfrac{139}{25}\)

=5\(\left(x-\dfrac{6}{5}\right)^2\)+\(\dfrac{139}{25}\)

Với mọi x thuộc R thì 5\(\left(x-\dfrac{6}{5}\right)^2\)>=0

Suy ra 5\(\left(x-\dfrac{6}{5}\right)^2\)+\(\dfrac{139}{25}\)>0

Hay F >0 với mọi x(đpcm)

G=-x^​2​​+5x -6<0 với mọi x​

=-(x^​2​​-5x+6,25)+0,25

=-(x-2,5)² +0,25

Với mọi x thuộc R thì -(x-2,5)² <=0

Suy ra -(x-2,5)² +0,25<0

Hay G<0 với mọi x (đpcm)

chúc bạn học tốt ạ

2. -x² + x - 33 = -x² + x - 1/4 - 131/4 = -( x² - x + 1/4 ) - 131/4 = -( x - 1/2 )² - 131/4

-( x - 1/2 )² ≤ 0 ∀ x => -( x - 1/2 )² - 131/4 ≤ -131/4 < 0 ∀ x ( đpcm )

3. x² + 4x + 33 = x² + 4x + 4 + 29 = ( x + 2 )² + 29

( x + 2 )² ≥ 0 ∀ x => ( x + 2 )² + 29 ≥ 29 > 0 ∀ x ( đpcm )

4. x² + 8x = x² + 8x + 16 - 16 = ( x + 4 )² - 16

( x + 4 )²  ≥ 0 ∀ x =>  ( x + 4 )² - 16 ≥ -16 ∀ x

Đẳng thức xảy ra <=> x + 4 = 0 => x = -4

Vậy GTNN của biểu thức = -16, đạt được khi x = -4 

Ta có:

\(x^2-x+1\)

\(=x^2-2\cdot\dfrac{1}{2}\cdot x+\dfrac{1}{4}+\dfrac{3}{4}\)

\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\)

Mà: \(\left(x-\dfrac{1}{2}\right)^2\ge0\forall x\) và \(\dfrac{3}{4}>0\)

Nên: \(x^2-x+1>0\)

\(x^2-x+1\)

\(=x^2-\dfrac{1}{2}.x-\dfrac{1}{2}.x+\dfrac{1}{4}+\dfrac{3}{4}\)

\(=x\left(x-\dfrac{1}{2}\right)-\dfrac{1}{2}\left(x-\dfrac{1}{2}\right)+\dfrac{3}{4}\)

\(=\left(x-\dfrac{1}{2}\right)\left(x-\dfrac{1}{2}\right)+\dfrac{3}{4}\)

\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\) với mọi x ( đpcm )

\(x^2-x+1=x^2-2.x.\dfrac{1}{2}+\left(\dfrac{1}{2}\right)^2+\dfrac{3}{4}=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\\ Mà:\left(x-\dfrac{1}{2}\right)^2>0\forall x\in R\\ Vậy:\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x\in R\\ Vậy:x^2-x+1>0\forall x\in R\)

\(-x^2+8x-19=-\left(x^2-8x+16\right)-3=-\left(x-4\right)^2-3\le-3< 0\)

a) \(x^2+xy+y^2+1\)

\(=x^2+xy+\dfrac{y^2}{4}-\dfrac{y^2}{4}+y^2+1\)

\(=\left(x+\dfrac{y}{2}\right)^2+\dfrac{3y^2}{4}+1\)

mà \(\left\{{}\begin{matrix}\left(x+\dfrac{y}{2}\right)^2\ge0,\forall x;y\\\dfrac{3y^2}{4}\ge0,\forall x;y\end{matrix}\right.\)

\(\Rightarrow\left(x+\dfrac{y}{2}\right)^2+\dfrac{3y^2}{4}+1>0,\forall x;y\)

\(\Rightarrow dpcm\)

b) \(...=x^2-2x+1+4\left(y^2+2y+1\right)+z^2-6z+9+1\)

\(=\left(x-1\right)^2+4\left(y^{ }+1\right)^2+\left(z-3\right)^2+1>0,\forall x.y\)

\(\Rightarrow dpcm\)

b.

$x^2+4y^2+z^2-2x-6z+8y+15=(x^2-2x+1)+(4y^2+8y+4)+(z^2-6z+9)+1$

$=(x-1)^2+(2y+2)^2+(z-3)^2+1\geq 0+0+0+1>0$ với mọi $x,y,z$

Ta có đpcm.

x²-2.\(\frac{5}{2}\)x + \(\frac{25}{4}\)-\(\frac{25}{4}\)+7= (x-\(\frac{5}{2}\))² +\(\frac{3}{4}\)\(\ge\)\(\frac{3}{4}\)>0  với mọi x