Từ đồ thị của hàm số \(y = \tan x\), hãy tìm các giá trị x sao cho \(\tan x = 0.\)
QL
Những câu hỏi liên quan
Quan sát đồ thị hàm số y tan x ở Hình 30a) Nêu tập giá trị của hàm số y tan xb) Gốc tọa độ có là tâm đối xứng của đồ thị hàm số hay không? Từ đó kết luận tính chẵn, lẻ của hàm số y tan xc) Bằng cách dịch chuyển đồ thị hàm số y tan x trên khoảng left( { - frac{pi }{2};frac{pi }{2}} right) song song với trục hoành sang phải theo đoạn có độ dài π, ta nhận được đồ thị hàm số y tan x trên khoảng left( {frac{pi }{2};frac{{3pi }}{2}} right) hay không? Hàm số y tan x có tuần hoàn hay k...
Đọc tiếp
Quan sát đồ thị hàm số \(y = \tan x\) ở Hình 30
a) Nêu tập giá trị của hàm số \(y = \tan x\)
b) Gốc tọa độ có là tâm đối xứng của đồ thị hàm số hay không? Từ đó kết luận tính chẵn, lẻ của hàm số \(y = \tan x\)
c) Bằng cách dịch chuyển đồ thị hàm số \(y = \tan x\) trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) song song với trục hoành sang phải theo đoạn có độ dài π, ta nhận được đồ thị hàm số \(y = \tan x\) trên khoảng \(\left( {\frac{\pi }{2};\frac{{3\pi }}{2}} \right)\) hay không? Hàm số \(y = \tan x\) có tuần hoàn hay không?
d) Tìm khoảng đồng biến, nghịch biến của hàm số \(y = \tan x\)
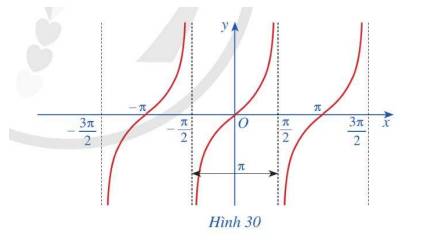
a) Tập giá trị của hàm số \(y = \tan x\) là R
b) Gốc tọa độ là tâm đối xứng của đồ thị hàm số
Như vậy, hàm số \(y = \tan x\)là hàm số lẻ
c) Bằng cách dịch chuyển đồ thị hàm số \(y = \tan x\) trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) song song với trục hoành sang phải theo đoạn có độ dài π, ta nhận được đồ thị hàm số \(y = \tan x\) trên khoảng \(\left( {\frac{\pi }{2};\frac{{3\pi }}{2}} \right)\)
Như vậy, hàm số \(y = \tan x\) có tuần hoàn
d) Hàm số \(y = \tan x\)đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k\pi ;\frac{\pi }{2} + k\pi } \right)\) với \(k \in Z\)
Đúng 0
Bình luận (0)
Sử dụng đồ thị đã vẽ ở Hình 1.16, hãy xác định các giá trị của x trên đoạn \(\left[ { - \pi ;\frac{{3\pi }}{2}} \right]\) để hàm số \(y = \tan x\) nhận giá trị âm.
Hàm số nhận giá trị âm ứng với phần đồ thị nằm dưới trục hoành. Từ đồ thị ta suy ra trên đoạn \(\left[ { - \pi ;\frac{{3\pi }}{2}} \right]\), thì \(y < 0\) khi \(x\; \in \left( { - \frac{\pi }{2};0} \right) \cup \left( {\frac{\pi }{2};\;\pi } \right)\)
Đúng 0
Bình luận (0)
Bài 1. Cho hàm số y 2x-1a) Tính giá trị của hàm số y khi x0; x1; x -2b) Tìm giá trị của x khi y3Bài 2. Cho hàm số y -3xa) Vẽ đồ thị hàm sốb) Tìm trên đồ thị hàm số điểm có hoành độ bằng 2c) Tìm trên đồ thị hàm số điểm có tung độ bằng -6
Đọc tiếp
Bài 1. Cho hàm số
y= 2x-1
a) Tính giá trị của hàm số y khi x=0; x=1; x= -2
b) Tìm giá trị của x khi y=3
Bài 2. Cho hàm số
y= -3x
a) Vẽ đồ thị hàm số
b) Tìm trên đồ thị hàm số điểm có hoành độ bằng 2
c) Tìm trên đồ thị hàm số điểm có tung độ bằng -6
Bài 1:
a: x=0 => y=-1
x=1 =>y=1
Đúng 1
Bình luận (0)
cho hàm số \(y=x^2-2x+3\) có đồ thị (P). lập bảng biến thiên và vẽ đồ thị (P). từ đó tìm các giá trị của tham số m sao cho phương trình \(x^2-2x+3-m=0\) có 2 nghiệm phân biệt
Vẽ đồ thị hàm số y=f(x)=-0,5x. Bằng đồ thị hãy tìm:
a) f(2);f(-1);f(-4);f(0)
b) Các giá trị của x khi y=-1; y=0; y=2,5
c) Các giá trị của x khi y âm, y dương
a) f(2) = 0,5 . 2 = 1
f(-2) = 0,5 . (-2) = -1
f(4) = 0,5 . 4 = 2
f(0) = 0,5 . 0 = 0
b) Ta có : y = 0,5x
Với y = -1 => -1 = 0,5x => x = -1 : 0,5 = -2
Với y = 0 => 0 = 0,5x => x = 0 : 0,5 = 0
Với y = 2,5 => 2,5 = 0,5x => x = 2,5 : 0,5 = 5
c) * y nhận giá trị dương khi y > 0
=> 0,5x > 0
=> x > 0
Vậy y nhận giá trị dương khi x nhận giá trị dương
* y nhận giá trị âm khi y < 0
=> 0,5x < 0
=> x < 0
Vậy y nhận giá trị âm khi x nhận giá trị âm
Học tốt
a) Thay f(2);f(-1);f(-4);f(0) vào đồ thị hàm số y=f(x)=-0,5x
f(2) = 0,5 . 2 = 1
f(-2) = 0,5 . (-2) = -1
f(4) = 0,5 . 4 = 2
f(0) = 0,5 . 0 = 0
b) Ta có : y = 0,5x
+) y = -1 => -1 = 0,5x => x = -1 : 0,5 = -2
+) y = 0 => 0 = 0,5x => x = 0 : 0,5 = 0
+) y = 2,5 => 2,5 = 0,5x => x = 2,5 : 0,5 = 5
c) *Khi y có giá trị dương thì y > 0
=> 0,5x > 0
=> x > 0
Vậy y có giá trị dương khi x có giá trị dương
*Khi y có giá trị âm thì y < 0
=> 0,5x < 0
=> x < 0
Vậy y có giá trị âm khi x có giá trị âm
Tìm tất cả các giá trị thực của tham số m sao cho hàm số
y
tan
x
-
2
tan
x
-
m
đồng biến trên khoảng
0
;
π
4...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = tan x - 2 tan x - m đồng biến trên khoảng 0 ; π 4 ?
A. 1≤ m < 2.
B. m≤ 0 .
C. m> 2.
D. Cả A và B đúng
+) Điều kiện tanx ≠ m
Điều kiện cần để hàm số đồng biến trên (0; π/4) là m ∉ (0;1)
+) đạo hàm:
y ' = ( tan 2 x + 1 ) ( 2 - m ) ( tan x - m ) 2 = 2 - m cos 2 x . ( tan x - m ) 2
+) Ta thấy:
1 cos 2 x . ( tan x - m ) 2 > 0 ; ∀ m ∉ ( 0 ; 1 )
+) Để hàm số đồng biến trên (0; π/4)
⇔ y ' > 0 m ∉ ( 0 ; 1 ) ⇔ - m + 2 > 0 m ≤ 0 ; m ≥ 1 ⇔ m ≤ 0 h o ặ c 1 ≤ m < 2
Chọn D.
Đúng 0
Bình luận (0)
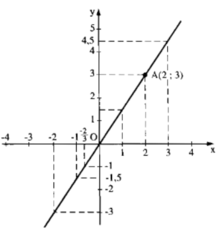
Vẽ đồ thị của hàm số y = f(x) = 1,5x. Bằng đồ thị, hãy tìm: Giá trị của x khi y = -1; y = 0; y = 4,5.
Vẽ đồ thị hàm số:
Vẽ hệ trục tọa độ Oxy
Với x= 2 thì y = 1,5. 2 = 3 ta được điểm A(2; 3)
Vẽ đường thẳng đi qua O, A ta được đồ thị hàm số y = f(x) = 1,5x
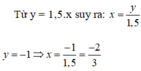
Đúng 0
Bình luận (0)
Vẽ đồ thị hàm số y = f(x) = -0,5x. Bằng đồ thị hãy tìm:
Giá trị của x khi y = -1 ; y = 0 ; y = 2,5
Trên đồ thị ta thấy
y = -1 ⇒ x = 2
y = 0 ⇒ x = 0
y = 2,5 ⇒ x = -5
Đúng 0
Bình luận (0)
Vẽ đồ thị hàm số y = 1,5x. Bằng đồ thị, hãy tìm:
a) Các giá trị f(1); f(-1); f(-2); f(2); f(0).
b) Giá trị của x khi y = -1; y = 0; y = 4,5.
c) Các giá trị của x khi y dương; khi y âm.




