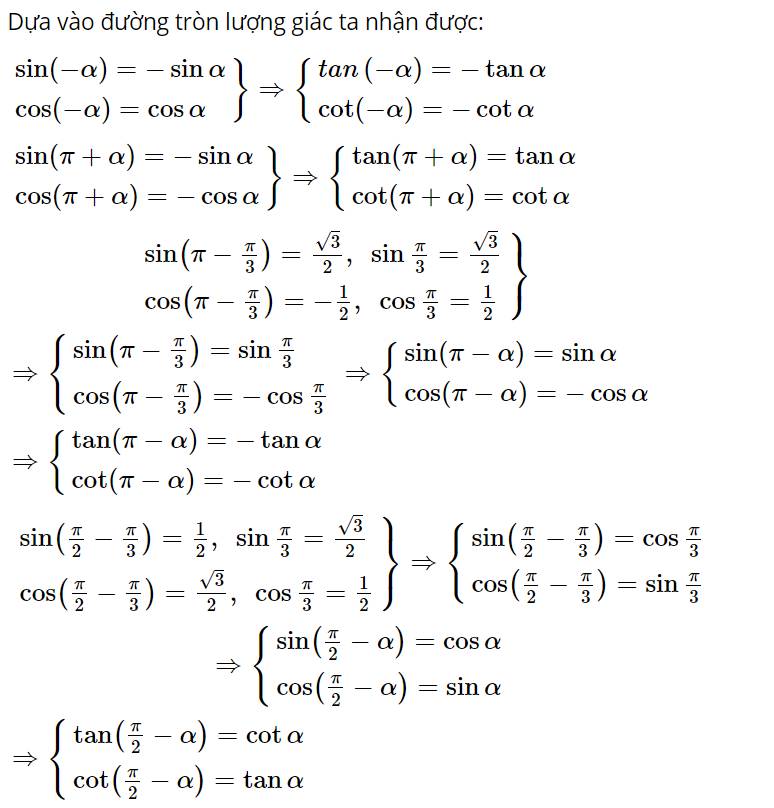Tìm giác trị lượng giác của góc lượng giác \(\beta = - \frac{\pi }{4}\)
QL
Những câu hỏi liên quan
Biểu diễn các góc lượng giác alpha - frac{{5pi }}{6},;beta frac{pi }{3},;gamma frac{{25pi }}{3},delta frac{{17pi }}{3} trên đường tròn lượng giác. Các góc nào có điểm biểu diễn trùng nhau? A. beta và gamma B. alpha, beta, gamma C. beta ,gamma ,delta D. alpha và beta ,
Đọc tiếp
Biểu diễn các góc lượng giác \(\alpha = - \frac{{5\pi }}{6},\;\beta = \frac{\pi }{3},\;\gamma = \frac{{25\pi }}{3},\delta = \frac{{17\pi }}{3}\) trên đường tròn lượng giác. Các góc nào có điểm biểu diễn trùng nhau?
A. \(\beta \) và \( \gamma \)
B. \(\alpha, \beta, \gamma \)
C. \(\beta ,\gamma ,\delta \)
D. \(\alpha \) và \(\beta \),
Ta có: \(\frac{{25\pi }}{3} = \frac{\pi }{3} + 4.2\pi .\) Do đó điểm biểu diễn cung lượng giác \(\frac{{25\pi }}{3}\) trùng với điểm biểu diễn cung lượng giác \(\frac{\pi }{3}\).
Vậy ta chọn đáp án A
Đúng 0
Bình luận (0)
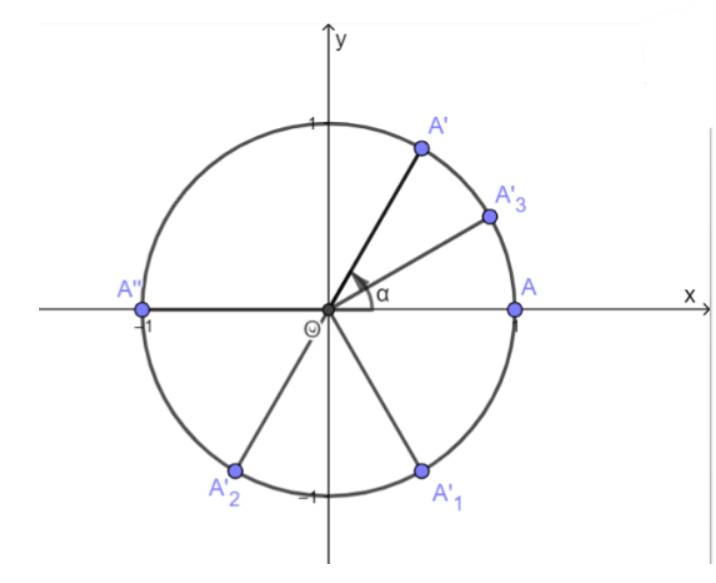
Cho \(\alpha = \frac{\pi }{3}\). Biểu diễn các góc lượng giác \( - \alpha ,\alpha + \pi ,\pi - \alpha ,\frac{\pi }{2} - \alpha \) trên đường tròn lượng giác và rút ra mỗi liên hệ giữ giá trị lượng giác của các góc này với giá trị lượng giác của góc \(\alpha \)
Cho góc lượng giác (Ou,Ov) có số đo là \( - \frac{{11\pi }}{4}\), góc lượng giác (Ou,Ow) có số đó là \(\frac{{3\pi }}{4}\). Tìm số đo của góc lượng giác (Ov,Ow).
Theo hệ thức Chasles, ta có:
\(\begin{array}{l}(Ov,Ow) = (Ou,Ov) - (Ou,Ow) + k2\pi \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \, - \frac{{11\pi }}{4} - \frac{{3\pi }}{4} + k2\pi = - \frac{7}{2} + k2\pi ,\,\,(k \in \mathbb{Z})\end{array}\)
Đúng 0
Bình luận (0)
Biểu diễn các giá trị lượng giác sau qua giá trị lượng giác của góc có số đo từ 0 đến \(\frac{\pi }{4}\) hoặc từ 0 đến \(45^\circ \) và tính
a) \(\cos \frac{{21\pi }}{6}\)
b) \(\sin \frac{{129\pi }}{4}\)
c) \(\tan 1020^\circ \)
\(a,cos\left(\dfrac{21\pi}{6}\right)=cos\left(3\pi+\dfrac{\pi}{2}\right)=cos\left(\pi+\dfrac{\pi}{2}\right)=-cos\left(\dfrac{\pi}{2}\right)=0\\ b,sin\left(\dfrac{129\pi}{4}\right)=sin\left(32\pi+\dfrac{\pi}{4}\right)=sin\left(\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\\ c,tan\left(1020^o\right)=tan\left(5\cdot180^o+120^o\right)=tan\left(120^o\right)=-\sqrt{3}\)
Đúng 1
Bình luận (0)
a) Biểu diễn \(\cos 638^\circ \) qua gí trị lượng giác của góc có số đo từ \(0^\circ \) đến \(45^\circ \)
b) Biểu diễn \(\cot \frac{{19\pi }}{5}\) qua giá trị lượng giác của góc có số đo từ 0 đến \(\frac{\pi }{4}\)
a) \(cos638^o=cos\left(-82^o\right)=cos\left(82^o\right)=sin8^o\)
b) \(cot\dfrac{19\pi}{5}=cot\dfrac{4\pi}{5}=-cot\dfrac{\pi}{5}\)
Đúng 2
Bình luận (0)
Cho góc lượng giác có số đo bằng \(\frac{{5\pi }}{6}\)
a) Xác định điểm M trên đường tròn lượng giác biểu diễn góc lượng giác đã cho.
b) Tính các giá trị lượng giác của góc lượng giác đã cho.
Tham khảo:
a) Ta chia nửa đường tròn thành 6 phần bằng nhau. Khi đó điểm M là điểm biểu diễn bởi góc có số đo \(\frac{{5\pi }}{6}\)
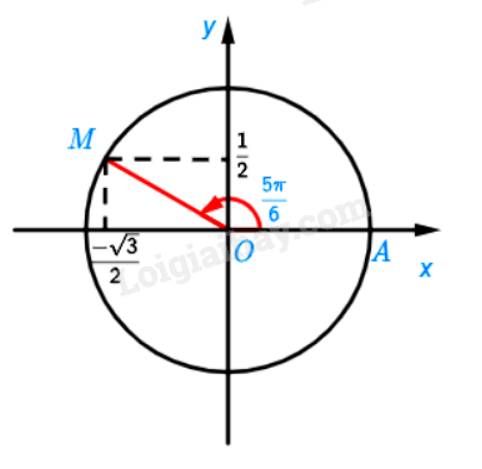
b) Ta có:
\(\sin \left( {\frac{{5\pi }}{6}} \right) = \frac{1}{2};\cos \left( {\frac{{5\pi }}{6}} \right) = \frac{{ - \sqrt 3 }}{2};\tan \left( {\frac{{5\pi }}{6}} \right) = \frac{{ - \sqrt 3 }}{3};\cot \left( {\frac{{5\pi }}{6}} \right) = \frac{{ - 3}}{{\sqrt 3 }}\)
Đúng 0
Bình luận (0)
Xét dấu các giá trị lượng giác của góc lượng giác \(\alpha = \frac{{5\pi }}{6}\)
Do \(\frac{\pi }{2} < \frac{{5\pi }}{6} < \pi \) nên
\(\begin{array}{l}\cos \left( {\frac{{5\pi }}{6}} \right) < 0\\\sin \left( {\frac{{5\pi }}{6}} \right) > 0\\\tan \left( {\frac{{5\pi }}{6}} \right) < 0\\\cot \left( {\frac{{5\pi }}{6}} \right) < 0\end{array}\)
Đúng 0
Bình luận (0)
Tính các giá trị lượng giác của mỗi góc sau: \(225^\circ ; - 225^\circ ; - 1035^\circ \);\(\frac{{5\pi }}{3};\frac{{19\pi }}{2}; - \frac{{159\pi }}{4}\)
\(\begin{array}{l}\cos \left( {{{225}^ \circ }} \right) = \cos \left( {{{180}^ \circ } + {{45}^ \circ }} \right) = - \cos \left( {{{45}^ \circ }} \right) = - \frac{{\sqrt 2 }}{2}\\\sin \left( {{{225}^ \circ }} \right) = \sin \left( {{{180}^ \circ } + {{45}^ \circ }} \right) = - \sin \left( {{{45}^ \circ }} \right) = - \frac{{\sqrt 2 }}{2}\\\tan \left( {225^\circ } \right) = \frac{{\sin \left( {{{225}^ \circ }} \right)}}{{\cos \left( {{{225}^ \circ }} \right)}} = 1\\\cot \left( {225^\circ } \right) = \frac{1}{{\tan \left( {225^\circ } \right)}} = 1\end{array}\)
\(\begin{array}{l}\cos \left( { - {{225}^ \circ }} \right) = \cos \left( {{{225}^ \circ }} \right) = \cos \left( {{{180}^ \circ } + {{45}^ \circ }} \right) = - \cos \left( {{{45}^ \circ }} \right) = - \frac{{\sqrt 2 }}{2}\\\sin \left( { - {{225}^ \circ }} \right) = - \sin \left( {{{225}^ \circ }} \right) = - \sin \left( {{{180}^ \circ } + {{45}^ \circ }} \right) = \sin \left( {{{45}^ \circ }} \right) = \frac{{\sqrt 2 }}{2}\\\tan \left( { - 225^\circ } \right) = \frac{{\sin \left( {{{225}^ \circ }} \right)}}{{\cos \left( {{{225}^ \circ }} \right)}} = - 1\\\cot \left( { - 225^\circ } \right) = \frac{1}{{\tan \left( {225^\circ } \right)}} = - 1\end{array}\)
\(\begin{array}{l}\cos \left( { - {{1035}^ \circ }} \right) = \cos \left( {{{1035}^ \circ }} \right) = \cos \left( {{{6.360}^ \circ } - {{45}^ \circ }} \right) = \cos \left( { - {{45}^ \circ }} \right) = \cos \left( {{{45}^ \circ }} \right) = \frac{{\sqrt 2 }}{2}\\\sin \left( { - {{1035}^ \circ }} \right) = - \sin \left( {{{1035}^ \circ }} \right) = - \sin \left( {{{6.360}^ \circ } - {{45}^ \circ }} \right) = - \sin \left( { - {{45}^ \circ }} \right) = \sin \left( {{{45}^ \circ }} \right) = \frac{{\sqrt 2 }}{2}\\\tan \left( { - 1035^\circ } \right) = \frac{{\sin \left( { - {{1035}^ \circ }} \right)}}{{\cos \left( { - {{1035}^ \circ }} \right)}} = 1\\\cot \left( { - 1035^\circ } \right) = \frac{1}{{\tan \left( { - 1035^\circ } \right)}} = - 1\end{array}\)
\(\begin{array}{l}\cos \left( {\frac{{5\pi }}{3}} \right) = \cos \left( {\pi + \frac{{2\pi }}{3}} \right) = - \cos \left( {\frac{{2\pi }}{3}} \right) = \frac{1}{2}\\\sin \left( {\frac{{5\pi }}{3}} \right) = \sin \left( {\pi + \frac{{2\pi }}{3}} \right) = - \sin \left( {\frac{{2\pi }}{3}} \right) = - \frac{{\sqrt 3 }}{2}\\\tan \left( {\frac{{5\pi }}{3}} \right) = \frac{{\sin \left( {\frac{{5\pi }}{3}} \right)}}{{\cos \left( {\frac{{5\pi }}{3}} \right)}} = - \sqrt 3 \\\cot \left( {\frac{{5\pi }}{3}} \right) = \frac{1}{{\tan \left( {\frac{{5\pi }}{3}} \right)}} = - \frac{{\sqrt 3 }}{3}\end{array}\)
\(\begin{array}{l}\cos \left( {\frac{{19\pi }}{2}} \right) = \cos \left( {8\pi + \frac{{3\pi }}{2}} \right) = \cos \left( {\frac{{3\pi }}{2}} \right) = \cos \left( {\pi + \frac{\pi }{2}} \right) = - \cos \left( {\frac{\pi }{2}} \right) = 0\\\sin \left( {\frac{{19\pi }}{2}} \right) = \sin \left( {8\pi + \frac{{3\pi }}{2}} \right) = \sin \left( {\frac{{3\pi }}{2}} \right) = \sin \left( {\pi + \frac{\pi }{2}} \right) = - \sin \left( {\frac{\pi }{2}} \right) = - 1\\\tan \left( {\frac{{19\pi }}{2}} \right)\\\cot \left( {\frac{{19\pi }}{2}} \right) = \frac{{\cos \left( {\frac{{19\pi }}{2}} \right)}}{{\sin \left( {\frac{{19\pi }}{2}} \right)}} = 0\end{array}\)
\(\begin{array}{l}\cos \left( { - \frac{{159\pi }}{4}} \right) = \cos \left( {\frac{{159\pi }}{4}} \right) = \cos \left( {40.\pi - \frac{\pi }{4}} \right) = \cos \left( { - \frac{\pi }{4}} \right) = \cos \left( {\frac{\pi }{4}} \right) = \frac{{\sqrt 2 }}{2}\\\sin \left( { - \frac{{159\pi }}{4}} \right) = - \sin \left( {\frac{{159\pi }}{4}} \right) = - \sin \left( {40.\pi - \frac{\pi }{4}} \right) = - \sin \left( { - \frac{\pi }{4}} \right) = \sin \left( {\frac{\pi }{4}} \right) = \frac{{\sqrt 2 }}{2}\\\tan \left( { - \frac{{159\pi }}{4}} \right) = \frac{{\cos \left( { - \frac{{159\pi }}{4}} \right)}}{{\sin \left( { - \frac{{159\pi }}{4}} \right)}} = 1\\\cot \left( { - \frac{{159\pi }}{4}} \right) = \frac{1}{{\tan \left( { - \frac{{159\pi }}{4}} \right)}} = 1\end{array}\)
Đúng 0
Bình luận (0)
Góc lượng giác \(\frac{{31\pi }}{7}\) có cùng biểu diễn trên đường tròn lượng giác với góc lượng giác nào sau đây?
\(\frac{{3\pi }}{7};\,\,\frac{{10\pi }}{7};\,\,\frac{{ - 25\pi }}{7}\)
\(\dfrac{31\pi}{7}=\dfrac{3\pi}{7}+2\cdot2\pi\\ -\dfrac{25\pi}{7}=-\dfrac{4\pi}{7}-3\pi\\ \dfrac{10\pi}{7}=\dfrac{3\pi}{7}+\pi\)
\(\Rightarrow\dfrac{31\pi}{7}\) có cùng biểu diễn trên đường tròn lượng giác với góc \(\dfrac{3\pi}{7}\)
Đúng 0
Bình luận (0)