a) \(cos638^o=cos\left(-82^o\right)=cos\left(82^o\right)=sin8^o\)
b) \(cot\dfrac{19\pi}{5}=cot\dfrac{4\pi}{5}=-cot\dfrac{\pi}{5}\)
a) \(cos638^o=cos\left(-82^o\right)=cos\left(82^o\right)=sin8^o\)
b) \(cot\dfrac{19\pi}{5}=cot\dfrac{4\pi}{5}=-cot\dfrac{\pi}{5}\)
Biểu diễn các giá trị lượng giác sau qua giá trị lượng giác của góc có số đo từ 0 đến \(\frac{\pi }{4}\) hoặc từ 0 đến \(45^\circ \) và tính
a) \(\cos \frac{{21\pi }}{6}\)
b) \(\sin \frac{{129\pi }}{4}\)
c) \(\tan 1020^\circ \)
Tính các giá trị lượng giác của góc α, nếu:
a) \(\sin \alpha = \frac{5}{{13}}\) và \(\frac{\pi }{2} < \alpha < \pi \)
b) \(\cos \alpha = \frac{2}{5}\) và \(0 < \alpha < 90^\circ \)
c) \(\tan \alpha = \sqrt 3 \) và \(\pi < \alpha < \frac{{3\pi }}{2}\)
d) \(\cot \alpha = \frac{1}{2}\) và \(270^\circ < \alpha < 360^\circ \)
Cho \(\alpha = \frac{\pi }{3}\). Biểu diễn các góc lượng giác \( - \alpha ,\alpha + \pi ,\pi - \alpha ,\frac{\pi }{2} - \alpha \) trên đường tròn lượng giác và rút ra mỗi liên hệ giữ giá trị lượng giác của các góc này với giá trị lượng giác của góc \(\alpha \)
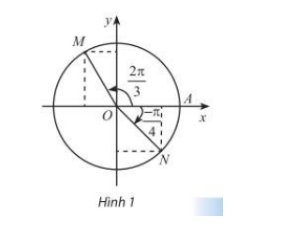
Trong Hình 1, M và N là điểm biểu diễn của các góc lượng giác \(\frac{{2\pi }}{3}\) và \(\frac{\pi }{4}\) trên
đường tròn lượng giác. Xác định tọa độ của M và N trong hệ trục tọa độ Oxy .
Sử dụng máy tính cầm tay để tính
\(\cos 75^\circ \,\,\)và \(\tan \left( { - \frac{{19\pi }}{6}} \right)\)
Tính \(\sin \left( { - \frac{{2\pi }}{3}} \right)\) và \(\tan 495^\circ \)
a) Trong Hình 5, M là điểm biểu diễn của góc lượng giác α trên đường tròn lượng giác. Giải thích vì sao \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\)
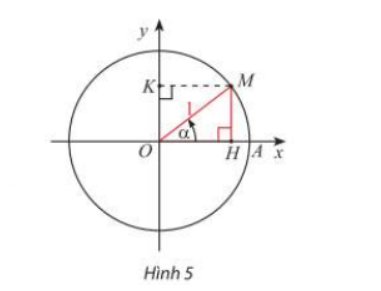
b) Chia cả hai vế của biểu thức ở câu a) cho \({\cos ^2}\alpha \) ta được đẳng thức nào?
c) Chia cả hai vế của biểu thức ở câu a) cho \({\sin ^2}\alpha \) ta được đẳng thức nào?
Rút gọn các biểu thức sau:
a) \(\frac{1}{{\tan \alpha + 1}} + \frac{1}{{\cot \alpha + 1}}\)
b) \(\cos \left( {\frac{\pi }{2} - \alpha } \right) - \sin \left( {\pi + \alpha } \right)\)
c) \(\sin \left( {\alpha - \frac{\pi }{2}} \right) + \cos \left( { - \alpha + 6\pi } \right) - \tan \left( {\alpha + \pi } \right)\cot \left( {3\pi - \alpha } \right)\)
Trong Hình 11, vị trí cabin mà Bình và Cường ngồi trên vòng quay được đánh dấu với điểm B và C.
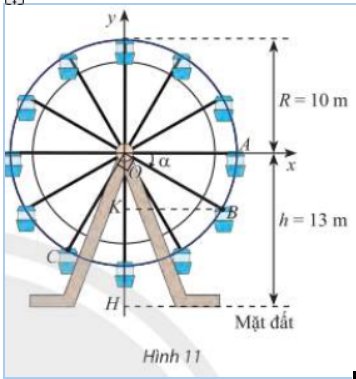
a) Chứng minh rằng chiều cao từ điểm B đến mặt đất bằng \(\left( {13 + 10\sin \alpha } \right)\) mét với α là số đo của một góc lượng giác tia đầu OA, tia cuối OB. Tính độ cao của điểm B so với mặt đất khi \(\alpha = - 30^\circ \)
b) Khi điểm B cách mặt đất 4m thì điểm C cách mặt đất bao nhiêu mét? Làm tròn kết quả đến hàng phần trăm.