Hãy chỉ ra các cặp tam giác vuông bằng nhau dưới đây.
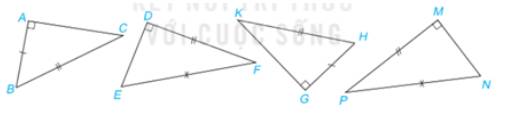
Hãy nêu các trường hợp bằng nhau cho mỗi cặp tam giác trong Hình 17. Từ các điều kiện bằng nhau của hai tam giác, người ta suy ra được các trường hợp bằng nhau sau đây của hai tam giác vuông.
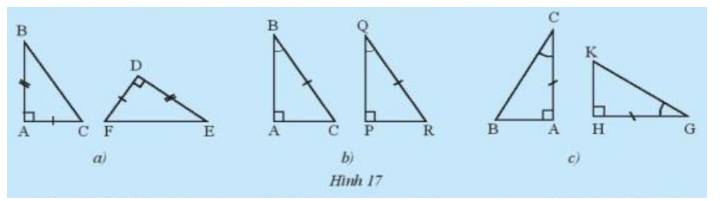
a) Xét \(\Delta{ABC}\) và \(\Delta{DEF}\) có:
AB = DE (gt)
\(\widehat {BAC} = \widehat {EDF}\) (gt)
AC = DF (gt)
\(\Rightarrow \Delta{ABC}=\Delta{DEF}\) (c-g-c)
b) Ta có: \(\widehat B + \widehat C = \widehat Q + \widehat R = 90^0\)
Mà \(\widehat B = \widehat Q\) \( \Rightarrow \widehat C = \widehat R\)
Xét \(\Delta{ABC}\) và \(\Delta{PQR}\) có:
\(\widehat C = \widehat R\) (gt)
BC = QR (gt)
\(\widehat B = \widehat Q\) (gt)
\(\Rightarrow \Delta{ABC}=\Delta{PQR}\) (g-c-g)
c) Xét \(\Delta{ABC}\) và \(\Delta{HKG}\) có:
\(\widehat C = \widehat G\) (gt)
AC = HG (gt)
\(\widehat A = \widehat H\) (gt)
\(\Rightarrow \Delta{ABC}=\Delta{HKG}\) (g-c-g)
Hãy chỉ ra cặp tam giác đồng dạng với nhau từ các tam giác sau đây:
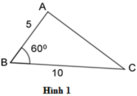
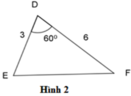
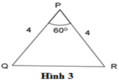
A. Hình 1 và hình 2
B. Hình 2 và hình 3
C. Hình 1 và hình 3
D. Tất cả đều đúng
Có:
B A B C = 5 10 = 1 2 ; D E D F = 3 6 = 1 2 ; P Q P R = 4 4 = 1 ⇒ B A B C = D E D F = 1 2
Xét ΔABC và ΔEDF ta có:
B A B C = D E D F (cmt) ⇔ D E B A = D F B C
B = D = 60 ∘ (gt)
=> ΔABC ~ ΔEDF (c - g - c).
Đáp án: A
Hãy chỉ ra các cặp tam giác đồng dạng với nhau từ các tam giác sau đây (h.38):
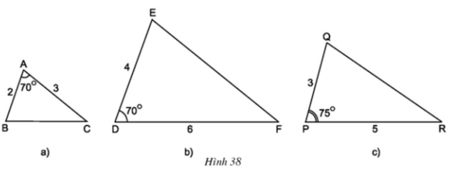
ΔABC và ΔDEF có
∠A = ∠D = 70o
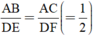
⇒ ΔABC ∼ ΔDEF (c.g.c)
Biết hai tam giác trong Hình 4.11 bằng nhau, em hãy chỉ ra các cặp cạnh tương ứng, các cặp góc tương ứng và viết đúng kí hiệu bằng nhau của cặp tam giác đó.
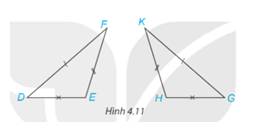
Ta có: Các cặp góc tương ứng là: \(\widehat E = \widehat H;\widehat D = \widehat G;\widehat F = \widehat K\)
Các cặp cạnh tương ứng là:\(ED=HG;EF=HK;DF=GK\)
Các cặp cạnh tương ứng : FE = KH , ED = HG , DF = GK
Các góc tương ứng : góc F = góc K, góc E = góc H, góc D = góc G
Kí hiệu bằng nhau của tam giác đó : ΔDFE=ΔGKH
Quan sát Hình 4. Hai tam giác ABC và MNP có bằng nhau không? Hãy chỉ ra các cặp góc và các cặp cạnh tương ứng bằng nhau.
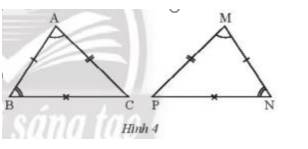
\( \Rightarrow \Delta{ABC}=\Delta{MNP}\) do có các cặp góc và cạnh tương ứng bằng nhau.
Các cặp góc bằng nhau là: \(\widehat A = \widehat M\); \(\widehat B = \widehat N\);\(\widehat C = \widehat P\)
Các cặp cạnh bằng nhau là: \(AB = MN; AC = MP; BC = PN\)
Cho ba điểm A, B, C nằm trên đường tròn tâm O và các điểm M, N, P như Hình 4.54. Hãy chỉ ra ba cặp tam giác vuông bằng nhau trong hình.
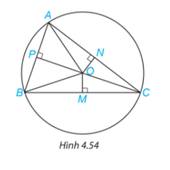
Vì A, B, C nằm trên đường tròn tâm O nên OA = OB = OC.
Xét hai tam giác ONA vuông tại N và ONC vuông tại N có:
OA = OC (cmt)
ON chung
Do đó ΔONA=ΔONC (cạnh huyền – cạnh góc vuông).
Xét hai tam giác OMB vuông tại M và OMC vuông tại M có:
OB = OC (cmt)
OM chung
Do đó ΔOMB=ΔOMC (cạnh huyền – cạnh góc vuông).
Xét hai tam giác OPA vuông tại P và OPB vuông tại P có:
OA = OB (cmt)
OP chung
Do đó ΔOPA=ΔOPB (cạnh huyền – cạnh góc vuông).
Hãy chỉ ra các cặp tam giác vuông đồng dạng với nhau trong Hình 9.52, viết đúng kí hiệu đồng dạng.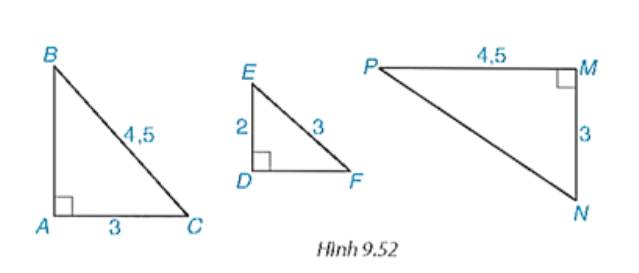
Ta có:
AC/BC = 3/4,5 = 2/3
DE/EF = 2/3
⇒ AC/BC = DE/EF
∆ABC và ∆DFE có:
AC/BC = DE/EF = 2/3
∠BAC = ∠EDF = 90⁰
⇒ ∆ABC ∽ ∆DFE (cạnh huyền - cạnh góc vuông)
Tam giác ABC và tam giác DEF có:
\( \widehat A = \widehat D = 90^0 \)
\( \frac {AC}{DE} = \frac {BC}{EF} = \frac {3}{2} \)
\( \Rightarrow \Delta ABC \backsim \Delta DFE (ch - cgv) \)
Hãy chỉ ra các cặp tam giác bằng nhau trong Hình 13 và cho biết chúng bằng nhau theo trường hợp nào.
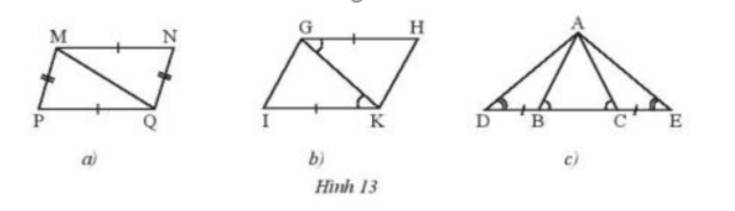
a) Ta thấy tam giác MNQ = tam giác MPQ (c-c-c)
b) Ta thấy tam giác GHK = tam giác GIK (c-g-c)
c) Ta thấy tam giác ADB = tam giác ACE (g-c-g)
Tam giác ADC = tam giác AEB (g-c-g)
Hãy chỉ ra các cặp tam giác bằng nhau trong Hình 22 và cho biết chúng bằng nhau theo trường hợp nào.
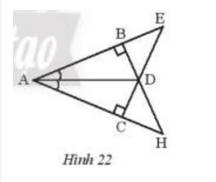
+) Xét \(\Delta{ABD}\) vuông tại B và \(\Delta{ACD}\) vuông tại D có:
AD chung
\(\widehat {BAD} = \widehat {DAC}\) (gt)
\( \Rightarrow \Delta{ABD}=\Delta{ACD}\) (cạnh huyền – góc nhọn)
\( \Rightarrow \) BD = CD, AB = AC ( 2 cạnh tương ứng)
\( \widehat {BDA} = \widehat {ADC}\)( 2 góc tương ứng)
+) Xét \(\Delta{BED}\) vuông tại B và \(\Delta{CHD}\) vuông tại C có:
BD = CD (cmt)
\(\widehat {BDE} = \widehat {CDH}\)( 2 góc đối đỉnh )
\( \Rightarrow \Delta{BED}=\Delta{CHD \) (cạnh góc vuông - góc nhọn kề )
+) Ta có: \(\widehat {BDA} + \widehat {BDE}\)= \(\widehat {ADE}\)
\(\widehat {ADC} + \widehat {CDH}\)= \(\widehat {ADH}\)
Mà \(\widehat {BDA} = \widehat {ADC}\), \(\widehat {BDE} = \widehat {CDH}\)
\( \Rightarrow \widehat {ADE} = \widehat {ADH}\)
Xét \(\Delta{ADE}\) và \(\Delta{ADH}\) có:
\(\widehat {BAD} = \widehat {DAC}\) (gt)
AD chung
\(\widehat {ADE} = \widehat {ADH}\) (cmt)
\( \Rightarrow \Delta{ADE}=\Delta{ADH}\)( g – c – g )
+) Xét \(\Delta{ABH}\) vuông tại B và \(\Delta{ACE}\) vuông tại C có:
AB = AC (cmt)
\(\widehat {BAH}\) chung
\( \Rightarrow \Delta{ABH}=\Delta{ACE}\) (cạnh góc vuông – góc nhọn kề)