Trong Hình 4.48, hãy tìm các cặp tam giác vuông bằng nhau và giải thích vì sao chúng bằng nhau.
QL
Những câu hỏi liên quan
Trong mỗi hình bên (H.4.39), hãy chỉ ra một cặp tam giác bằng nhau và giải thích vì sao chúng bằng nhau.

a)Xét \(\Delta ABD\) và \(\Delta CDB\) có:
AB=CD (gt)
\(\widehat {ABD} = \widehat {CDB}\) (gt)
BD chung
Vậy \(\Delta ABD = \Delta CDB\)(c.g.c)
b)Xét \(\Delta OAD\) và \(\Delta OCB\) có:
AO=CO (gt)
\(\widehat {AOD} = \widehat {COB}\) (đối đỉnh)
OD=OB (gt)
Vậy \(\Delta OAD = \Delta OCB\)(c.g.c)
Đúng 0
Bình luận (0)
Cho hình thang ABCD . Hai đáy là AB và CD . CD cắt nhau tại O . Hãy các cặp tam giác có diện tích bằng nhau và giải thích vì sao nó bằng nhau ?
Hai tam giác vuông ABC (vuông tại đỉnh A) và A’B’C’ (vuông tại đỉnh A’) có các cặp cạnh góc vuông bằng nhau: AB = A'B', AC = A'C' (H.4.45). Dựa vào trường hợp bằng nhau cạnh - góc - cạnh của hai tam giác, hãy giải thích vì sao hai tam giác vuông ABC và ABC bằng nhau.
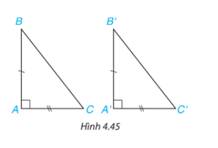
Xét 2 tam giác ABC và A’B’C có:
AB=A’B’ (gt)
\(\widehat A = \widehat {A'}\) (gt)
AC=A’C’ (gt)
\( \Rightarrow \Delta ABC = \Delta A'B'C'\)(c.g.c)
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD, hai đường chéo AC và BD cắt nhau tại O. Xét các tam giác có đỉnh lấy trong số các điểm A, B, C, O, hãy chỉ ra các tam giác có diện tích bằng nhau và giải thích vì sao.
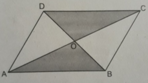
Xem hình bs.52.
- Các tam giác ADB, ACB, DAC, DBC có diện tích bằng nhau vì cùng bằng nửa diện tích hình bình hành đã cho.
- Các tam giác OAD, OCB, ODC, OBA có diện tích bằng nhau vì cùng bằng một phần tư diện tích hình bình hành đã cho.
Đúng 0
Bình luận (0)
Hãy chỉ ra các cặp tam giác bằng nhau trong Hình 13 và cho biết chúng bằng nhau theo trường hợp nào.
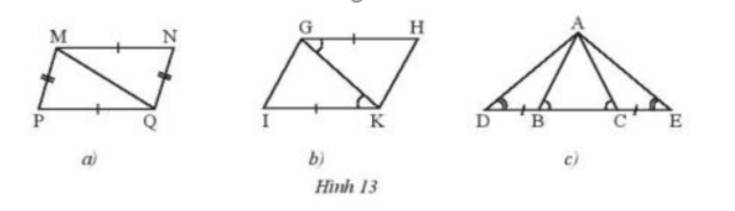
a) Ta thấy tam giác MNQ = tam giác MPQ (c-c-c)
b) Ta thấy tam giác GHK = tam giác GIK (c-g-c)
c) Ta thấy tam giác ADB = tam giác ACE (g-c-g)
Tam giác ADC = tam giác AEB (g-c-g)
Đúng 0
Bình luận (0)
Hãy chỉ ra các cặp tam giác bằng nhau trong Hình 22 và cho biết chúng bằng nhau theo trường hợp nào.
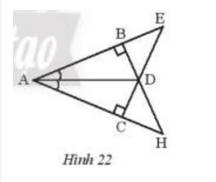
+) Xét \(\Delta{ABD}\) vuông tại B và \(\Delta{ACD}\) vuông tại D có:
AD chung
\(\widehat {BAD} = \widehat {DAC}\) (gt)
\( \Rightarrow \Delta{ABD}=\Delta{ACD}\) (cạnh huyền – góc nhọn)
\( \Rightarrow \) BD = CD, AB = AC ( 2 cạnh tương ứng)
\( \widehat {BDA} = \widehat {ADC}\)( 2 góc tương ứng)
+) Xét \(\Delta{BED}\) vuông tại B và \(\Delta{CHD}\) vuông tại C có:
BD = CD (cmt)
\(\widehat {BDE} = \widehat {CDH}\)( 2 góc đối đỉnh )
\( \Rightarrow \Delta{BED}=\Delta{CHD \) (cạnh góc vuông - góc nhọn kề )
+) Ta có: \(\widehat {BDA} + \widehat {BDE}\)= \(\widehat {ADE}\)
\(\widehat {ADC} + \widehat {CDH}\)= \(\widehat {ADH}\)
Mà \(\widehat {BDA} = \widehat {ADC}\), \(\widehat {BDE} = \widehat {CDH}\)
\( \Rightarrow \widehat {ADE} = \widehat {ADH}\)
Xét \(\Delta{ADE}\) và \(\Delta{ADH}\) có:
\(\widehat {BAD} = \widehat {DAC}\) (gt)
AD chung
\(\widehat {ADE} = \widehat {ADH}\) (cmt)
\( \Rightarrow \Delta{ADE}=\Delta{ADH}\)( g – c – g )
+) Xét \(\Delta{ABH}\) vuông tại B và \(\Delta{ACE}\) vuông tại C có:
AB = AC (cmt)
\(\widehat {BAH}\) chung
\( \Rightarrow \Delta{ABH}=\Delta{ACE}\) (cạnh góc vuông – góc nhọn kề)
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD, hai đường chéo AC và BD cắt nhau tại O. Xét các tam giác có đỉnh lấy trong số các điểm A, B, C, D, O. Hãy chỉ ra các tam giác có diện tích bằng nhau và giải thích vì sao ?
Ta có:
* SADB=SACB=SDAC=SDBC ( cùng bằng \(\dfrac{1}{2}.S_{hbh}\) )
* SOAD=SOCB=SODC=SOBA (cùng bằng \(\dfrac{1}{4}.S_{hbh}\))
Đúng 0
Bình luận (0)
Bài 8: Hãy chỉ ra các cặp tam giác bằng nhau trong và cho biết chúng bằng nhau theo trường hợp nào
Hình 1
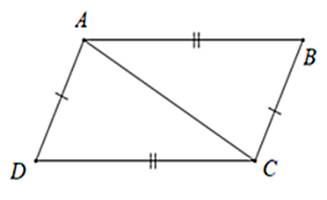
△ABC = △ADC (c.c.c) vì
AB = CD
AD = BC
AC chung
Đúng 1
Bình luận (0)
\(\Delta ABC=\Delta ADC\left(c.c.c\right)\)
Đúng 1
Bình luận (0)
Xét ΔABC và ΔADC có
+AB=DC (GT)
+AD=BC (GT)
+AC là cạnh chung
=> ΔABC=ΔADC (c.c.c)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC ( như hình vẽ )AM bằng 1/3 AB , AN bằng 1/3 AC .
a,Hãy tìm trong hình vẽ những cặp tam giác bằng nhau và giải thích .
b,Tính S tứ giác BMNC biết S tam giác ABC là 36 cm vuông
ai nhanh nhất mà có bài giải thì mik tick cho.






