Cho tam giác ABC vuông tại A. Tính tổng hai góc B và C.
QL
Những câu hỏi liên quan
1.Cho tam giác ABC có A + B = C + 90 và A = C + 10. Tính các góc của tam giác ABC
2.Cho tam giác ABC vuông tại A, vẽ các tia phân giác của B và C cắt nhau tại M. Tính BMC
3.Cho tam giác ABC có A =80, B = 60. Hai tia phân giác của B và c cắt nhau tại I, vẽ tia p/g góc ngoài tại B sao cho B cắt tia CI tại D
a) Tính BIC
b)CMR BDC = C
1, Ta có \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)(tổng 3 góc tam giác)
\(\Leftrightarrow\widehat{C}+90^o+\widehat{C}=180^o\)
\(\Leftrightarrow2\widehat{C}=90^o\)
\(\Leftrightarrow\widehat{C}=45^o\)
\(\Rightarrow\widehat{A}=\widehat{C}+10=55^o\)
\(\Rightarrow\widehat{B}=180^o-\widehat{A}-\widehat{C}=180^o-55^o-45^o=80^o\)
Đúng 0
Bình luận (0)
2,
Vì tam giác ABC vuông tại A
=> ^B + ^C = 90o
Vì BM là phân giác ^ABC
=>^B1 = \(\frac{\widehat{ABC}}{2}\)
Tương tự ^C1 = \(\frac{\widehat{ACB}}{2}\)
\(\Rightarrow\widehat{B_1}+\widehat{C_1}=\frac{\widehat{ABC}+\widehat{ACB}}{2}=\frac{90^o}{2}=45^o\)
Theo tổng 3 góc trong tam giác \(\widehat{BMC}=180^o-\widehat{B_1}-\widehat{C_1}=180^o-45^o=135^o\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, tính các góc B và góc C biết góc B bằng hai lần góc C
Trả lời:
tổng 2 góc B và C là: 180-90 =90 độ.
Vì góc B= 2 lần góc C
=> góc C= 30 độ và góc B= 60 độ.
ΔABC vuông tại A => B + C = 900 ( hai góc nhọn phụ nhau ) (1)
Lại có ^B = 2^C , thế vào (1) ta được 3^C = 900 => ^C = 300 => ^B = 600
Vậy ...
Xét ΔABC có: A= 90°
=> B + C = 90° ( định lí)
=> 2C + C = 90°
=> 3C = 90°
=> C = 30°
Do đó, B = 90° - 30° = 60°
Vậy....
1.Cho tam giác ABC cân tại B,biết góc A=40 độ. Tính hai góc B và C
2. Cho tam giác ABC vuông tại A, biết AB =6cm,BC=10cm.TÍnh chu vi tam giác ABC
3.cho tam giác ABC vuông tại A.BD là phân giác của góc B,vẽ DI vuông góc BC(điểm I thuộc BC)
Gọi K là giao điểm của 2 đường thẳng DI và AB.Chứng minh
a.tam giác ABD=tam giác IBD
b.BD vuông góc AI
c. DK=DC
d. Cho AB=6cm,AC=8cm.TÍnh IC
1.Cho tam giác ABC vuông tại A. Vẽ AH vuông góc với BC tại H. Chứng minh rằng góc B= góc HAC, góc C= góc BAH
2. Cho tam giác ABC có góc A=a. Hai tia phân giác của hai góc B,C cắt nhau tại I. Tính số đo góc BIC theo a.
Xét tam giác ABC có:
^A+^B+^C=180°(đl tổng ba góc tam giác)
=>^B+^C=180°-a
Vì BI là pg ^B
=>^ABI=^IBC=1/2^B
Vì CI là pg ^C
=>^BCI=^ICA=1/2^C
Ta có:^B+^C=180°-a
=>(^B+^C)/2=(180°-a)/2
=>^IBC+^BCI=90°-a/2
Xét tam giác BIC có:
^IBC+^BCI+^BIC=180°(đl tổng ba góc tam giác)
=>^BIC=180°-90°-a/2
=>^BIC=90°+a/2
Đúng 0
Bình luận (0)
Bạn vẽ hình giúp mình nhé. Mình chỉ giải thôi nha!
1.Vì AH vuông góc với BC
=>^AHC=90°
Xét tam giác HAC vuông tại H
=>^HAC+^C=90°
=>^HAC=90° -^C (1)
Xét tam giác ABC vuông tại A
=>^B+^C=90°
=>^B=90° - ^C (2)
Từ (1) và (2)=>đpcm
-----------------------------------------------------------------
Câu này cm tương tự
Đúng 0
Bình luận (0)
Để tối tớ lm câu hai nha bạn. H tớ phải đi học r ạ
Đúng 0
Bình luận (0)
1) Cho tam giác ABC vuông tại A có góc B = 60độ, AC = 3cm. Tính BC, AB
2) Cho tam giác ABC vuông tại A có BC = 10cm, góc C = 3cm. Tính góc B, AB, AC
3) Cho tam giác ABC vuông tại A có AB = 4cm, góc B = 50 độ. Tính BC, góc C, AC
3:
góc C=90-50=40 độ
Xét ΔABC vuông tại A có sin C=AB/BC
=>4/BC=sin40
=>\(BC\simeq6,22\left(cm\right)\)
\(AC=\sqrt{BC^2-AB^2}\simeq4,76\left(cm\right)\)
1:
góc C=90-60=30 độ
Xét ΔABC vuông tại A có
sin B=AC/BC
=>3/BC=sin60
=>\(BC=\dfrac{3}{sin60}=2\sqrt{3}\left(cm\right)\)
=>\(AB=\dfrac{2\sqrt{3}}{2}=\sqrt{3}\left(cm\right)\)
Đúng 0
Bình luận (1)
1) Cho tam iacs ABC , hai đg cao BD,CE cắt nhau tại H cho biết ACBH . C/m tam giác ABC có góc B 45 độ hoặc 135 độ2)dùng thước và compa để chia góc vuông cho trước thành 3 phần nhau 3)Cho tam giác ABC vuông cân tại A , qua A vê đg thẳng d thay đổi , ve BD và CE cùng vuông góc d (DE thuộ d). Cmr BD^2+CE^2 ko đổi4) Cho tam giác ABC có AB1 , góc A 75 độ , góc B 60 độ . Trên mửa mp BC có chứa A ve tia Bz sao cho góc CBz 15 độ a)C/m DC vuông góc BC b)Tính tổng BC^2+CD^25) Tam giác ABC vuông c...
Đọc tiếp
1) Cho tam iacs ABC , hai đg cao BD,CE cắt nhau tại H cho biết AC=BH . C/m tam giác ABC có góc B =45 độ hoặc 135 độ
2)dùng thước và compa để chia góc vuông cho trước thành 3 phần = nhau
3)Cho tam giác ABC vuông cân tại A , qua A vê đg thẳng d thay đổi , ve BD và CE cùng vuông góc d (DE thuộ d). Cmr BD^2+CE^2 ko đổi
4) Cho tam giác ABC có AB=1 , góc A =75 độ , góc B =60 độ . Trên mửa mp BC có chứa A ve tia Bz sao cho góc CBz =15 độ
a)C/m DC vuông góc BC
b)Tính tổng BC^2+CD^2
5) Tam giác ABC vuông cân tại A , trung tuyến AM (M tđ BC) . Cmr AE=CF
Xét 2 tam giác AEC và tam giác HEB có:
\(\widehat{AEC}=\widehat{HEB}\left(=90^o\right)\)
AC=BH (giả thiết)
\(\widehat{CAE}=\widehat{BHE}\left(=\widehat{DHC}\right)\)
\(\Rightarrow\Delta AEC=\Delta HEB\left(ch.gn\right)\)
=> EC=EB (2 cạnh tương ứng)
=> tam giác ECB cân tại E
=> \(\widehat{B}=45^o\)
Đây chỉ là TH góc B nhọn, còn TH góc B tù thì làm tương tự tìm ra góc B=135 độ
Đúng 0
Bình luận (0)
Lấy B thuộc Ox , A thuộc Oy sao cho OA=OB
Dùng compa vẽ đtron (O;OB) và (B;OB), 2 đường tròn cắt nhau tại D ,nối O với D
Dùng compa vẽ đtron (D;R) và (B;R) (với R là bán kính bất kì), 2 đtron cắt nhau tại H, nối O với H
OD và OH chia góc ra làm 3 phần bằng nhau
Đúng 0
Bình luận (0)
\(\widehat{BAD}=\alpha\Rightarrow\widehat{CAE}=90^o-\alpha\)
Ta có: Tam giác ABC vuông cân tại A => AB=AC
\(BD^2=\left(sin\left(\alpha\right).AB\right)^2=sin^2\alpha.AB^2\)
\(CE^2=\left(sin\left(90^o-\alpha\right).AC\right)^2=\left(cos\alpha.AC\right)^2=cos^2\alpha.AC^2\)
\(\Rightarrow BD^2+CE^2=sin^2\alpha.AB^2+cos^2a.AC^2=sin^2\alpha.AB^2+cos^2\alpha.AB^2=AB^2\left(sin^2\alpha+cos^2\alpha\right)=AB^2\)
Do AB không đổi nên BD2+CE2 không đổi (đpcm)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
a. Tam giác ABC vuông tại A biết góc C = 40°. Tính góc B.
b. Tam giác MNP cân tại M và góc M = 75°. Tính số đo hai góc N và P
a. tam giác ABC vg tại A suy ra B+C=90 suy ra B=90-40=50
b. từ đề bài suy ra N+P=180-75=105 và N=P=(N+P)/2=......
Cho hình chóp S. ABC có đáy là tam giác ABC đều cạnh a, tam giác SBA vuông tại B, tam giác SAC vuông tại C. Biết góc giữa hai mặt phẳng (SAB) và (ABC) bằng
60
0
. Tính khoảng cách từ điểm C đến mặt phẳng (SAB).
Đọc tiếp
Cho hình chóp S. ABC có đáy là tam giác ABC đều cạnh a, tam giác SBA vuông tại B, tam giác SAC vuông tại C. Biết góc giữa hai mặt phẳng (SAB) và (ABC) bằng 60 0 . Tính khoảng cách từ điểm C đến mặt phẳng (SAB).
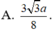
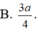
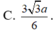
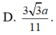
Chọn đáp án B
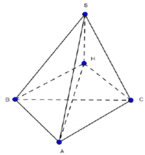
Gọi là H hình chiếu của đỉnh S xuống mặt phẳng (ABC). Khi đó, ta có
![]()
Ta có
![]()
Tương tự, ta cũng chứng minh được
![]()
Từ đó suy ra
![]()
Do SH ⊥ AB, BH ⊥ AB nên suy ra góc giữa (SAB) và (ABC) là góc SBH. Vậy SBH = 60 0
![]()
Trong tam giác vuông ABH, ta có
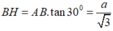
Trong tam giác vuông SHB, ta có
![]()
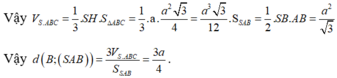
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AC=3cm, AB=4cm, BC=5cm. a)Chứng minh tam giác ABC vuông. Tính góc B và C b) Phân giác của góc A cắt BC tại D. Tính BD và CD.
a) Xét ΔABC có
\(BC^2=AB^2+AC^2\left(5^2=3^2+4^2\right)\)
nên ΔABC vuông tại A(Định lí Pytago đảo)
Xét ΔABC vuông tại A có
\(\sin\widehat{C}=\dfrac{AB}{BC}=\dfrac{4}{5}\)
nên \(\widehat{C}\simeq53^0\)
\(\Leftrightarrow\widehat{B}=37^0\)
b) Xét ΔABC có AD là đường phân giác ứng với cạnh BC(gt)
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)
hay \(\dfrac{BD}{4}=\dfrac{CD}{3}\)
mà BD+CD=5
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{4}=\dfrac{CD}{3}=\dfrac{BD+CD}{4+3}=\dfrac{5}{7}\)
Do đó: \(BD=\dfrac{20}{7}cm;CD=\dfrac{15}{7}cm\)
Đúng 0
Bình luận (0)



