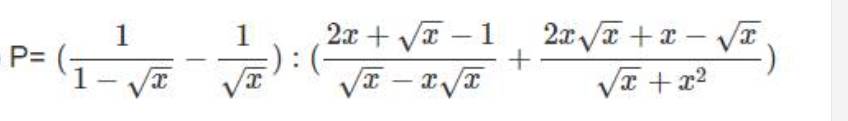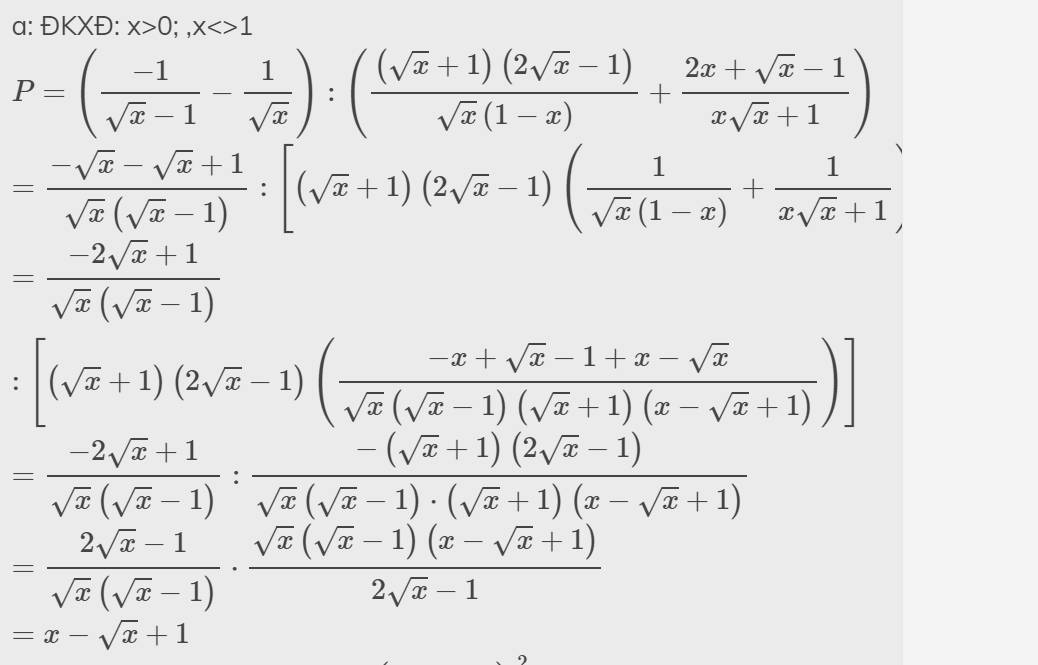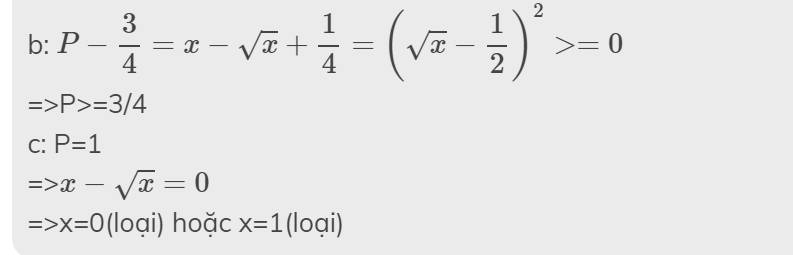a, \(x+1\ge0\Leftrightarrow x\ge-1\)

b, \(1-2x\ge0\Leftrightarrow x\le\dfrac{1}{2}\)

c, \(\left\{{}\begin{matrix}x+1\ge0\\x-2\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge-1\\x\ge2\end{matrix}\right.\Leftrightarrow x\ge2\)

d, \(\left\{{}\begin{matrix}2-3x\ge0\\1-2x\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\le\dfrac{2}{3}\\x\le\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow x\le\dfrac{1}{2}\)

e, \(\left\{{}\begin{matrix}\sqrt{3}-2x\ge0\\x-1\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\le\dfrac{\sqrt{3}}{2}\\x\ne1\end{matrix}\right.\Leftrightarrow x\le\dfrac{\sqrt{3}}{2}\)

f, \(\left\{{}\begin{matrix}x-\dfrac{\sqrt{3}}{2}\ge0\\x\ge0\\\sqrt{x}-1\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{\sqrt{3}}{2}\\x\ge0\\x\ne1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{\sqrt{3}}{2}\\x\ne1\end{matrix}\right.\)

g, \(\left\{{}\begin{matrix}\sqrt{x}-1\ne0\\\sqrt{x}+2\ne0\\x\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x\ne1\end{matrix}\right.\)

1: \(\Leftrightarrow\dfrac{3x-1}{x+2}=4\)

=>4x+8=3x-1

=>x=-9

2: \(\Leftrightarrow\dfrac{5x-7}{2x-1}=4\)

=>8x-4=5x-7

=>3x=-3

=>x=-1

3: ĐKXD: x>=0

\(PT\Leftrightarrow\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)=\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)\)

=>\(x+\sqrt{x}-6=x-1\)

=>căn x=-1+6=5

=>x=25

4: ĐKXĐ: x>=0

PT =>\(\left(\sqrt{x}-3\right)\left(\sqrt{x}+1\right)=\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)\)

=>x-2*căn x-3=x-4

=>-2căn x-3=-4

=>2căn x+3=4

=>2căn x=1

=>căn x=1/2

=>x=1/4

\(a,\dfrac{-5}{x+6}\ge0\\ mà\left(-5< 0\right)\\ \Rightarrow x+6< 0\\ \Rightarrow x< -6\\ b,\dfrac{2}{6-x}\ge0\\ mà\left(2>0\right)\\ \Rightarrow6-x>0\\ \Rightarrow x< 6\\ c,\dfrac{-x+3}{-6}\ge0\\ mà-6< 0\\ \Rightarrow-x+3< 0\\ \Rightarrow x>3\\\)

\(d,\dfrac{7x-1}{-9}\ge0\\mà-9< 0\\ \Rightarrow 7x-1\le0\\ \Rightarrow x\le\dfrac{1}{7}\\ e,\dfrac{x+2}{x^2+2x+1}\ge0\\ mà\left(x^2+2x+1\right)>0\forall x\\ \Rightarrow x+2\ge0\\ \Rightarrow x\ge-2\\ f,\dfrac{x-2}{x^2-2x+4}\ge0\\ mà\left(x^2-2x+4\right)>0\forall x\\ \Rightarrow x-2\ge0\\ \Rightarrow x\ge2\)

Chứng minh : \(x^2-2x+4>0\\ x^2-2x+1+3=\left(x-1\right)^2+3\ge3>0\)

a: ĐKXĐ: \(\dfrac{-5}{x+6}>=0\)

=>x+6<0

=>x<-6

b: ĐKXĐ: (-2)/(6-x)>=0

=>6-x<0

=>x>6

c: ĐKXĐ: (-x+3)/(-6)>=0

=>-x+3<=0

=>-x<=-3

=>x>=3

d: ĐKXĐ: (7x-1)/-9>=0

=>7x-1<=0

=>x<=1/7

e: ĐKXĐ: (x+2)/(x^2+2x+1)>=0

=>x+2>=0

=>x>=-1

f: ĐKXĐ: (x-2)/(x^2-2x+4)>=0

=>x-2>=0

=>x>=2

a: ĐKXĐ: x^2-2x<>0 và x^2-1>0

=>(x>1 và x<>2) hoặc x<-1

b: ĐKXĐ: x+1>0 và 5-3x>0

=>x>-1 và 3x<5

=>-1<x<5/3

c: DKXĐ: 5x+3>=0 và 3-x>0

=>x>=-3/5 và x<3

=>-3/5<=x<3

d: ĐKXĐ: 4-x^2>0 và 1+x>=0

=>x^2<4 và x>=-1

=>-2<x<2 và x>=-1

=>-1<=x<2

e: ĐKXĐ: 2-3x<>0 và 1-6x>0

=>x<>2/3 và x<1/6

=>x<1/6

1) ĐKXĐ: \(x\ge-2\)

\(pt\Leftrightarrow\dfrac{\sqrt{x+2}}{2}+5\sqrt{x+2}-2\sqrt{x+2}=14\)

\(\Leftrightarrow\dfrac{\sqrt{x+2}+6\sqrt{x+2}}{2}=14\Leftrightarrow7\sqrt{x+2}=28\)

\(\Leftrightarrow\sqrt{x+2}=4\Leftrightarrow x+2=16\Leftrightarrow x=14\left(tm\right)\)

2) ĐKXĐ: \(x\ge0\)

\(pt\Leftrightarrow2x+3=x^2\Leftrightarrow\left(x-3\right)\left(x+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=3\left(tm\right)\\x=-1\left(ktm\right)\end{matrix}\right.\)

3) \(pt\Leftrightarrow\sqrt{\left(5x+2\right)^2}=1\Leftrightarrow\left|5x+2\right|=1\)

\(\Leftrightarrow\left[{}\begin{matrix}5x+2=1\\5x+2=-1\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{5}\\x=-\dfrac{3}{5}\end{matrix}\right.\)

4) ĐKXĐ: \(\left[{}\begin{matrix}\left\{{}\begin{matrix}x+1\ge0\\2x-1>0\end{matrix}\right.\\\left\{{}\begin{matrix}x+1\le0\\2x-1< 0\end{matrix}\right.\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x>\dfrac{1}{2}\\x\le-1\end{matrix}\right.\)

\(pt\Leftrightarrow\dfrac{x+1}{2x-1}=4\Leftrightarrow x+1=8x-4\)

\(\Leftrightarrow7x=5\Leftrightarrow x=\dfrac{5}{7}\left(tm\right)\)

5) ĐKXĐ: \(x\ge2\)

\(pt\Leftrightarrow\dfrac{x-2}{3x+1}=36\)

\(\Leftrightarrow x-2=108x+36\Leftrightarrow107x=-38\Leftrightarrow x=-\dfrac{38}{107}\left(ktm\right)\)

Vậy \(S=\varnothing\)

Sửa đề: 

`a)sqrt{x^2-2x+1}=2`

`<=>sqrt{(x-1)^2}=2`

`<=>|x-1|=2`

`**x-1=2<=>x=3`

`**x-1=-1<=>x=-1`.

Vậy `S={3,-1}`

`b)sqrt{x^2-1}=x`

Điều kiện:\(\begin{cases}x^2-1 \ge 0\\x \ge 0\\\end{cases}\)

`<=>` \(\begin{cases}x^2 \ge 1\\x \ge 0\\\end{cases}\)

`<=>x>=1`

`pt<=>x^2-1=x^2`

`<=>-1=0` vô lý

Vậy pt vô nghiệm

`c)sqrt{4x-20}+3sqrt{(x-5)/9}-1/3sqrt{9x-45}=4(x>=5)`

`pt<=>sqrt{4(x-5)}+sqrt{9*(x-5)/9}-sqrt{(9x-45)*1/9}=4`

`<=>2sqrt{x-5}+sqrt{x-5}-sqrt{x-5}=4`

`<=>2sqrt{x-5}=4`

`<=>sqrt{x-5}=2`

`<=>x-5=4`

`<=>x=9(tmđk)`

Vậy `S={9}.`

`d)x-5sqrt{x-2}=-2(x>=2)`

`<=>x-2-5sqrt{x-2}+4=0`

Đặt `a=sqrt{x-2}`

`pt<=>a^2-5a+4=0`

`<=>a_1=1,a_2=4`

`<=>sqrt{x-2}=1,sqrt{x-2}=4`

`<=>x_1=3,x_2=18`,

`e)2x-3sqrt{2x-1}-5=0`

`<=>2x-1-3sqrt{2x-1}-4=0`

Đặt `a=sqrt{2x-1}(a>=0)`

`pt<=>a^2-3a-4=0`

`a-b+c=0`

`<=>a_1=-1(l),a_2=4(tm)`

`<=>sqrt{2x-1}=4`

`<=>2x-1=16`

`<=>x=17/2(tm)`

Vậy `S={17/2}`

d.

ĐKXĐ: $x\geq 2$. Đặt $\sqrt{x-2}=a(a\geq 0)$ thì pt trở thành:

$a^2+2-5a=-2$

$\Leftrightarrow a^2-5a+4=0$

$\Leftrightarrow (a-1)(a-4)=0$

$\Rightarrow a=1$ hoặc $a=4$

$\Leftrightarrow \sqrt{x-2}=1$ hoặc $\sqrt{x-2}=4$

$\Leftrightarrow x=3$ hoặc $x=18$ (đều thỏa mãn)

e. ĐKXĐ: $x\geq \frac{1}{2}$

Đặt $\sqrt{2x-1}=a(a\geq 0)$ thì pt trở thành:

$a^2+1-3a-5=0$

$\Leftrightarrow a^2-3a-4=0$

$\Leftrightarrow (a+1)(a-4)=0$

Vì $a\geq 0$ nên $a=4$

$\Leftrightarrow \sqrt{2x-1}=4$

$\Leftrightarrow x=\frac{17}{2}$

a.

$\sqrt{x^2-2x+1}=2$

$\Leftrightarrow \sqrt{(x-1)^2}=2$

$\Leftrightarrow |x-1|=2$

$\Rightarrow x-1=\pm 2$

$\Leftrightarrow x=3$ hoặc $x=-1$ (đều thỏa mãn)

b. ĐKXĐ: $x\geq 1$ hoặc $x\leq -1$

PT \(\Rightarrow \left\{\begin{matrix} x\geq 0\\ x^2-1=x^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq 0\\ 1=0\end{matrix}\right.\) (vô lý)

Vậy pt vô nghiệm

c. ĐKXĐ: $x\geq 5$

PT $\Leftrightarrow \sqrt{4(x-5)}+3\sqrt{\frac{x-5}{9}}-\frac{1}{3}\sqrt{9(x-5)}=4$

$\Leftrightarrow 2\sqrt{x-5}+\sqrt{x-5}-\sqrt{x-5}=4$

$\Leftrightarrow 2\sqrt{x-5}=4$

$\Leftrightarrow \sqrt{x-5}=2$

$\Leftrightarrow x=2^2+5=9$ (thỏa mãn)

$A=2x-\sqrt{x}=2(x-\frac{1}{2}\sqrt{x}+\frac{1}{4^2})-\frac{1}{8}$

$=2(\sqrt{x}-\frac{1}{4})^2-\frac{1}{8}$

$\geq \frac{-1}{8}$

Vậy $A_{\min}=-\frac{1}{8}$. Giá trị này đạt tại $x=\frac{1}{16}$

$B=x+\sqrt{x}$

Vì $x\geq 0$ nên $B\geq 0+\sqrt{0}=0$

Vậy $B_{\min}=0$. Giá trị này đạt tại $x=0$

Vì $2-x\geq 0$ (theo ĐKXĐ) nên $C=1+\sqrt{2-x}\geq 1$

Vậy $C_{\min}=1$. Giá trị này đạt tại $2-x=0\Leftrightarrow x=2$

1) ĐKXĐ: \(x^2+2x-3\ge0\Leftrightarrow\left(x+1\right)^2\ge4\)

\(\Leftrightarrow\left[{}\begin{matrix}x+1\ge2\\x+1\le-2\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x\ge1\\x\le-3\end{matrix}\right.\)

2) ĐKXĐ: \(2x^2+5x+3\ge0\Leftrightarrow2\left(x+\dfrac{5}{4}\right)^2\ge\dfrac{1}{8}\Leftrightarrow\left(x+\dfrac{5}{4}\right)^2\ge\dfrac{1}{16}\)

\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{5}{4}\ge\dfrac{1}{4}\\x+\dfrac{5}{4}\le-\dfrac{1}{4}\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x\ge-1\\x\le-\dfrac{3}{2}\end{matrix}\right.\)

3) ĐKXĐ: \(x-1>0\Leftrightarrow x>1\)

4) ĐKXĐ: \(x-3< 0\Leftrightarrow x< 3\)

5) ĐKXĐ: \(x+2< 0\Leftrightarrow x< -2\)

6) ĐKXĐ: \(2a-1>0\Leftrightarrow a>\dfrac{1}{2}\)

Lời giải:
a.

\(\left\{\begin{matrix} x\neq 0\\ 2x-1\geq 0\\ x^2-3x+2=(x-1)(x-2)\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\neq 0\\ x\geq \frac{1}{2}\\ x\neq 1; x\neq 2\end{matrix}\right.\)

$\Leftrightarrow x\geq \frac{1}{2}; x\neq 1; x\neq 2$
b. \(\left\{\begin{matrix} x^2-1=(x-1)(x+1)\neq 0\\ 7-2x\geq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\neq \pm 1\\ x\leq \frac{7}{2}\end{matrix}\right.\)

c.

\(\left\{\begin{matrix} x\neq 0\\ 4-2x+x^2\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\neq 0\\ (x-1)^2+3\neq 0\end{matrix}\right.\Leftrightarrow x\neq 0\)

d.

\(\left\{\begin{matrix} 25-x^2=(5-x)(5+x)\geq 0\\ x\geq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} -5\leq x\leq 5\\ x\geq 0\end{matrix}\right.\Leftrightarrow 0\leq x\leq 5\)

a) \(y=\dfrac{1}{x}-\dfrac{\sqrt[]{2x-1}}{x^2-3x+2}\)

Điều kiện \(\) \(2x-1\ge0;x\ne0;x^2-3x+2\ne0\)

\(\Leftrightarrow x\ge\dfrac{1}{2};x\ne0;\left(x-1\right)\left(x-2\right)\ne0\)

\(\Leftrightarrow x\ge\dfrac{1}{2};x\ne0;x\ne1;x\ne2\)

a) \(x\ge\dfrac{1}{2};x\ne1;x\ne2\)

b) \(x\le\dfrac{7}{2};x\ne\pm1\)

c) \(x\ne0\)

d) \(0\le x\le5\)