Gọi tên các mặt bên và mặt đáy của hình chóp.
QL
Những câu hỏi liên quan
Cho hình chóp S.ABCD. Gọi tên các mặt bên và mặt đáy của hình chóp đó.
- Các mặt bên: (SAB), (SBC), (SCD), (SAD).
- Mặt đáy: ABCD.
Đúng 0
Bình luận (0)
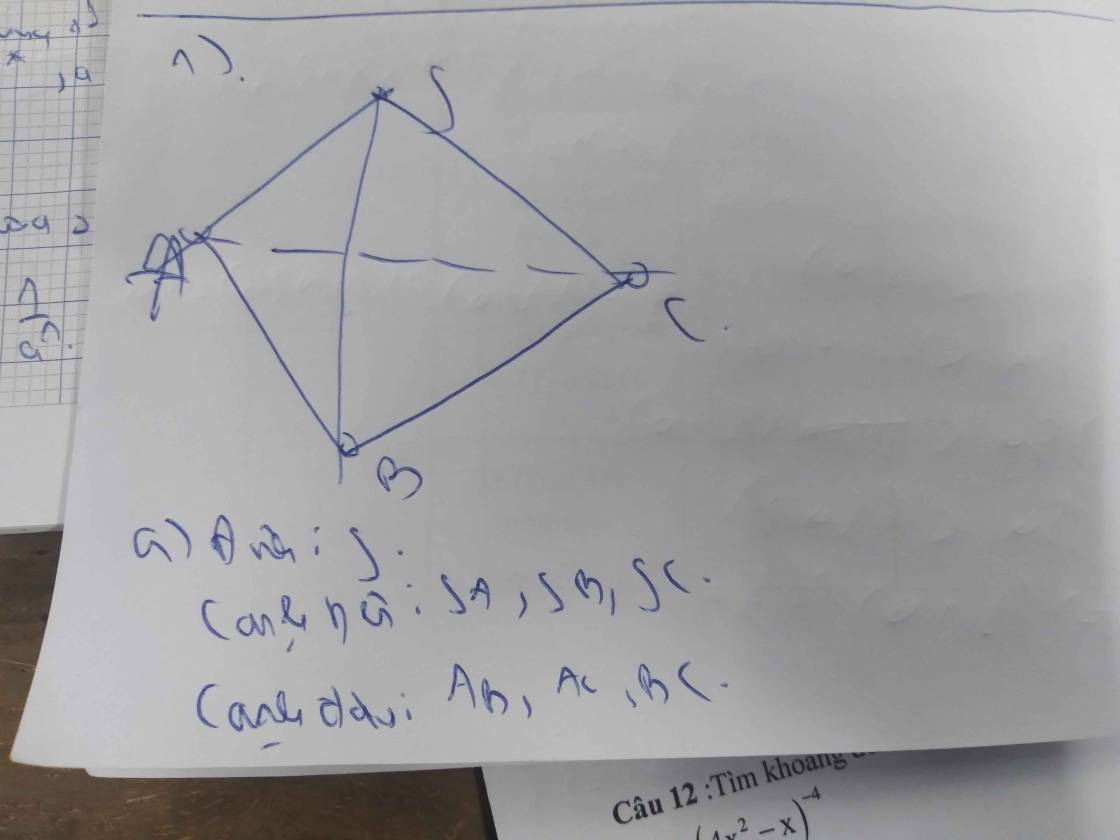
1) cho hình chóp S.ABC, đáy ABC là tam giáca) kể tên đỉnh, các cạnh bên, cạnh đáy, mặt bên và mặt đáy của hình chópb) tìm giao tuyến của hai mặt phẳng (SBC) và (ABC)c) tìm giao tuyến của 2 mặt phẳng (SAB) và (SBC)2) cho hình chóp S.MNP, đáy MNP là tam giáca) kể tên đỉnh, các cạnh bên, cạnh đáy, mặt bên và mặt đáy của hình chópb) tìm giao tuyến của hai mặt phẳng (SMN) và (MNP)c) tìm giao tuyến của 2 mặt phẳng (SMP) và (SNP)
Đọc tiếp
1) cho hình chóp S.ABC, đáy ABC là tam giác
a) kể tên đỉnh, các cạnh bên, cạnh đáy, mặt bên và mặt đáy của hình chóp
b) tìm giao tuyến của hai mặt phẳng (SBC) và (ABC)
c) tìm giao tuyến của 2 mặt phẳng (SAB) và (SBC)
2)
cho hình chóp S.MNP, đáy MNP là tam giác
a) kể tên đỉnh, các cạnh bên, cạnh đáy, mặt bên và mặt đáy của hình chóp
b) tìm giao tuyến của hai mặt phẳng (SMN) và (MNP)
c) tìm giao tuyến của 2 mặt phẳng (SMP) và (SNP)
1) cho hình chóp S.ABC, đáy ABC là tam giáca) kể tên đỉnh, các cạnh bên, cạnh đáy, mặt bên và mặt đáy của hình chópb) tìm giao tuyến của hai mặt phẳng (SBC) và (ABC)c) tìm giao tuyến của 2 mặt phẳng (SAB) và (SBC)2) cho hình chóp S.MNP, đáy MNP là tam giáca) kể tên đỉnh, các cạnh bên, cạnh đáy, mặt bên và mặt đáy của hình chópb) tìm giao tuyến của hai mặt phẳng (SMN) và (MNP)c) tìm giao tuyến của 2 mặt phẳng (SMP) và (SNP)
Đọc tiếp
1) cho hình chóp S.ABC, đáy ABC là tam giác
a) kể tên đỉnh, các cạnh bên, cạnh đáy, mặt bên và mặt đáy của hình chóp
b) tìm giao tuyến của hai mặt phẳng (SBC) và (ABC)
c) tìm giao tuyến của 2 mặt phẳng (SAB) và (SBC)
2)
cho hình chóp S.MNP, đáy MNP là tam giác
a) kể tên đỉnh, các cạnh bên, cạnh đáy, mặt bên và mặt đáy của hình chóp
b) tìm giao tuyến của hai mặt phẳng (SMN) và (MNP)
c) tìm giao tuyến của 2 mặt phẳng (SMP) và (SNP)
Cho hình chóp S.ABC, đáy ABC là tam giác: a) Đỉnh: S Các cạnh bên: SA, SB, SC Cạnh đáy: AB, BC, CA Mặt bên: SAB, SBC, SCA Mặt đáy: ABC b) Giao tuyến của hai mặt phẳng (SBC) và (ABC) là cạnh SB. c) Giao tuyến của hai mặt phẳng (SAB) và (SBC) là cạnh SC. Cho hình chóp S.MNP, đáy MNP là tam giác: a) Đỉnh: S Các cạnh bên: SM, SN, SP Cạnh đáy: MN, NP, PM Mặt bên: SMN, SNP, SMP Mặt đáy: MNP b) Giao tuyến của hai mặt phẳng (SMN) và (MNP) là cạnh SN. c) Giao tuyến của hai mặt phẳng (SMP) và (SNP) là cạnh SP.
Đúng 0
Bình luận (0)
cho hình chóp S.MNPQ, đáy MNPQ là hình chữ nhật
a) kể tên đỉnh, các cạnh bên, cạnh đáy, mặt bên và mặt đáy của hình chóp
b) tìm giao tuyến của hai mặt phẳng (SPQ) và (MNPQ)
c) tìm giao tuyến của 2 mặt phẳng (SMQ) và (SQP)
1.cho hình chóp S.MNPQ, đáy MNPQ là hình chữ nhật
a) kể tên đỉnh, các cạnh bên, cạnh đáy, mặt bên và mặt đáy của hình chóp
b) tìm giao tuyến của hai mặt phẳng (SPQ) và (MNPQ)
c) tìm giao tuyến của 2 mặt phẳng (SMQ) và (SQP)
Một)- Đỉnh của hình chóp S.MNPQ là điểm S.- Các cạnh bên của hình chóp là SM, SN, NP, NQ, PQ.- Cạnh đáy của hình chóp là đoạn thẳng MN, NP, PQ và QM.- Mặt bên của hình chóp là tam giác SMN, SNP, NQP và QMS.- Mặt đáy của hình chóp là hình chữ nhật MNPQ.b) Giao tuyến của hai mặt phẳng (SPQ) và (MNPQ) là một đường thẳng. Gọi đường thẳng này là d.c) Giao tuyến của hai mặt phẳng (SMQ) và (SQP) cũng là một đường thẳng. Gọi đường thẳng này là e.
Đúng 0
Bình luận (0)
cho hình chóp S.MNP, đáy MNP là tam giác
a) kể tên đỉnh, các cạnh bên, cạnh đáy, mặt bên và mặt đáy của hình chóp
b) tìm giao tuyến của hai mặt phẳng (SMN) và (MNP)
c) tìm giao tuyến của 2 mặt phẳng (SMP) và (SNP)
a) Trong hình chóp S.MNP, các thành phần được kể tên như sau:
Đỉnh: SCác cạnh bên: SM, SN, SPCạnh đáy: MNPMặt bên: Các mặt tam giác SMN, SNP, SMPMặt đáy: Tam giác MNPb) Để tìm giao tuyến của hai mặt phẳng (SMN) và (MNP), chúng ta cần tìm đường thẳng giao của hai mặt phẳng này. Đường thẳng này chính là đường thẳng chứa đường chéo của tam giác MNP, vì đường chéo của tam giác nằm trên mặt phẳng (SMN) và (MNP) cùng một lúc.
c) Để tìm giao tuyến của hai mặt phẳng (SMP) và (SNP), chúng ta cũng cần tìm đường thẳng giao của hai mặt phẳng này. Đường thẳng này chính là đường thẳng chứa cạnh SP của tam giác SNP và cạnh SP của tam giác SMP, vì cả hai cạnh này nằm trên mặt phẳng (SMP) và (SNP) cùng một lúc.
Đúng 0
Bình luận (0)
cho hình chóp S.MNP, đáy MNP là tam giác
a) kể tên đỉnh, các cạnh bên, cạnh đáy, mặt bên và mặt đáy của hình chóp
b) tìm giao tuyến của hai mặt phẳng (SMN) và (MNP)
c) tìm giao tuyến của 2 mặt phẳng (SMP) và (SNP)
a: Đỉnh: S
Cạnh bên: SM,SN,SP
Cạnh đáy: MN,MP,NP
Mặt bên: SNP,SMP,SNM
Mặt đáy: MNP
b: \(MN\subset\left(SMN\right)\)
\(MN\subset\left(MNP\right)\)
Do đó: \(\left(SMN\right)\cap\left(MNP\right)=MN\)
c: \(SP\subset\left(SMP\right)\)
\(SP\subset\left(SNP\right)\)
Do đó: \(\left(SMP\right)\cap\left(SNP\right)=SP\)
Đúng 1
Bình luận (0)
Kể tên các mặt bên, cạnh bên, cạnh đáy của hình chóp ở hình 2.24.

- Hình chóp tam giác:
Các mặt bên: (SAB), (SBC), (SAC)
Các cạnh bên: SA, SB, SC
Các cạnh đáy: AB, AC, BC
- Hình chóp tứ giác:
Các mặt bên: (SAB), (SBC), (SCD), (SAD)
Các cạnh bên: SA, SB, SC, SD
Các cạnh đáy: AB, BC, CD, DA
Đúng 0
Bình luận (0)
Quan sát và gọi tên các mặt đáy, mặt bên, cạnh đáy, cạnh bên của hình lăng trụ đứng tam giác ở hình 10.31.
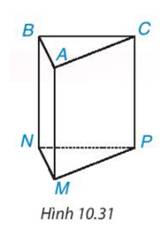
+ 2 mặt đáy : ABC, MNP
+ 3 mặt bên : ACPM, BAMN, BCPN
+ Cạnh đáy : NM, MP, NP, AB, BC, CA
+ Cạnh bên : AM, BN, CP
Đúng 0
Bình luận (0)
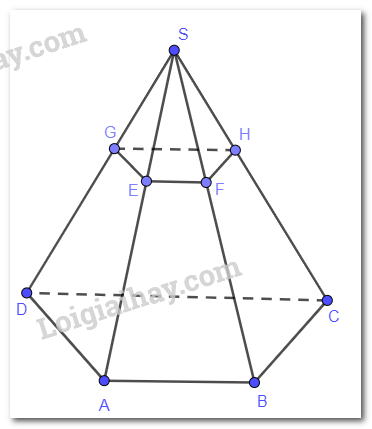
Cho hình chóp S.ABCD có đáy là hình thang (AB//CD). Gọi E là một điểm nằm giữa S và A. Gọi (P) là mặt phẳng qua E và song song với hai đường thẳng AB, AD. Xác định giao tuyến của (P) và các mặt bên của hình chóp. Hình tạo bởi các giao tuyến là hình gì?
Mặt phẳng (SAD) chứa đường thẳng AD song song với mp(P) nên mặt phẳng (P) cắt (SAD) theo giao tuyến song song với AD. Vẽ EG // AD (G thuộc SD) thì EG là giao tuyến của (P) và (SAD).
Mặt phẳng (SAB) chứa đường thẳng AB song song với mp(P) nên mặt phẳng (P) cắt (SAB) theo giao tuyến song song với AB. Vẽ EF // AB (F thuộc SB) thì EF là giao tuyến của (P) và (SAB).
Ta có AB // CD, EF // AB suy ra CD // EF hay CD // mp(P)
Mặt phẳng (SCD) chứa đường thẳng CD song song với mp(P) nên mặt phẳng (P) cắt (SCD) theo giao tuyến song song với CD. Vẽ GH // CD (H thuộc SC) thì GH là giao tuyến của (P) và (SCD).
FH thuộc (P), FH thuộc (SBC) suy ra FH là giao tuyến của (P) và (SBC).
Tứ giác EFGH có EF // GH (vì cùng song song với CD) suy ra EFGH là hình thang.
Đúng 0
Bình luận (0)