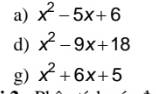
nhân tử chung
Cho phân thức:
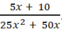
a) Phân tích tử và mẫu thành nhân tử rồi tìm nhân tử chung của chúng.
b) Chia cả tử và mẫu cho nhân tử chung.
a) 5x + 10 = 5(x + 2)
25x2 + 50x = 25x(x + 2)
⇒ Nhân tử chung của chúng là: 5(x + 2)
b)
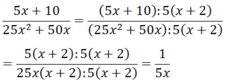
Cho phân thức:
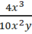
a) Tìm nhân tử chung của cả tử và mẫu.
b) Chia cả tử và mẫu cho nhân tử chung.
a) Nhân tử chung của cả tử và mẫu: 2x2
b)
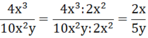
phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung:
-x2-4xy-4y2
= \(-\left(x^2+4xy+4y^2\right)\)
= \(-\left(x+2y\right)^2\)
Biến đa thức thành nhân tử bằng phowung pháp đặt nhân tử chung.
3xy-21x2y2
3x2y-5xy2+7xy
\(3xy-21x^2y^2=3xy\left(1-7xy\right)\)
\(3x^2y-5xy^2+7xy\)
\(=xy\left(3x-5y+7\right)\)
\(3xy-21x^2y^2\\ =3xy-3xy.7xy\\ =3xy\left(1-7xy\right)\)
Cái thứ hai không phân tích bằng đặt nhân tử chung được đâu nha=)
85.12,7+5.3.12,7 Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
85.12,7+5.3.12,7=12,7.(85+5.3)=12,7.(85+15)=12,7.100=1270
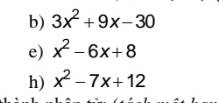
đặt nhân tử chung
h: =3(x^2+3x-10)
=3(x^2+5x-2x-10)
=3[x(x+5)-2(x+5)]
=3(x+5)(x-2)
e: =x^2-2x-4x+8
=x(x-2)-4(x-2)
=(x-2)(x-4)
h: =x^2-3x-4x+12
=x(x-3)-4(x-3)
=(x-3)(x-4)
Lời giải:
b. $3x^2+9x-30=3(x^2+3x-10)$
$=3[(x^2-2x)+(5x-10)]=3[x(x-2)+5(x-2)]=3(x-2)(x+5)$
e. $x^2-6x+8=(x^2-2x)-(4x-8)=x(x-2)-4(x-2)=(x-4)(x-2)$
h. $x^2-7x+12=(x^2-3x)-(4x-12)=x(x-3)-4(x-3)=(x-3)(x-4)$
-2a^2(x-1)+4a(1-x) phân tích thành nhân tử bằng phương pháp đặt nhân tử chung
= (-2a ^2 +4a)(1-x)
= -2 (a^2 -2a)(1-x)
= -2a(a-2)(1-x)
= 2a(a-2)(x-1)
\(-2a^2\left(x-1\right)+4a\left(1-x\right)\)
\(=-a\cdot2a\left(x-1\right)-2\cdot2a\left(x-1\right)\)
\(=2a\left(x-1\right)\left(-a-2\right)\)
Cho 4 x n + 2 – 8 x n (n Є N*). Khi đặt nhân tử chung x n ra ngoài thì nhân tử còn lại là
A. 4 x 2 – 2
B. 4 x 2 – 8
C. x 2 – 4
D. x 2 – 2
Ta có 4 x n + 2 – 8 x n = 4 x n . x 2 – 8 x n = x n ( 4 x 2 – 8 )
Vậy khi đặt nhân tử chung x n ra ngoài ta được biểu thức còn lại là 4 x 2 – 8
Đáp án cần chọn là: B