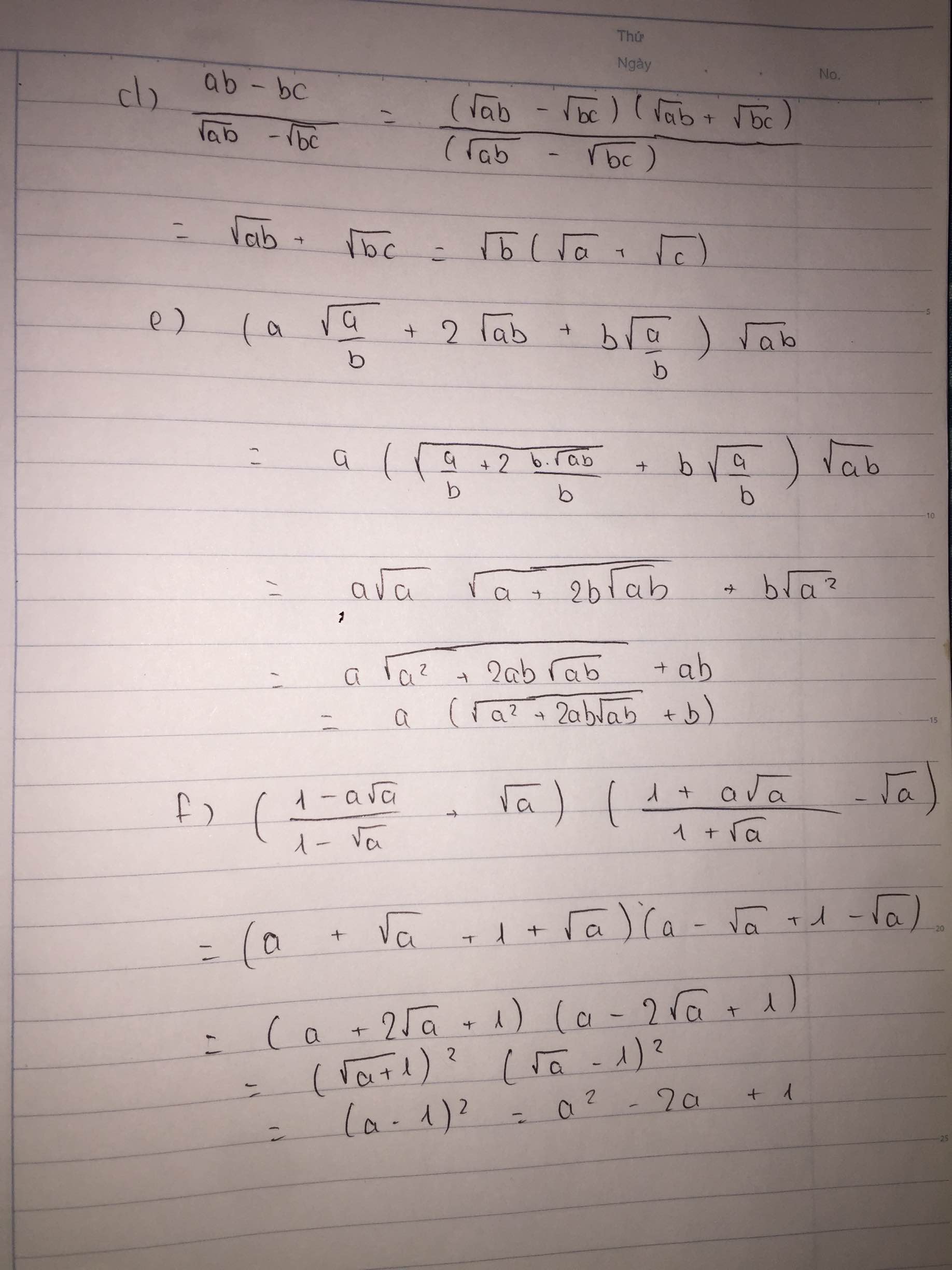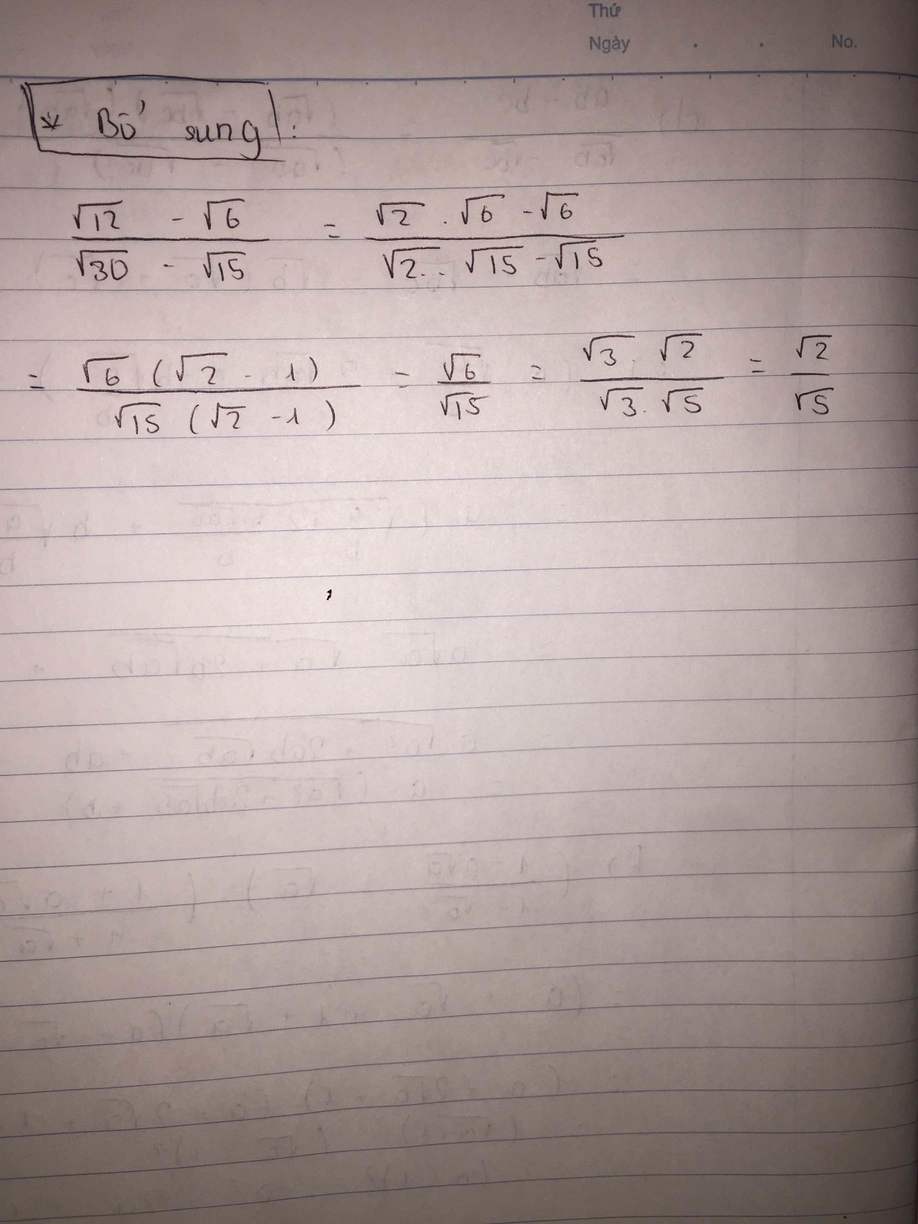j, ĐK: \(x\ne\dfrac{\pi}{6}+\dfrac{k\pi}{2}\)

\(tan\left(\dfrac{\pi}{3}+x\right)-tan\left(\dfrac{\pi}{6}+2x\right)=0\)

\(\Leftrightarrow tan\left(\dfrac{\pi}{3}+x\right)=tan\left(\dfrac{\pi}{6}+2x\right)\)

\(\Leftrightarrow\dfrac{\pi}{3}+x=\dfrac{\pi}{6}+2x+k\pi\)

\(\Leftrightarrow x=\dfrac{\pi}{6}+k\pi\left(l\right)\)

\(\Rightarrow\) vô nghiệm.

\(b,\dfrac{\sqrt{12}-\sqrt{6}}{\sqrt{30}-\sqrt{15}}=\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{\sqrt{15}\left(\sqrt{2}-1\right)}=\dfrac{\sqrt{6}}{\sqrt{15}}=\dfrac{\sqrt{2}}{\sqrt{5}}\)

\(d,\dfrac{ab-bc}{\sqrt{ab}-\sqrt{bc}}=\dfrac{\left(\sqrt{ab}-\sqrt{bc}\right)\left(\sqrt{ab}+\sqrt{bc}\right)}{\left(\sqrt{ab}-\sqrt{bc}\right)}=\sqrt{ab}+\sqrt{bc}=\sqrt{b}\left(\sqrt{a}+\sqrt{c}\right)\)

\(e,\left(a\sqrt{\dfrac{a}{b}+2\sqrt{ab}}+b\sqrt{\dfrac{a}{b}}\right)\sqrt{ab}\)

\(=a\left(\sqrt{\dfrac{a}{b}+\dfrac{2b.\sqrt{ab}}{b}}+b\sqrt{\dfrac{a}{b}}\right)\sqrt{ab}\)

\(=a\sqrt{a}\sqrt{a+2b\sqrt{ab}}+b\sqrt{a^2}\)

\(=a\sqrt{a^2+2ab\sqrt{ab}}+ab\)

\(=a\left(\sqrt{a^2+2ab\sqrt{ab}}+b\right)\)

\(f,\left(\dfrac{1-a\sqrt{a}}{1-\sqrt{a}}+\sqrt{a}\right)\left(\dfrac{1+a\sqrt{a}}{1+\sqrt{a}}-\sqrt{a}\right)\)

\(=\left(a+\sqrt{a}+1+\sqrt{a}\right)\left(a-\sqrt{a}+1-\sqrt{a}\right)\)

\(=\left(a+2\sqrt{a}+1\right)\left(a-2\sqrt{a}+1\right)\)

\(=\left(\sqrt{a}+1\right)^2\left(\sqrt{a}-1\right)^2\)

\(=\left(a-1\right)^2=a^2-2a+1\)

Gợi ý cho em cách viết:

Giới thiệu khái quát về món ăn.

Nguồn gốc?

Cách chế biến?

Ý nghĩa của món ăn đó với mọi người hoặc với em?

Nêu cảm nhận của em về món ăn đó?

Kết luận. 

b.

\(\Leftrightarrow\dfrac{1}{2}cosx-\dfrac{\sqrt{3}}{2}sinx=-\dfrac{1}{2}\)

\(\Leftrightarrow cos\left(x+\dfrac{\pi}{3}\right)=-\dfrac{1}{2}\)

\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{3}=\dfrac{2\pi}{3}+k2\pi\\x+\dfrac{\pi}{3}=-\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k2\pi\\x=-\pi+k2\pi\end{matrix}\right.\)

c.

\(\Leftrightarrow\dfrac{3}{5}sinx-\dfrac{4}{5}cosx=1\)

Đặt \(\dfrac{3}{5}=cosa\) với \(a\in\left(0;\dfrac{\pi}{2}\right)\Rightarrow\dfrac{4}{5}=sina\)

Pt trở thành:

\(sinx.cosa-cosx.sina=1\)

\(\Leftrightarrow sin\left(x-a\right)=1\)

\(\Leftrightarrow x-a=\dfrac{\pi}{2}+k2\pi\)

\(\Leftrightarrow x=a+\dfrac{\pi}{2}+k2\pi\)

d.

\(\Leftrightarrow\dfrac{\sqrt{2}}{2}sinx-\dfrac{\sqrt{2}}{2}cosx=\dfrac{\sqrt{2}}{2}\)

\(\Leftrightarrow sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\)

\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{4}=\dfrac{\pi}{4}+k2\pi\\x-\dfrac{\pi}{4}=\dfrac{3\pi}{4}+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k2\pi\\x=\pi+k2\pi\end{matrix}\right.\)

Ta có: \(\frac{x+2}{y+10}\)\(=\)\(\frac{1}{5}\)\(\Rightarrow\)\(5\left(x+2\right)=y+10\)(1)

             \(y-3x=2\)\(\Rightarrow\)\(y+2=3x\)                              (2)

Thay (2) vào (1) ta có:

\(5\left(x+2\right)=\left(y+2\right)+8\)

\(5x+10=3x+8\)

\(5x-3x=8-10\)

\(2x=-2\)

\(x=-2:2\)

\(x=-1\)

Vậy: x=-1

Chúc bạn làm bài tốt!