Chứng minh các phương trình sau đây vô nghiệm:
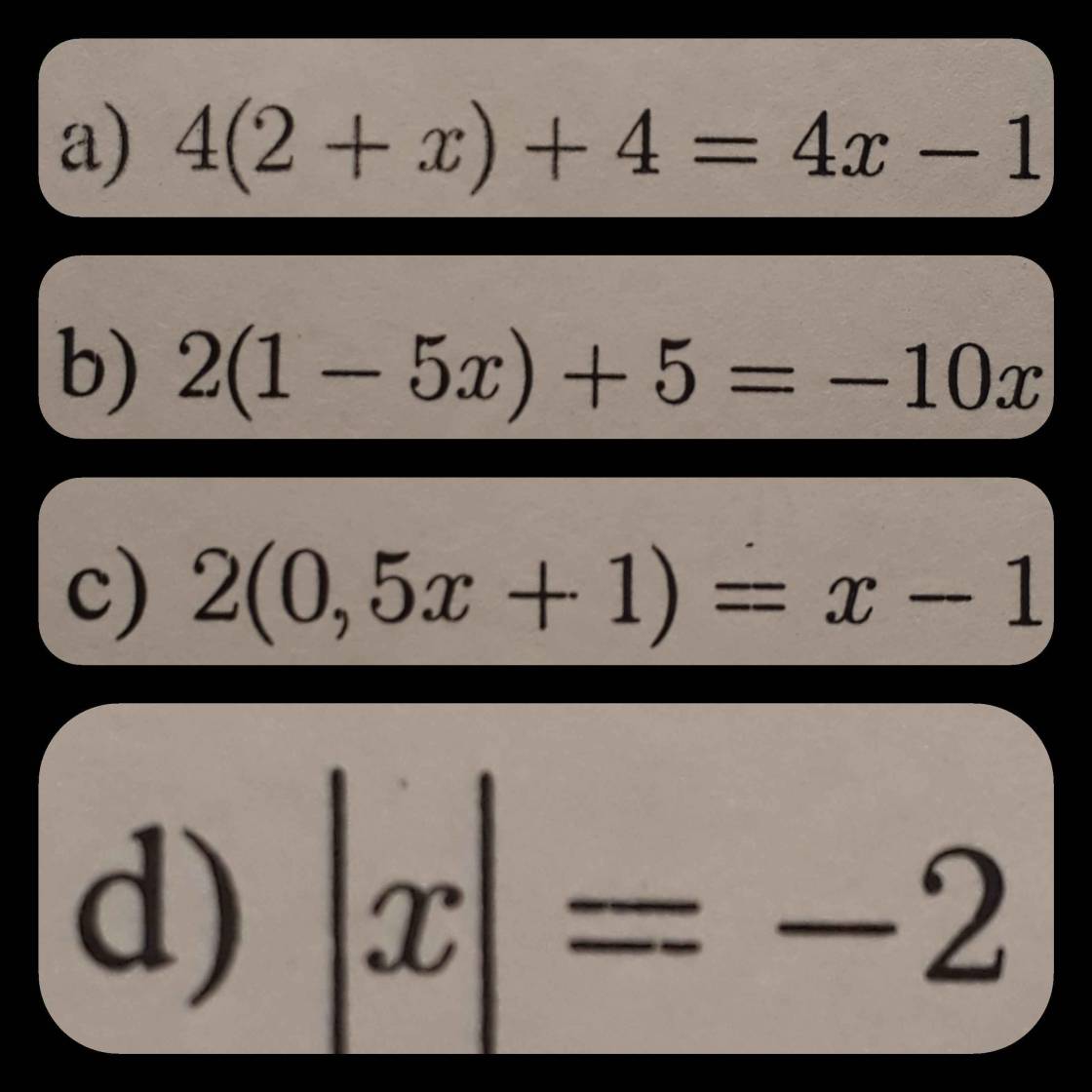
Chứng minh rằng phương trình sau đây vô nghiệm :
\(2x^2-3x+9\)
Ta có : \(2x^2-3x+9=0\)
\(\Leftrightarrow\left(x\sqrt{2}\right)^2-2.x\sqrt{2}.\dfrac{3}{2\sqrt{2}}+\dfrac{9}{8}+\dfrac{63}{8}=0\)
\(\Leftrightarrow\left(x\sqrt{2}-\dfrac{3}{2\sqrt{2}}\right)^2+\dfrac{63}{8}=0\)
\(\Leftrightarrow\left(x\sqrt{2}-\dfrac{3}{2\sqrt{2}}\right)^2=-\dfrac{63}{8}\) ( Vô lý )
Vậy phương trình vô nghiệm .
Ta có: \(2x^2-3x+9=0\)
\(\Leftrightarrow\left(x^2-2x+1\right)+\left(x^2-x+\dfrac{1}{4}\right)+\dfrac{31}{4}=0\)
\(\Leftrightarrow\left(x-1\right)^2+\left(x-\dfrac{1}{2}\right)^2+\dfrac{31}{4}=0\)
\(\Leftrightarrow\left(x-1\right)^2+\left(x-\dfrac{1}{2}\right)^2=-\dfrac{31}{4}\) ( Vô lí )
Vậy phương trình vô nghiệm.
Chứng tỏ rằng các phương trình sau đây vô nghiệm: |x| = -1
Vì |x| ≥ 0 nên phương trình |x| = -1 vô nghiệm.
chứng minh rằng các phương trình sau đây vô nghiệm : \(5\sin2x+\sin x+\cos x+6=0\)
chứng minh rằng các phương trình sau đây vô nghiệm : \(5\sin2x+\sin x+\cos x+6=0\)
Chứng tỏ rằng các phương trình sau đây vô nghiệm: 2(1 – 1,5x) + 3x = 0
Ta có: 2(1 – 1,5x) + 3x = 0 ⇔ 2 – 3x + 3x = 0 ⇔ 2 + 0x = 0
Vậy phương trình vô nghiệm.
Chứng tỏ rằng các phương trình sau đây vô nghiệm: 2(x + 1) = 3 + 2x
Ta có: 2(x + 1) = 3 + 2x ⇔ 2x + 2 = 3 + 2x ⇔ 0x = 1
Vậy phương trình vô nghiệm.
Chứng minh các phương trình sau vô nghiệm:
a) (x-2)3=(x-2).(x2+2x+4)-6.(x-1)2
b)4x2-12x+10=0
Chứng minh các phương trình sau vô số nghiệm:
(x+1).(x2-x-1)=(x+1)3-3x.(x+1)
\(\text{CM vô nghiệm}\)
\(\text{a) }\left(x-2\right)^3=\left(x-2\right).\left(x^2+2x+4\right)-6\left(x-1\right)^2\)
\(\Leftrightarrow x^3-6x^2+12x-8=x^3-8-6\left(x^2-2x+1\right)\)
\(\Leftrightarrow x^3-6x^2+12x-8=x^3-8-6x^2+12x-6\)
\(\Leftrightarrow x^3-6x^2+12x-x^3+6x-12x=-8+8-6\)
\(\Leftrightarrow0x=-6\text{ (vô lí)}\)
\(\text{Vậy }S=\varnothing\)
\(\text{b) }4x^2-12x+10=0\)
\(\Leftrightarrow\left(4x^2-12x+9\right)+1=0\)
\(\Leftrightarrow\left(2x-3\right)^2+1=0\)
\(\Leftrightarrow\left(2x-3\right)^2=-1\text{ (vô lí)}\)
\(\text{Vậy }S=\varnothing\)
\(\text{CM vô số nghiệm}\)
\(\left(x+1\right)\left(x^2-x+1\right)=\left(x+1\right)^3-3x\left(x+1\right)\)
\(\Leftrightarrow\left(x+1\right)\left(x^2-x+1\right)=\left(x+1\right)\left[\left(x+1\right)^2-3x\right]\)
\(\Leftrightarrow\left(x+1\right)\left(x^2-x+1\right)=\left(x+1\right)\left(x^2+2x+1-3x\right)\)
\(\Leftrightarrow\left(x+1\right)\left(x^2-x+1\right)=\left(x+1\right)\left(x^2-x+1\right)\text{ (luôn luôn đúng)}\)
\(\text{Vậy }S\inℝ\)
Chứng minh bất phương trình sau vô nghiệm: x 2 + x + 8 ≤ - 3
Điều kiện xác định x ≥ –8
Ta có: 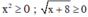 nên
nên 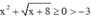 với mọi x ≥ –8.
với mọi x ≥ –8.
Do đó BPT 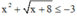 vô nghiệm.
vô nghiệm.
Chứng minh bất phương trình sau vô nghiệm: 1 + x 2 - 7 + x 2 > 1