6x^2 - 16x + 6 = 0 giải phương trình ạ
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
TN
Những câu hỏi liên quan
BÀI 1. Giải các phương trình sau bằng công thức nghiệm hoặc (công thức nghiện thu gọn). 1) x2 - 11x + 38 = 0 ; 2) 6x2 + 71x + 175 = 0 ; 3) 5x2 - 6x + 27 = 0 ; 4) - 30x2 + 30x - 7,5 = 0 ; 5) 4x2 - 16x + 17 = 0 ; 6) x2 + 4x - 12 = 0 ;
1, \(\Delta=\left(-11\right)^2-4.1.38=121-152=-31< 0\)
\(\Rightarrow\) pt vô nghiệm
2, \(\Delta=71^2-4.6.175=5041-4200=841\)
\(x_1=\dfrac{-71+\sqrt{841}}{2.6}=\dfrac{-71+29}{12}=\dfrac{-42}{12}=-\dfrac{7}{2}\)
\(x_2=\dfrac{-71-\sqrt{841}}{2.6}=\dfrac{-71-29}{12}=\dfrac{-10}{12}=-\dfrac{25}{3}\)
3, \(\Delta=\left(-3\right)^2-5.27=9-135=-126< 0\)
⇒ pt vô nghiệm
4, \(\Delta=15^2-\left(-30\right)\left(-7,5\right)=225-225=0\)
\(\Rightarrow x_1=x_2=\dfrac{-30}{2.\left(-30\right)}=\dfrac{1}{2}\)
5, \(\Delta'=\left(-8\right)^2-4.17=64-68=-4\)
⇒ pt vô nghiệm
6, \(\Delta=4^2-4.1.\left(-12\right)=16+48=64\)
\(x_1=\dfrac{-4+\sqrt{64}}{2.1}=\dfrac{-4+8}{2}=\dfrac{4}{2}=2\)
\(x_2=\dfrac{-4-\sqrt{64}}{2.1}=\dfrac{-4-8}{2}=\dfrac{-12}{2}=-6\)
Đúng 1
Bình luận (1)
Giải phương trình
a, x4 + 5x3 + 12x2 +20x + 16 = 0
b, 16x4 - 24x3 + 16x2 - 6x + 1 = 0
giải các phương trình sau:
a) x4−2x3−6x+16x−8=0
Giải phương trình:
\(4x^2-6x+1=-\dfrac{\sqrt{3}}{3}.\sqrt{16x^4+4x^2+1}\)
Ta có:
\(16x^4+4x^2+1=16x^4+8x^2+1-4x^2=\left(4x^2+1\right)^2-4x^2=\left(4x^2-2x+1\right)\left(4x^2+2x+1\right)\)
\(4x^2-6x+1=2\left(4x^2-2x+1\right)-\left(4x^2+2x+1\right)\)
Chia hai vế phương trình ban đầu cho \(4x^2+2x+1\) ta được
\(2\dfrac{4x^2-2x+1}{4x^2+2x+1}-1=\dfrac{-\sqrt{3}}{3}\sqrt{\dfrac{4x^2-2x+1}{4x^2+2x+1}}\)
Đặt \(y=\sqrt{\dfrac{4x^2-2x+1}{4x^2+2x+1}}>0\), phương trình trên tương đương với
\(2y^2-1=\dfrac{-\sqrt{3}}{3}y\Leftrightarrow\left[{}\begin{matrix}y=\dfrac{\sqrt{3}}{3}\left(tm\right)\\y=\dfrac{-\sqrt{3}}{2}\left(l\right)\end{matrix}\right.\)
Với \(y=\dfrac{\sqrt{3}}{3}\) ta có:
\(\dfrac{4x^2-2x+1}{4x^2+2x+1}=\dfrac{1}{3}\Leftrightarrow3\left(4x^2-2x+1\right)-\left(4x^2+2x+1\right)=0\)
\(\Leftrightarrow x=\dfrac{1}{2}\).
Đúng 1
Bình luận (0)
Giải các bất phương trình mũ sau: 16 x - 4 x - 6 ≤ 0
Đặt t = 4 x (t > 0), ta có hệ bất phương trình:
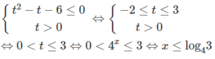
Đúng 0
Bình luận (0)
Giải phương trình (x2+16x+60)(x2+17x+60)=6x2
giải phương trình : (x2 + 16x + 60 ) ( x2 + 17x + 60 ) = 6x2
đặt x2 + 16x + 60 = t thì PT đã cho trở thành :
t ( t + x ) - 6x2 = 0 \(\Leftrightarrow\)t2 + xt - 6x2 = 0
\(\Leftrightarrow\)( t - 2x ) ( t + 3x ) = 0 \(\Leftrightarrow\)\(\orbr{\begin{cases}t=2x\\t=-3x\end{cases}}\)
+) t = 2x thì x2 + 16x + 60 = 2x \(\Leftrightarrow\)x2 + 14x + 60 = 0 ( vô nghiệm )
+) t = -3x thì x2 + 16x + 60 = -3x \(\Leftrightarrow\)x2 + 19x + 60 = 0
\(\Leftrightarrow\)\(\orbr{\begin{cases}x=-4\\x=-15\end{cases}}\)
Vậy ....
giải phương trình sau :
\(\sqrt{2x-2}-\sqrt{6x-9}=16x^2-48x+35\)
(ĐK : x>= 3/2)
nhận 2 vế của pt với \(\sqrt{2}tađược\):
\(\sqrt{2.\left(2x-2\right)}-\sqrt{2.\left(6x-9\right)}=\sqrt{2}.\left(16x^2-48x+35\right)\)
<=> \(\left(\sqrt{4x-4}-\sqrt{3}\right)-\left(\sqrt{12x-18}-\sqrt{3}\right)=\sqrt{2}.\left(4x-7\right).\left(4x-5\right)\)
<=> \(\left(\frac{4x-7}{\sqrt{4x-4}+\sqrt{3}}\right)-\left(\frac{12x-21}{\sqrt{12x-18}+\sqrt{3}}\right)=\sqrt{2}.\left(4x-7\right).\left(4x-5\right)\)
<=>\(\left(4x-7\right).\left(\frac{1}{\sqrt{4x-4}+\sqrt{3}}-\frac{3}{\sqrt{12x-18}+\sqrt{3}}-\sqrt{2}.\left(4x-5\right)\right)=0\)
<=> (4x-7) .g(x) = 0
<=> x = 7/4(tm) hoặc g(x)= 0
+) với g(x) = 0 <=> \(\left(\frac{1}{\sqrt{4x-4}+\sqrt{3}}-\frac{3}{\sqrt{12x-18}+\sqrt{3}}-\sqrt{2}.\left(4x-5\right)\right)=0\) <=> \(\left(\frac{1}{\sqrt{4x-4}+\sqrt{3}}-\frac{3}{\sqrt{12x-18}+\sqrt{3}}-\sqrt{2}.\left(4x-6\right)-\sqrt{2}\right)=0\)
<=>\(\left(\frac{1-\sqrt{2}.\sqrt{4x-4}-\sqrt{2}.\sqrt{3}}{\sqrt{4x-4}+\sqrt{3}}-\frac{3}{\sqrt{12x-18}+\sqrt{3}}-\sqrt{2}.\left(4x-6\right)\right)=0\) vô nghiện vì VT < 0 với mọi x >= 2/3 ...
VẬY X = 7/4 ... nếu đúng thì like nhé !!!
Đúng 0
Bình luận (0)
Giải phương trình \(x^6-6x^5+15x^4-20x^3+15x^2-6x+1=0\)
\(x^6-6x^5+15x^4-20x^3+15x^2-6x+1=0\)
\(\Leftrightarrow x^6-x^5-5x^5+5x^4+10x^4-10x^3-10x^3+10x^2+5x^2-5x-x+1=0\)
\(\Leftrightarrow x^5\left(x-1\right)-5x^4\left(x-1\right)+10x^3\left(x-1\right)-10x^2\left(x-1\right)+5x\left(x-1\right)-\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^5-5x^4+10x^3-10x^2+5x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left[x^5-x^4-4x^4+4x^3+6x^3-6x^2-4x^2+4x+x-1\right]=0\)
\(\Leftrightarrow\left(x-1\right)\left[x^4\left(x-1\right)-4x^3\left(x-1\right)+6x^2\left(x-1\right)-4x\left(x-1\right)+x-1\right]=0\)
\(\Leftrightarrow\left(x-1\right)^2\left[x^4-4x^3+6x^2-4x+1\right]=0\)
\(\Leftrightarrow\left(x-1\right)^2\left[x^4-x^3-3x^3+3x^2+3x^2-3x-x+1\right]=0\)
\(\Leftrightarrow\left(x-1\right)^3\left[x^3-3x^2+3x-1\right]=0\)
\(\Leftrightarrow\left(x-1\right)^3\left[x^3-x^2-2x^2+2x+x-1\right]=0\)
\(\Leftrightarrow\left(x-1\right)^4\left[x^2-2x+1\right]=0\Leftrightarrow\left(x-1\right)^6=0\Leftrightarrow x=1\)
Đúng 1
Bình luận (0)




