cho▲ABC vuông tại A,biếtAB=18cm,AC=24cm 3 đg trung tuyến AM,BN,CP cắt nhau tại G.Tính:AM,GM,GA
H24
Những câu hỏi liên quan
cho tam giác abc có 3 đường trung tuyến am,bn và cp. các đoạn thẳng cp và bn cắt nhau tại g.biết rằng ga=4cm, gb=gc=6cm
a. tính độ dài các đường trung tuyến của tam giác abc.
b. chứng minh tam giác abc cân
Cho tam giác HPG có 3 trung tuyến HM,PA,GB cắt nhau tại T . Biết TH = 3 cm,TP=TG=4 cm a, Tính HM,PA,GB. b, Chứng minh tam giác HPG cân
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A. Đg p/g của góc BAC cắt BC tại M. a) Đg trung tuyến BN cắt AM tại G (N thuộc AC). Tính BN, biết AM = 9cm, BC = 8cm b) Kẻ đg thẳng đi qua C và vuông góc với BC, cắt tia BN tại E. Cm góc AEB > góc ABE
CHO TAM GIÁC ABC BIẾT GÓC A = 90 ĐỘ , AB=6CM , AC=8CM. CÁC ĐƯỜNG TRUNG TUYẾN AM , BN, CP CẮT NHAU TẠI G
a, TÍNH BC, BN, CP
b, TÍNH GA
CÁC PN CỐ GẮNG GIÚP MK VS !! CẢM ƠN CÁC PN NHÌU LÉM
a, áp dụng định lý pytago đối với tam giá vuông abc tao có mk chỉ làm dc phân a thôi phần b vẫn chưa
BC2 = AB2 + AC2 nghĩ ra bạn ak
BC2= 62 + 82
BC2=36+64
BC2=100
BC=căn bậc 2 của 100 và bằng 10
Đúng 0
Bình luận (0)
Cho ∆ABC có 3 đường trung tuyến AM, BN và CP. Các đoạn thẳng CP và BN cắt nhau tại điểm G. biết rằng GA=4cm, GB=GC=6 cm.
a)Tính độ dài các đường trung tuyến của ∆ABC
b) CM ∆ABC cân
Cho tam giác abc có ba đường trung tuyến AM,BN,CP cắt nhau tại G. Chứng minh rằng:
AM+BN+CP<AB+AC+BC
giúp em với ạ, em cảm ơn nhiều :
cho tam giác abc có 3 đường trung tuyến AM,BN,CP. Các đoạn thẳng CP và BN cắt nhau tại G. biết GA = 4cm. GB=GC=6cm
a) tính độ dài các đường trung tuyến của tam giác ABC
b)chứng minh tam giác ABC cân
mk pit làm phần a thui
vì AG=2GM
+) AG=4 cm
=>4=2GM
=> MG=4:2=2 (cm)
+)gm+ag=am
+)mg=2 cm
+) ag=9cm
=>2+9=am
=> am=11 cm
tính độ dài đoạn cp và bn tương tự như trên
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A có AB=24cm ,AC=18cm, đg trung trực BC cắt BC tại M,BAtại E,CA tại D.
TÍNH:BC,BE,CD.
cho tam giác ABC cân tại A trung tuyến AM và trung tuyến BN cắt nhau tại G
Qua C kẻ đường thẳng vuông góc với BC và cắt BN tại I
a chứng minh tam giác AGB = AGC
b c/m rằng GM bằn 1/2 CI
c so sánh AIB và ABI
a: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao và AM cũng là phân giác
Xét ΔABG và ΔACG có
AB=AC
\(\widehat{BAG}=\widehat{CAG}\)
AG chung
Do đó: ΔABG=ΔACG
b: Xét ΔBIC có
M là trung điểm của BC
MG//IC
Do đó: G là trung điểm của BI
Xét ΔBIC có
M là trung điểm của BC
G là trung điểm của BI
Do đó: MG là đường trung bình
=>MG=1/2CI
Đúng 5
Bình luận (0)
Cho tam giác ABC. Ba đường trung tuyến AM, BN, CP đồng quy tại G. Chứng minh:
\(GA + GB + GC = \dfrac{2}{3}(AM + BN + CP)\).
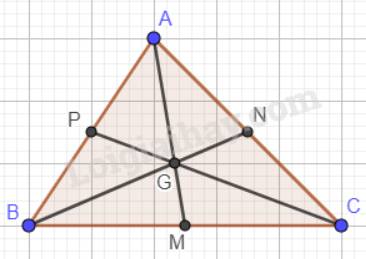
Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng \(\dfrac{2}{3}\)độ dài đường trung tuyến đi qua đỉnh ấy nên:
\(\begin{array}{l}\dfrac{{GA}}{{AM}} = \dfrac{{GB}}{{BN}} = \dfrac{{GC}}{{CP}} = \dfrac{2}{3}\\ \to GA = \dfrac{2}{3}AM;GB = \dfrac{2}{3}BN;GC = \dfrac{2}{3}CP\end{array}\)
Vậy:
\(GA + GB + GC = \dfrac{2}{3}AM + \dfrac{2}{3}BN + \dfrac{2}{3}CP = \dfrac{2}{3}(AM + BN + CP)\).
Đúng 0
Bình luận (0)



