Tìm GTNN của A=2(x-1)^2-2024
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
AN
Những câu hỏi liên quan
Tìm GTNN
A=x^2-20x+2024
A = \(x^2\) - 20\(x\) + 2024
A = (\(x^2\) - 20\(x\) + 100) + 1924
A = (\(x\) - 10)2 + 1924
Vì ( \(x-10\))2 ≥ 0 ⇒ (\(x-10\))2 + 1924 ≥ 1924
Vậy Amin = 1924 ⇔ \(x\) = 10
Kết luận giá trị nhỏ nhất của A là 1924 xảy ra khi \(x\) = 10
Đúng 1
Bình luận (0)
Cho x,y>0 thỏa mãn: \(x+2y\le5\)
Tìm gtnn của biểu thức:
\(P=x^2+2y^2-2x-9y+\dfrac{1}{x}+\dfrac{4}{y}+2024\)
Tìm GTNN của P= x2+2y2+2xy-6x-8y+2024
tìm GTNN của \(P=x^2+2y^2+2xy-6x-8y+2024\)
\(P=x^2+2y^2+2xy-6x-8y+2024\)
\(P=x^2+y^2+y^2+2xy-6x-6y-2y+2024\)
\(P=\left(x^2+2xy+y^2\right)-\left(6x+6y\right)+9+y^2-2y+1+2014\)
\(P=\left(x+y\right)^2-2\left(x+y\right)3+3^2+\left(y^2-2y+1\right)+2014\)
\(P=\left(x+y-3\right)^2+\left(y-1\right)^2+2014\)
\(P\ge2014\forall x;y\)
Dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}x+y-3=0\\y-1=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=2\\y=1\end{cases}}}\)
Vậy.....
Đúng 0
Bình luận (0)
Tìm gtnn của bt sau :
D=9x^2+y^2+6(xy-x)-4y+2024
tìm GTNN của \(P=|x-2020|+|x-2022|+|x-2024|\)
Lời giải:
Áp dụng BĐT dạng $|a|+|b|\geq |a+b|$ ta có:
$|x-2020|+|x-2024|=|x-2020|+|2024-x|\geq |x-2020+2024-x|=4$
$|x-2022|\geq 0$ (theo tính chất trị tuyệt đối)
$\Rightarrow |x-2020|+|x-2024|+|x-2022|\geq 4+0=4$
$\Rightarrow P\geq 4$
Vậy $P_{\min}=4$. Giá trị này đạt được khi $(x-2020)(2024-x)\geq 0$ và $x-2022=0$
Hay $x=2022$
Đúng 1
Bình luận (0)
Tìm GTNN của P=2x2+y2-2xy-6x+2y+2024
P=2x2+y2-2xy-6x+2y+2024
=>2P=4x2+2y2-4xy-12x+4y+4048
=(2x-y-3)2+y2-2y+1+4038
=(2x-y-3)2+(y-1)2+4038> hoặc = 4038
Dấu = xảy ra <=>2x-y-3=0 và y-1=0=>x=2;y=1=>2p=4038=>p=2019
Vậy Pmin=2019<=>x=2;y=1
Ta có:
P = 2x2 + y2 - 2xy - 6x + 2y + 2024
P = (x2 - 2xy + y2) - 2(x - y) + 1 + (x2 - 4x + 4) + 2019
P = [(x - y)2 - 2(x - y) + 1] + (x - 2)2 + 2019
P = (x - y - 1)2 + (x - 2)2 + 2019 \(\ge\)2019 \(\forall\)x;y
Dấu "=" xảy ra <=> \(\hept{\begin{cases}x-y-1=0\\x-2=0\end{cases}}\) <=> \(\hept{\begin{cases}y=x-1\\x=2\end{cases}}\) <=> \(\hept{\begin{cases}y=1\\x=2\end{cases}}\)
Vậy MinP = 2019 <=> x = 2 và y = 1
\(P=2x^2+y^2-2xy-6x+2y+2024\)
\(\Rightarrow P=\left(x^2-2xy+y^2\right)-2\left(x-y\right)+1+\left(x^2-4x+4\right)+2019\)
\(\Rightarrow P=\left[\left(x-y\right)^2-2\left(x-y\right)+1\right]+\left(x-2\right)^2+2019\)
\(\Rightarrow P=\left(x-y-1\right)^2+\left(x-2\right)^2+2019\)
Ta có:
\(\left(x-y-1\right)^2\ge0\forall x;y\inℝ\)
\(\left(x-2\right)^2\ge0\forall x\inℝ\)
\(\Rightarrow\left(x-y-1\right)^2+\left(x-2\right)^2\ge0\forall x;y\inℝ\)
\(\Rightarrow\left(x-y-1\right)^2+\left(x-2\right)^2+2019\ge2019\forall x;y\inℝ\)
\(\Rightarrow P\ge2019\forall x;y\inℝ\)
Dấu "=" xảy ra:
\(\Leftrightarrow\hept{\begin{cases}x-y-1=0\\x-2=0\end{cases}\Leftrightarrow\hept{\begin{cases}y=x-1\\x=2\end{cases}\Leftrightarrow}\hept{\begin{cases}y=1\\x=2\end{cases}}}\)
Vậy P nhỏ nhất khi P = 2019 tại x=2;y=1
Chúc bạn học tốt nhé!
bài 1 Tìm x,y sao cho biểu thức A=2x2+9y2−6xy−6x−12y+2024 đạt GTNN. Tìm giá trị đó.
A=2x^2+9y^2-6xy-6x-12y+2024
A = (x^2 -6xy +9y^2) + 4(x -3y) + x^2 - 10x + 2024
A = (x -3y)^2 +4(x -3y) + 4 + x^2 -10x +25 + 1995
A = (x -3y +2)^2 + (x -5)^2 + 1995 \geq 1995
Min A = 1995
x - 5 = 0 => x = 5
Và x - 3y + 2 = 0 hay 5 -3y +2 = 0 => -3y = -7 => y = 7/3
\(K\)\(nha!~!\)
Đúng 1
Bình luận (0)
Timf GTNN
A=2^2-20x+2024
A = 22 - 20\(x\) + 2024
A = 4 + 2024 - 20\(x\)
A = 2028 - 20\(x\)
Ta có đồ thị
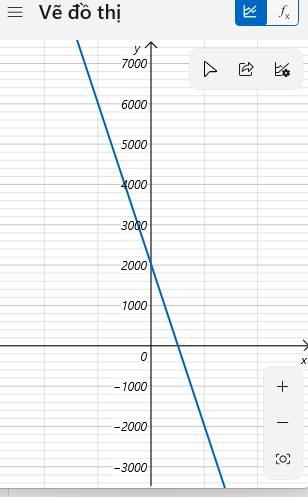
Không có giá trị nhỏ nhất em nhá
Đúng 1
Bình luận (0)

