Phan tich
a) 7x2+50x+7
b)12x2+7x-2
c)15x2+7x-2
Hệ số tự do của đa thức P ( x ) = ( 15 x 2 - 7 x - x 3 ) + ( 2 x - 12 x 2 + 7 x 3 )
A. -7
B. 1
C. 2
D. 0
Tìm x:
a) (2x-3)2+6(2x-1)=7
b) x2-7x+10=0
c) -6x2+13x-5=0
d) x4+7x2-18=0
a: Ta có: \(\left(2x-3\right)^2+6\left(2x-1\right)=7\)
\(\Leftrightarrow\left(2x-3\right)^2+6\left(2x-1\right)-7=0\)
\(\Leftrightarrow4x^2-12x+9+12x-6-7=0\)
\(\Leftrightarrow4x^2=4\)
\(\Leftrightarrow x^2=1\)
hay \(x\in\left\{1;-1\right\}\)
b: Ta có: \(x^2-7x+10=0\)
\(\Leftrightarrow\left(x-5\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=5\\x=2\end{matrix}\right.\)
Tìm x:
a) (2x-3)2+6(2x-1)=7
b) x2-7x+10=0
c) -6x2+13x-5=0
d) x4+7x2-18=0
a) \(\left(2x-3\right)^2+6\left(2x-1\right)=7\\ \Rightarrow4x^2-12x+9+12x-6-7=0\\ \Rightarrow4x^2-4=0\\ \Rightarrow x^2-1=0\\ \Rightarrow x^2=1\\ \Rightarrow\left[{}\begin{matrix}x=-1\\x=1\end{matrix}\right.\)
b) \(x^2-7x+10=0\\ \Rightarrow\left(x^2-2x\right)-\left(5x-10\right)=0\\ \Rightarrow\left(x-2\right)\left(x-5\right)=0\\ \Rightarrow\left[{}\begin{matrix}x-2=0\\x-5=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=2\\x=5\end{matrix}\right.\)
c) \(-6x^2+13x-5=0\\ \Rightarrow-\left(6x^2-13x+5\right)=0\\ \Rightarrow-\left[\left(6x^2-10x\right)-\left(3x-5\right)\right]=0\\ \Rightarrow-\left[2x\left(3x-5\right)-\left(3x-5\right)\right]=0\\ \Rightarrow-\left(2x-1\right)\left(3x-5\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}-\left(2x-1\right)=0\\3x-5=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}2x-1=0\\3x-5=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=\dfrac{5}{3}\end{matrix}\right.\)
d) \(x^4+7x^2-18=0\\ \Rightarrow\left(x^4-4\right)+\left(7x^2-14\right)=0\\ \Rightarrow\left(x^2-2\right)\left(x^2+2\right)+7\left(x^2-2\right)=0\\ \Rightarrow\left(x^2-2\right)\left(x^2+9\right)=0\\ \Rightarrow\left[{}\begin{matrix}x^2-2=0\\x^2+9=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=\pm\sqrt{2}\\x^2=-9\left(loại\right)\end{matrix}\right.\)
Không giải phương trình, hãy xác định các hệ số a, b, c, tính biệt thức Δ và xác định số nghiệm của mỗi phương trình sau:
7 x 2 − 2 x + 3 = 0 b ) 5 x 2 + 2 10 x + 2 = 0 c ) 1 2 x 2 + 7 x + 2 3 = 0 d ) 1 , 7 x 2 − 1 , 2 x − 2 , 1 = 0
a) Phương trình bậc hai: 7 x 2 – 2 x + 3 = 0
Có: a = 7; b = -2; c = 3; Δ = b 2 – 4 a c = ( - 2 ) 2 – 4 . 7 . 3 = - 80 < 0
Vậy phương trình vô nghiệm.
b) Phương trình bậc hai 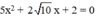
Có: a = 5; b = 2√10; c = 2; Δ = b 2 – 4 a c = ( 2 √ 10 ) 2 – 4 . 2 . 5 = 0
Vậy phương trình có nghiệm kép.
c) Phương trình bậc hai 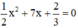
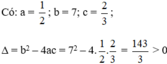
Vậy phương trình có hai nghiệm phân biệt.
d) Phương trình bậc hai 1 , 7 x 2 – 1 , 2 x – 2 , 1 = 0
Có: a = 1,7; b = -1,2; c = -2,1;
Δ = b 2 – 4 a c = ( - 1 , 2 ) 2 – 4 . 1 , 7 . ( - 2 , 1 ) = 15 , 72 > 0
Vậy phương trình có hai nghiệm phân biệt.
Kiến thức áp dụng
Phương trình ax2 + bx + c = 0 (a ≠ 0) có biệt thức Δ = b2 – 4ac.
+ Nếu Δ > 0, phương trình có hai nghiệm phân biệt 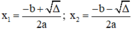
+ Nếu Δ = 0, phương trình có nghiệm kép 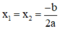 ;
;
+ Nếu Δ < 0, phương trình vô nghiệm.
Tìm đa thức M biết:
$M-5x^2-8x^2=7x^2-7x^5$M−5x2−8x2=7x2−7x5
$M=$M=
2x^2 + x - 6
7x^2 + 50x +7
12x^2 + 7x - 12
15x^2 + 7x - 2
a^2 - 5a - 14
4p^2 - 36p + 56
2x^2 + 5x +2
2x^2 + x - 6
= 2x^2 + 4x - 3x - 6
= 2x(x + 2) - 3(x + 2)
= (2x - 3)(x + 2)
7x^2 + 50x + 7
= 7x^2 + x + 49x + 7
= 7x(x + 7) + x + 7
= (7x + 1)(x + 7)
12x^2 + 7x - 12
15x^2 + 7x - 2
= 15x^2 - 3x + 10x - 2
= 3x(5x - 1) + 2(5x - 1)
= (3x + 2)(5x - 1)
a^2 - 5a - 14
= a^2 + 2a - 7a - 14
= a(a + 2) - 7(a + 2)
= (a - 7)(a + 2)
2x^2 + 5x + 2
= 2x^2 + x + 4x + 2
= 2x(x + 2) + x + 2
= (2x + 1)(x + 2)
\(2x^2+x-6=2x^2+4x-3x-6\)
\(=2x\left(x+2\right)-3\left(x+2\right)\)
\(=\left(x+2\right)\left(2x-3\right)\)
\(7x^2+50x+7\)
\(=7x^2+x+49x+7\)
\(=x\left(7x+1\right)+7\left(7x+1\right)\)
\(=\left(7x+1\right)\left(x+7\right)\)
\(12x^2+7x-12\)
\(=12x^2+16x-9x-12\)
\(=4x\left(3x+4\right)-3\left(3x+4\right)\)
\(=\left(3x+4\right)\left(4x-3\right)\)
\(4p^2-36p+56\)
\(=4p^2+8p+28p+56\)
\(=4p\left(p+2\right)+28\left(p+2\right)\)
\(=\left(p+2\right)\left(4p+28\right)\)
Tìm x:
1. ( 4x4 + 3x3 ) : ( -x3) + ( 15x2 + 6x ) : 3x = 0
2. ( 25x2 - 10x) : ( -5x) - 3( x-2) = 4
3. ( 42x3 - 12x ) : ( -6x) + 7x ( x+2) = 8
`1)<=> -4x-3 + 5x+ 2 =0`
`<=> 5x-4x = -2+3`
`<=> x =1`
`2)<=> -5x +2-3x+6 =4`
`<=> -5x-3x = 4-6-2`
`<=> -8x=-4`
`<=> x=1/2`
`3) <=> -7x^2 +2 +7x^2 +14x =8`
`<=> 14x +2 =8`
`<=> 14x = 6`
`<=> x=3/7`
tìm các nghiệm hữu tỉ của phương trình
\(a)7x^2+50x+7 \)
\(b)12x^2+7x-12=0\)
Phân tích thành nhân tử:
\(7x^2+50x+7\)