Cho tam giác ABC cân tại A,các đường phân giác BE,CF
a,cmBFEC là hình thang cân
b,cmBF=FE=EC
LL
Những câu hỏi liên quan
Cho tam giác ABC cân tại A , các phân giác BE , CF :
a) Chứng minh BFEC là hình thang cân
b) Chứng minh BF = FE = EC
Cho tam giác ABC cân tại A.Vẽ đường phân giác BE và CF
A,Chứng minh tam giác ABE=tam giác ACF
B,Tứ giác BCEF là hình thang cân
C,Chứng minh EF=EC
cho tam giác abc cân tại A các đường phân giác BE, CF ( E thuộc AC, F thuộc AB ) CHứng minh rằng
a )FB = EC
b) BFCE là hình thang cân có đáy nhỏ bằng cạnh bên
a)Xét tam giác AFC và tam giác AEB có :
góc A chung
AB = AC (gt)
góc B1 = góc C1 (gt)
=>tam giác AFC = tam giác AEC (g.c.g)
=>FC = EB (đcpcm)
b)Vì tam giác AFC = tam giác AEC (cmt)
=>AF=AE (hai cạnh tương ứng )
=>tam giác AFE cân tại A
=>góc AFE=180 độ - góc A : 2
mặt khác ta có : tam giác ABC cân tại A
=>góc B =180 độ - góc A : 2
=>góc B = góc AFE
góc B và góc AFE ở vị trí đồng vị
=>EF song song BC
=>FBCE là hình thang
=>FB = EC
mà góc B =góc C (gt)
=>FBCE là hình thang cân
Ta có :FE song song BC
=>góc EBC = góc FEB (SLT)
mà góc FBE = góc EBC (gt)
=>góc FBE = góc FEB
=>tam giác BFE cân tại F
=>EF=FB (hai cạnh tương ứng ) (đcpcm)
ta lại có :
FB=FC(cmt)
=>EC=FE (đcpcm)
Bn nhớ k cho mình nha!!!!!!!!
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A.Vẽ đường phân giác BE và CF
A,Chứng minh tam giác ABE=tam giác ACF
B,Tứ giác BCEF là hình thang cân
C,Chứng minh EF=EC
Tớ nói với cậu chỗ tin nhắn rồi .... nếu không hiểu thì báo tớ,,,,, tớ ns tiếp cho
Đúng 0
Bình luận (0)
1) cho hình tứ giác ABCD, có <A=<D=90 độ, AB//CD(AB>CD).Biết AB=BC=2CD.CM:
a) AB=BC
b) <ABC=<BCD
2) cho tam giác ABC cân tại A, các đường phân giác BE và EF.CM
a) BE,CF là hình thang cân
b) BE=FC=EC
bài 1 mình nghĩ là sai đề, bn xem lại nhé
bài 2/
a/ ta có BE, CF là p/g
=> CBE=FBE=1/2 ABC ; BCF=ECF=1/2 ACB
mà ABC=ACB => CBE=EBF=BCF=ECF
xét tam giác BFC và CEB có
BC chung; CBF=BCE (tam giác ABC cân) ; BCF=CBE (cmt)
=> tam giác BFC= tam giác CEB (g-c-g)
=> BF=CE mà AB=AC (tam giác cân) => AB-BC=AC-CE =>AF=AE
=> tam giác AEF cân tại A
=> AFE = 1/2 ( 180-A)
mà ABC = 1/2 (180-A) => AFE=ABC => EF//BC (2 góc nằm ở vị trí đồng vị)
=>BCEF LÀ HÌNH THANG mà CBF=BCE (tam giác ABC cân)
=> BCEF là hình thang cân
b/ có BE=FC (tam giác =nhau; cmt)
còn BE=FC=EC thì ko pải đâu bn, vô lý luôn đó
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A ( góc A < 40 độ) có BM,CN là hai đường phân giác của tam giác ABC.
a) Chứng minh BCMN là hình thang cân
b) BE,CF là hai đường cao của tam giác ABC. Chứng minh EMNF là hình thang cân.
Cho tam giác ABC cân tại A (góc A < 40 độ) có BM và CN là hai đường phân giác của tam giác ABC
a) Chminh BCMN là hình thang cân
b) BE,CF là hai đường cao của tam giác ABC,Ch.minh EMNF là hình thang cân
Cho tam giác ABC cân tại A, các đường phân giác BE, CF. Chứng minh rằng BFEC là hình thang cân có đáy nhỏ bằng cạnh bên.
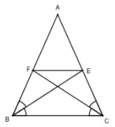
+) Do BE và CF lần lượt là tia phân giác của góc B và góc C nên ta có:
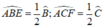
Mà tam giác ABC cân tại A nên ∠ B = ∠ C
Suy ra: ∠ ABE = ∠ ACF
Xét hai tam giác AEB và AFC
Có AB = AC ( ∆ ABC cân tại A)
∠ ABE = ∠ ACF (chứng minh trên)
∠ A là góc chung
⇒ ∆ AEB = ∆ AFC (g.c.g) ⇒ AE = AF ⇒ ∆ AEF cân tại A
⇒ ∠ AFE = ( 180 0 − ∠ A) / 2 và trong tam giác ∆ ABC: ∠ B = ( 180 0 − ∠A) / 2
⇒ ∠ AFE = ∠ B ⇒ FE//BC ( có hai góc ở vị trí đồng vị bằng nhau).
⇒ Tứ giác BFEC là hình thang.
Vì FE//BC nên ta có: ∠ FEB = ∠ EBC (so le trong)
Lại có: ∠ FBE = ∠ EBC ( vì BE là tia phân giác của góc B)
⇒ ∠ FBE = ∠ FEB
⇒ ∆ FBE cân ở F ⇒ FB = FE
⇒ Hình thang BFEC là hình thang cân có đáy nhỏ bằng cạnh bên (đpcm)
Đúng 3
Bình luận (0)
Cho tam giác ABC cân tại A (góc A<40 độ), BE, CF là 2 đường cao, BM, CN là 2 phân giác của tam giác ABC. Chứng minh BCEF và EMNF là các hình thang cân
Góc BEC=góc BFC=90 độ
=>BCEF LÀ TỨ GIÁC NỘI TIẾP
=>Góc AFE=gócC (1)
Tam giác BNC đồng dạng với tam giác BMC(g.c.g)
=>Góc BNC=góc BMC
=>BCMN là tứ giác nội tiếp
=>Góc ANM=góc AMN=góc C (2)
Từ 1 và 2
Có EF song song với MN và góc ANM=góc AMN
=>EMNF là hình thang cân