Tìm số đo các góc chưa biết của các tứ giác trong Hình 11.

Tìm số đo các góc chưa biết của các tam giác trong Hình 5.

a) Theo định lí về tổng số đo 3 góc trong tam giác ta có :
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^o}\\ \Rightarrow \widehat B = {180^o} - \widehat A - \widehat C = {180^o} - {72^o} - {44^o} = {64^o}\end{array}\)
b) Theo định lí về tổng số đo 3 góc trong tam giác ta có :
\(\begin{array}{l}\widehat D + \widehat E + \widehat F = {180^o}\\ \Rightarrow \widehat D = {180^o} - \widehat E - \widehat F = {180^o} - {59^o} - {31^o} = {90^o}\end{array}\)
c) Theo định lí về tổng số đo 3 góc trong tam giác ta có :
\(\begin{array}{l}\widehat M + \widehat N + \widehat P = {180^o}\\ \Rightarrow \widehat P = {180^o} - \widehat M - \widehat N = {180^o} - {120^o} - {33^o} = {27^o}\end{array}\)
Tìm số đo các góc chưa biết của mỗi tam giác trong Hình 7.
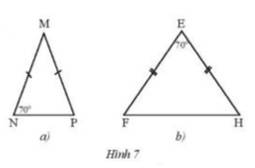
a) Vì \(\Delta MNP\) cân tại M ( theo giả thiết )
\( \Rightarrow \widehat N = \widehat P = {70^o}\) ( 2 góc đáy của tam giác cân )
\( \Rightarrow \widehat M = {180^o} - {2.70^o} = {40^o}\)
b) Xét \(\Delta EFH\) cân tại E
Theo định lí về tổng 3 góc trong tam giác ta có
\( \Rightarrow \widehat E + \widehat F + \widehat H = {180^o}\)
Mà \(\widehat F = \widehat H\)( tính chất tam giác cân )
\( \Rightarrow \widehat F = \widehat H = {180^o} - \widehat E = ({180^o} - {70^o}):2 = {55^o}\)
Tứ giác \(EFGH\) có các góc cho như trong Hình 5.
a) Chứng minh rằng \(EFGH\) là hình thang
b) Tìm góc chưa biết của tứ giác
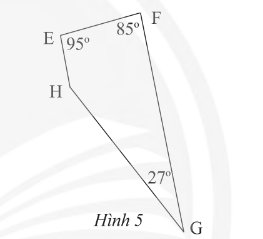
a) Ta có:
\(\widehat {\rm{E}} + \widehat {\rm{F}} = 95^\circ + 85^\circ = 180^\circ \)
Mà hai góc ở vị trí Trong cùng phía
Suy ra \(EH\;{\rm{//}}\;FG\)
Suy ra: \(EFGH\) là hình thang
b) Xét hình thang \(EFGH\) ta có: \(\widehat E + \widehat F + \widehat G + \widehat H = 360^\circ \)
\(\begin{array}{l}95^\circ + 85^\circ + 27^\circ + \widehat H = 360^\circ \\\widehat H = 153^\circ \end{array}\)
tìm số đo các góc chưa bt của tứ giác trong từng trường hợp sau:
a) tứ giác có các góc 800, 700 và 2 góc còn lại góc này gấp 2 lần góc kia
b) tứ giác có số đo góc lần lượt tỉ lệ vs 1:2:4:5
a) Gọi A = 80°
B = 70°
D = 2C
=> C+D = 360 - 70 - 80 = 210
=> 2C + C = 210°
=> 3C = 210°
=> C = 70°
=> D = 70 × 2 = 140°
b) Ta có : A = B/2=C/4 = D/5
Áp dụng tính chất dãy tỉ số bằng nhau ta có
=> A = 30°
=> B = 60°
=> C = 120°
=> D = 150°
Tìm số đo các góc chưa biết của các tam giác trong Hình 3 và cho biết tam giác nào là tam giác nhọn, tam giác nào là tam giác tù, tam giác nào là tam giác vuông.

a) Vì tổng 3 góc trong tam giác là \({180^o}\)
Nên ta có :
\(\begin{array}{l} \Rightarrow \widehat {DEC} + \widehat {DCE} + \widehat {CDE} = {180^o}\\ \Rightarrow \widehat {DCE} = {180^o} - \widehat {DEC} - \widehat {CDE}\\ \Rightarrow \widehat {DCE} = {180^o} - {58^o} - {32^o} = {90^o}\end{array}\)
b) Theo đề bài ta có :
\(\begin{array}{l} \Rightarrow \widehat {HGF} + \widehat {GHF} + \widehat {GFH} = {180^o}\\ \Rightarrow \widehat {GFH} = {180^o} - \widehat {HGF} - \widehat {GHF}\\ \Rightarrow \widehat {GFH} = {180^o} - {68^o} - {42^o} = {70^o}\end{array}\)
c) Theo đề bài ta có :
\(\begin{array}{l} \Rightarrow \widehat {IJK} + \widehat {JKI} + \widehat {JIK} = {180^o}\\ \Rightarrow \widehat {JIK} = {180^o} - \widehat {IJK} - \widehat {JKI}\\ \Rightarrow \widehat {JIK} = {180^o} - {27^o} - {56^o} = {97^o}\end{array}\)
a) Cho biết các số đo x,y,t trong mỗi hình a),b),c)
b)Ko dùng thước đo góc, cho biết tổng số đo các góc của một HCN.
c)Ko dùng thước đo góc , cho biết tổng số đo các góc trong một hình tứ giác lồi.
d)Có hay ko một tam giác mà cả 3 góc đều lớn hơn 60độ?
e)Có hay ko một tam giác mà cả 3 góc đều nhỏ hơn 60ođộ?

Tính số đo các góc và các cạnh chưa biết của tam giác DEF trong Hình 4.62.
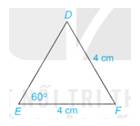
Cách 1: Vì tam giác DEF có DF=FE(=4cm) nên tam giác DEF cân tại F.
Mà \(\widehat E=60^0\)
Do đó, \(\Delta DEF \) đều. (Tam giác cân có 1 góc bằng \(60^0\))
\(\Rightarrow \widehat D = \widehat F=\widehat E=60^0\).
Cách 2: Xét tam giác DEF có DF=FE(=4cm) nên tam giác DEF cân tại F.
Suy ra \(\widehat E = \widehat D = {60^o}\) ( tính chất tam giác cân)
Áp dụng định lí tổng ba góc trong tam giác vào tam giác DEF, ta có:
\(\begin{array}{l}\widehat D + \widehat E + \widehat F = {180^o}\\ \Rightarrow {60^o} + {60^o} + \widehat F = {180^o}\\ \Rightarrow \widehat F = {60^o}\end{array}\)
Câu 9: Tổng số đo bốn góc của một ngũ giác bằng:
A. 5400 B. 1800 C. 2700 D. 3600
Câu 10: Số đo mỗi góc của tứ giác đều là:
A. 900 B. 1800 C. 2700 D. 3600
Câu 11: Đa giác có tổng số đo các góc trong bằng tổng số đo các góc ngoài là:
A. Tứ giác B. Ngũ giác C. Lục giác D. Thất giác
Câu 12: Diện tích của tam giác vuông có hai cạnh góc vuông là 4cm và 6 cm sẽ là :
A. 24cm2 B. 12cm2 C. 12cm D. 24 cm
Câu 13: Nếu một hình chữ nhật có chu vi là 22 cm và diện tích là 18 cm2
thì độ dài hai cạnh là:
A. 3 cm và 6cm B.4 cm và 5 cm C. 2 cm và 9 cm D. Đáp án khác
Câu 9: A
Câu 10: A
Câu 11: A
Câu 12: B
Câu 13: C
Bài 10. Cho tứ giác , biết . Tính các góc của tứ giác .
Bài 11. Cho tứ giác , biết . Tính các góc của tứ giác
.
Bài 12. Cho tứ giác có . Tính góc
Bài 13. Cho tứ giác biết + = 2000, + = 1800; + = 1200. Tính số đo các góc
EFGH G E 10 , F E 30 , H 2G o o EFGH
MNPQ P Q 5 , M Q 45 , N 2Q 40 o o o
MNPQ
ABCD A 70 , B 80 , C D 20 o o o C, D.
ABCD B C B D C D
tor.com
Bài 14:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{\widehat{A}}{1}=\dfrac{\widehat{B}}{3}=\dfrac{\widehat{E}}{4}=\dfrac{\widehat{F}}{7}=\dfrac{360^0}{15}=24^0\)
Do đó: \(\widehat{A}=24^0;\widehat{B}=72^0;\widehat{C}=96^0;\widehat{F}=168^0\)