Gọi O là trung điểm của AB

AC+CO=AO

DB+DO=BO

mà AO=BO và AC=BD

nên DO=CO

=>O là trung điểm của CD

=>AB và CD có cùng trung điểm

ủng hộ mk nha mọi người

Bạn tự vẽ hình nha

Câu a

Chứng minh : Kẻ OC cắt BD tại E

Xét ΔCAO và ΔEBO có :

ˆA=^OBE (=1v)

AO=BO (gt)

^COA=^BOE (đối đỉnh)

⇒ΔCAO=ΔEBO (cgv - gn )

⇒OC=OE ( hai cạnh tương ứng )

và AC=BE ( hai cạnh tương ứng )

Xét ΔOCD và ΔOED có :

OC=OE (c/m trên )

^COD=^DOE ( = 1v )

OD chung

⇒ΔOCD=ΔOED (cgv - cgv )

⇒CD=DE (hai cạnh tương ứng )

mà DE = BD + BE

và AC = BE ( c/m trên )

⇒CD=AC+BD

bạn có đọc nội quy không bạn Nguyễn Minh Huy, k k linh tinh nhé, (dcmm)

ai chơi ngọc rồng onlie ko cho mk xin 1 nick

a) Vẽ tia CO cắt tia đối của tia By tại E

Xét tam giác vuông AOC và tam giác vuông BOE có : 

AO = OB ( gt ) 

AOC = BOE ( 2 góc đối đỉnh ) 

\(\implies\)  tam giác vuông AOC = tam giác vuông BOE ( cạnh huyền - góc nhọn ) 

\(\implies\) AC = BE ( 2 cạnh tương ứng ) 

Xét tam giác vuông DOC và tam giác vuông DOE có : 

OD chung 

OC = OE ( tam giác vuông AOC = tam giác vuông BOE ) 

\(\implies\) tam giác vuông DOC = tam giác vuông DOE ( 2 cạnh góc vuông ) 

\(\implies\) CD = ED ( 2 cạnh tương ứng ) 

Mà ED = EB + BD 

\(\implies\) ED = AC + BD 

\(\implies\) CD = AC + BD 

b) Xét tam giác DOE vuông tại O có : 

OE² + OD² = DE² ( Theo định lý Py - ta - go ) 

 Xét tam giác BOE vuông tại B có : 

OB² + BE² = OE² ( Theo định lý Py - ta - go ) ( * ) 

 Xét tam giác BOD vuông tại B có : 

OB² + BD² = OD² ( Theo định lý Py - ta - go ) ( ** )

Cộng ( * ) với ( ** ) vế với vế ta được : 

OE² + OD² = 2. OB² + EB² + DB² 

Mà OE² + OD² = DE² ( cmt ) 

\(\implies\) DE² = 2. OB² + EB² + DB² 

                 = 2. OB² + EB . ( DE - BD ) + DB . ( DE - BE ) 

                 = 2. OB² + EB . DE - EB . BD + DB . DE - DB . BE 

                 = 2. OB² + ( EB . DE + DB . DE ) - 2 . BD . BE 

                 = 2. OB² + DE . ( EB + DB ) - 2 . BD . BE  

                 = 2. OB² + DE² - 2 . BD . BE  

\(\implies\) 2. OB² - 2 . BD . BE = 0 

\(\implies\) 2. OB² = 2 . BD . BE

\(\implies\) OB² = BD . BE 

Mà BE = AC ( cmt ) ; OB = AB / 2 ( gt ) 

\(\implies\) AC . BD = ( AB / 2 )² 

\(\implies\) AC . BD = AB² / 4 

a) Vẽ tia CO cắt tia đối của tia By tại E

Xét tam giác vuông AOC và tam giác vuông BOE có : 

AO = OB ( gt ) 

AOC = BOE ( 2 góc đối đỉnh ) 

⇒  tam giác vuông AOC = tam giác vuông BOE ( cạnh huyền - góc nhọn ) 

⇒ AC = BE ( 2 cạnh tương ứng ) 

Xét tam giác vuông DOC và tam giác vuông DOE có : 

OD chung 

OC = OE ( tam giác vuông AOC = tam giác vuông BOE ) 

⇒ tam giác vuông DOC = tam giác vuông DOE ( 2 cạnh góc vuông ) 

⇒ CD = ED ( 2 cạnh tương ứng ) 

Mà ED = EB + BD 

⇒ ED = AC + BD 

⇒ CD = AC + BD 

b) Xét tam giác DOE vuông tại O có : 

OE² + OD² = DE² ( Theo định lý Py - ta - go ) 

 Xét tam giác BOE vuông tại B có : 

OB² + BE² = OE² ( Theo định lý Py - ta - go ) ( * ) 

 Xét tam giác BOD vuông tại B có : 

OB² + BD² = OD² ( Theo định lý Py - ta - go ) ( ** )

Cộng ( * ) với ( ** ) vế với vế ta được : 

OE² + OD² = 2. OB² + EB² + DB² 

Mà OE² + OD² = DE² ( cmt ) 

⇒ DE² = 2. OB² + EB² + DB² 

                 = 2. OB² + EB . ( DE - BD ) + DB . ( DE - BE ) 

                 = 2. OB² + EB . DE - EB . BD + DB . DE - DB . BE 

                 = 2. OB² + ( EB . DE + DB . DE ) - 2 . BD . BE 

                 = 2. OB² + DE . ( EB + DB ) - 2 . BD . BE  

                 = 2. OB² + DE² - 2 . BD . BE  

⇒ 2. OB² - 2 . BD . BE = 0 

⇒ 2. OB² = 2 . BD . BE

⇒ OB² = BD . BE 

Mà BE = AC ( cmt ) ; OB = AB / 2 ( gt ) 

⇒ AC . BD = ( AB / 2 )² 

⇒ AC . BD = AB² / 4 

AC<AM

=>C nằm giữa A và M

=>MC=AM-AC=1cm

BD<BM

=>D nằm giữa B và M

=>BD+DM=BM

=>DM=1cm=MC

=>M là trung điểm của CD

a) Trên tia ab, điểm C nằm giữa 2 điểm A và B vì AC<AB (AC=3cm, AB=6cm)
b) Vì C nằm giữa A,B nên AC+CB=AB (AC=3cm, AB=6cm)
                           3+CB=6
                               CB=6-3
                               CB=3
                           =>CB=3cm
c) C là trung điểm của AB vì:
        - C nằm giữa A,B (câu a)
        - C cách đều A,B \(AC=CB=\frac{AB}{2}=\frac{6}{2}=3\)
d) Trên tia ab, điểm B nằm giữa C,D vì hai tia đối nhau BC,BD đều chung gốc B và trên cùng đường thẳng
    Vì B nằm giữa C,D nên CB + BD= CD (CB=3cm, BD=2cm)
                          3+2=CD
                          3+2=5
                      =>CD=5cm

^{bằng 5 dấy bạn ạ} 

a: Kẻ CO cắt BD tại E

Xét ΔOAC vuông tại A và ΔOBE vuông tại B có

OA=OB

góc COA=góc EOB

Do đó: ΔOAC=ΔOBE

=>OC=OE

Xét ΔDCE có

DO vừa là đường cao, vừalà trung tuyến

nên ΔDEC cân tại D

=>góc DCE=góc DEC=góc CAO

=>CO là phân giác của góc DCA

Kẻ CH vuông góc với CD

Xét ΔCAO vuông tại A và ΔCHO vuông tại H có

CO chung

góc ACO=góc HCO

DO đó: ΔCAO=ΔCHO

=>OA=OH=OB và CH=CA

Xét ΔOHD vuông tại H và ΔOBD vuông tại B có

OD chung

OH=OB

Do đó: ΔOHD=ΔOBD

=>DH=DB

=>AC+BD=CD
b: AC*BD=CH*HD=OH^2=R^2=AB^2/4

=>4*AC*BD=AB^2

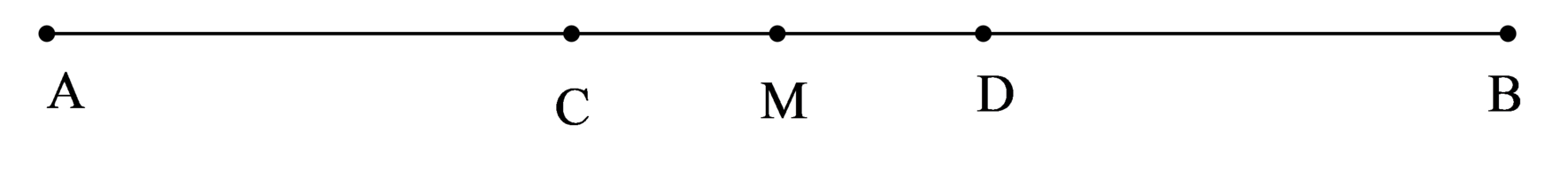
a) Điểm D nằm giữa A, B nên AD + BD = AB

AD + 3 = 8 nên AD = 5cm

C và D cùng thuộc tia AB mà AC = 3cm, AD = 5cm; nên AC < AD hay C nằm giữa A và D ta có:

AC + CD = AD

3 + CD = 5 nên CD = 2cm

b) M là trung điểm của AB nên AM = AB 2 = 8 2 = 4 cm  

Trên tia AB có AC < AM (vì 3 < 4) nên C nằm giữa A và M nên:

AC + CM = AM

3 + CM = 4 hay CM = 1cm

Trên tia AB có AM < AD ( vì 4 < 5) nên M nằm giữa A và D nên:

AM + MD = AD

4 + MD = 5 hay MD = 1cm

Ta có M nằm giữa C và D. Vì MC + MD = CM ( 1 + 1 =2) đồng thời CM = MD nên M là trung điểm của đoạn CD.