mik xin sua lai cho nay

a*990+b*99+c*10+d=bcd*2

a*990+b*99+c*10+d=(b*100+c*10+d)*2

a*990+b*99+c*10+d=b*200+c+20+d

a*990=b*101

Ban cu the ma lam nha

abcd -bcd*2 = ac

(a*1000+b*100+c*10+d) - bcd*2 = a*10+b

a*1000+b*100+c*10+d=a*10+b+bcd*2

a*990+b*99+c*10+d=bcd*2

a*990+b*99+c*10+d=b*100+c*10+d

      a*990=b

Mik nghi chi duoc vay thui hihi

Từ:   abcd - bcd x 2 = ac (a khác 0, a,b,c < 10) ta có : a000 – bcd = ac

Ta đặt phép tính như sau :
   a000

-    bcd

       ac

Ta thấy hiệu là số có 2 chữ số nên a chỉ có thể là 1.

Do nhớ 1 ở hàng đơn vị sang c để được hàng chục của hiệu a bằng 1 thì c=8

Hàng đơn vị của hiệu là 8 nên d=2. Chỉ  khi b=9

Vậy số cần tìm là:  1982

số đó là:1982

Tham khảo:

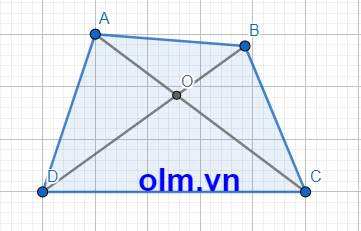
 a,  Xét \(\Delta\) AOB có: AO+OB > AB (trong tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)

Tương tự ta có:  OC + OD > DC

                           OA + OD > AD

                           OB + OC > BC 

Cộng vế với vế ta có:

OA+OB+OC+OD+OA+OD+OB+OC > AB +DC+AD+BC

(OA+OC)\(\times\)2 + (OB + OD)\(\times\)2 >  P_ABCD

AC \(\times\) 2 + BD \(\times\) 2 > P_ABCD

AC + BD > \(\dfrac{P_{ABCD}}{2}\) (đpcm)

b, Xét \(\Delta\) ABD có: AB + AD > BD (trong tam giác tổng hai cạnh bao giờ cũng lớn hơn cạnh còn lại)

Tương tự ta có:   AD + DC > AC 

                            DC + CB > DB 

                            CB + AB > AC 

  Cộng vế với vế ta có: 

AB+AD+AD+DC+DC+CB+CB+AB >BD+ AC+DB+AC

2AB+2BC+2CD+2AD> 2AC + 2BD 

2(AB + BC + CD + AD) > 2(AC + BD)

    AB + BC + CD + AD > AC + BD

       P_ABCD > AC + BD (đpcm)

Hi vọng bạn có kiến thức vững về BĐT tam giác nha, mấy bài này toàn BĐT tam giác thoi, mình ko chứng minh lại đâu.

Bài 3:

a) Xét tam giác AOB: \(OB>AB-AO\)

Xét tam giác DOC: \(OD>DC-OC\)

Cộng vế theo vế: \(OB+OD>AB+DC-\left(AO+OC\right)\Leftrightarrow BD>AB+DC-AC\Leftrightarrow BD+AC>AB+DC\)

b) Hoàn toàn tương tự với 2 tam giác AOD và BOC:

\(\Rightarrow\hept{\begin{cases}OD>AD-AO\\OB>BC-OC\end{cases}\Rightarrow BD>AD+BC-AC\Leftrightarrow BD+AC>AD+BC}\)

Bài 4: 

a) Từ câu 3 ta có \(\hept{\begin{cases}BD+AC>AB+CD\\BD+AC>AD+BC\end{cases}}\)Cộng vế theo vế:

\(\Rightarrow2\left(BD+AC\right)>AB+BC+CD+DA=P_{ABCD}\Rightarrow BD+AC>\frac{P_{ABCD}}{2}\)

b) Câu này thực ra không cần đề cho trước \(AC< \frac{P_{ABCD}}{2}\)đâu, vì đây là điều hiển nhiên mà

Xét 2 tam giác ABC và ADC: \(\hept{\begin{cases}AC< AB+BC\\AC< AD+DC\end{cases}}\)cộng vế theo vế:

\(\Rightarrow2AC< AB+BC+CD+DA=P_{ABCD}\Rightarrow AC< \frac{P_{ABCD}}{2}\)(1)

Hoàn toàn tương tự với 2 tam giác ABD và CBD \(\Rightarrow BD< \frac{P_{ABCD}}{2}\)(2)

Cộng (1) và (2) vế theo vế: \(AC+BD< P_{ABCD}\)

Chọn D

Do hình thang ABCD có 2 đường chéo vuông góc với nhau nên 

S_ABCD= 1/2 . AC . BD = 1/2 . 6 . 3,6 = 10,8 ( dm² )

Vậy S_ABCD = 10,8dm²

Hok tốt

Do hình thang ABCD có 2 đường chéo vuông góc với nhau nên 

S_ABCD= 1/2.AC.BD=1/2.6.3,6=10,8(dm²)

Vậy S_ABCD=10,8dm²

cảm ơn