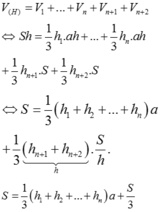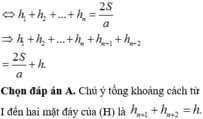Tìm hình lăng trụ có thể lấy một mặt bất kì làm mặt đáy.
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
H24
Những câu hỏi liên quan
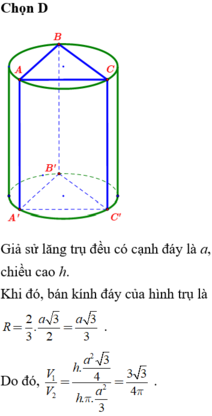
Cho hình lăng trụ đều và một hình trụ có hai đáy là hai hình tròn ngoại tiếp hai mặt đáy của hình lăng trụ. Gọi
V
1
,
V
2
lần lượt là thể tích khối lăng trụ và khối trụ. Tính
V
1
V
2
Đọc tiếp
Cho hình lăng trụ đều và một hình trụ có hai đáy là hai hình tròn ngoại tiếp hai mặt đáy của hình lăng trụ. Gọi V 1 , V 2 lần lượt là thể tích khối lăng trụ và khối trụ. Tính V 1 V 2
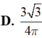
Khẳng đỉnh nào sau đây là sai?
A. Có một mặt cầu đi qua các đỉnh của một tứ diện bất kì.
B. Có một mặt cầu đi qua các đỉnh của một hình lăng trụ có đáy là một tứ giác lồi.
C. Có một mặt cầu đi qua các đỉnh của một hình hộp chữ nhật.
D. Có một mặt cầu đi qua các đỉnh của một hình chóp đều.
Chọn B.
Nếu có một mặt cầu ngoại tiếp lăng trụ thì đáy của lăng trụ phải nội tiếp trong một đường tròn, điều này không đúng cho tứ giác lồi bất kì.
Đúng 0
Bình luận (0)
a) Cho hình lăng trụ ABCDE.ABCDE có cạnh bên AA vuông góc với một mặt phẳng đáy (Hình 18a). Có nhận xét gì về các mặt bên của hình lăng trụ này?b) Cho hình lăng trụ có đáy là đa giác đều và có cạnh bên vuông góc với một mặt phẳng đáy (Hình 18b). Có nhận xét gì các mặt bên của hình lăng trụ này?c) Một hình lăng trụ nếu có đây là hình bình hành và có cạnh bên vuông góc với mặt phẳng đáy (Hình 18c) thì có bao nhiêu mặt là hình chữ nhật?d) Một hình hộp nếu có đáy là hình chữ nhật và có cạnh bên vuôn...
Đọc tiếp
a) Cho hình lăng trụ \(ABCDE.A'B'C'D'E'\) có cạnh bên \(AA'\) vuông góc với một mặt phẳng đáy (Hình 18a). Có nhận xét gì về các mặt bên của hình lăng trụ này?
b) Cho hình lăng trụ có đáy là đa giác đều và có cạnh bên vuông góc với một mặt phẳng đáy (Hình 18b). Có nhận xét gì các mặt bên của hình lăng trụ này?
c) Một hình lăng trụ nếu có đây là hình bình hành và có cạnh bên vuông góc với mặt phẳng đáy (Hình 18c) thì có bao nhiêu mặt là hình chữ nhật?
d) Một hình hộp nếu có đáy là hình chữ nhật và có cạnh bên vuông góc với mặt phẳng đáy (Hinh 18d) thì có bao nhiêu mặt là hình chữ nhật?
a: Các mặt bên của hình lăng trụ này vừa là hình chữ nhật, vừa vuông góc với đáy
b: Các mặt bên của hình lăng trụ này vừa là hình chữ nhật, vừa vuông góc với đáy
c: Có 4 mặt bên là hình chữ nhật
d: Có tất cả là 6 mặt là hình chữ nhật
Đúng 0
Bình luận (0)
Hãy cho biết :
a) Một lăng trụ đứng có 6 mặt thì đáy của lăng trụ đó là hình gì ?
b) Một lăng trụ đứng có 8 mặt thì đáy của lăng trụ đó là hình gì ?
a: Hình tứ giác
b: Hình lục giác
Đúng 0
Bình luận (0)
Quan sát các hình lăng trụ đứng trên hình vẽ rồi điền số thích hợp vào các ô trống ở bảng sau:
Hình lăng trụ
Số cạnh của một đáy (n)
Số mặt (m)
Số đỉnh (d)
Số cạnh (c)
a)
b)
Có thể tìm được một lăng trụ đứng có 15 đỉnh hay không?
Đọc tiếp
Quan sát các hình lăng trụ đứng trên hình vẽ rồi điền số thích hợp vào các ô trống ở bảng sau:
| Hình lăng trụ | Số cạnh của một đáy (n) | Số mặt (m) | Số đỉnh (d) | Số cạnh (c) |
| a) | ||||
| b) |
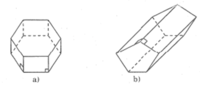
Có thể tìm được một lăng trụ đứng có 15 đỉnh hay không?
| Hình lăng trụ | Số cạnh của một đáy (n) | Số mặt (m) | Số đỉnh (d) | Số cạnh (c) |
| a) | 6 | 8 | 12 | 18 |
| b) | 5 | 7 | 10 | 15 |
Không thể làm một hình lăng trụ đứng có 15 đỉnh vì d = 2n (số đỉnh của hình lăng trụ là một số chẵn)
Đúng 0
Bình luận (0)
Cho hình lăng trụ đều có độ dài cạnh đáy bằng a. Chiều cao của hình lăng trụ bằng h, diện tích một mặt đáy bằng S. Tổng khoảng cách từ một điểm trong của hình lăng trụ đến tất cả các mặt của hình lăng trụ bằng A.
h
+
2
S
a
B.
h
+
3
S
a
C....
Đọc tiếp
Cho hình lăng trụ đều có độ dài cạnh đáy bằng a. Chiều cao của hình lăng trụ bằng h, diện tích một mặt đáy bằng S. Tổng khoảng cách từ một điểm trong của hình lăng trụ đến tất cả các mặt của hình lăng trụ bằng
A. h + 2 S a
B. h + 3 S a
C. 2 S a
D. 3 S a
Cho hình lăng trụ đều có độ dài cạnh đáy bằng a. Chiều cao của hình lăng trụ bằng h, diện tích một mặt đáy bằng S. Tổng khoảng cách từ một điểm trong của hình lăng trụ đến tất cả các mặt của hình lăng trụ bằng
Đọc tiếp
Cho hình lăng trụ đều có độ dài cạnh đáy bằng a. Chiều cao của hình lăng trụ bằng h, diện tích một mặt đáy bằng S. Tổng khoảng cách từ một điểm trong của hình lăng trụ đến tất cả các mặt của hình lăng trụ bằng
![]()
![]()
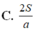
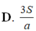
Chọn A
Xét hình lăng trụ đều (H) đã cho có đáy là đa giác đều n đỉnh. Xét điểm trong I của hình lăng trụ đều (H) đã cho. Khi đó nối I với các đỉnh của (H) ta được n+2 khối chóp có đỉnh là I, trong đó có hai khối chóp có đỉnh là I và mặt đáy là mặt đáy của (H); và n khối chóp có đỉnh I và mặt đáy là mặt bên của (H). Diện tích mỗi mặt
đáy của (H) bằng S; diện tích mỗi mặt bên của (H) bằng ah. Gọi h1, h2, .., hn, hn+1, hn2 lần lượt là khoảng cách từ I đến các mặt bên của (H) và các mặt đáy của (H). Vậy theo công thức tính thể tích của khối lăng trụ và khối chóp ta có:
![]()
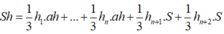
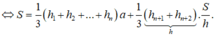
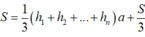
![]()
Chú ý tổng khoảng cách từ I đến hai mặt đáy của (H) là ![]()
Đúng 0
Bình luận (0)
Một hình lăng trụ có đáy là tam giác đều cạnh a, cạnh bên bằng b và tạo với mặt phẳng đáy một góc α. Thể tích của lăng trụ đó là A.
3
a
2
bsinα
12
B.
3
a
2
bcosα
12...
Đọc tiếp
Một hình lăng trụ có đáy là tam giác đều cạnh a, cạnh bên bằng b và tạo với mặt phẳng đáy một góc α. Thể tích của lăng trụ đó là
A. 3 a 2 bsinα 12
B. 3 a 2 bcosα 12
C. 3 a 2 bcosα 4
D. 3 a 2 bsinα 4
Một hình lăng trụ có đáy là tam giác đều cạnh a, cạnh bên bằng b và tạo với mặt phẳng đáy một góc α. Thể tích của lăng trụ đó là A.
3
a
2
b
sin
α
12
B.
3
a
2
b
cos
α...
Đọc tiếp
Một hình lăng trụ có đáy là tam giác đều cạnh a, cạnh bên bằng b và tạo với mặt phẳng đáy một góc α. Thể tích của lăng trụ đó là
A. 3 a 2 b sin α 12
B. 3 a 2 b cos α 4
C. 3 a 2 b sin α 4
D. 3 a 2 b cos α 12