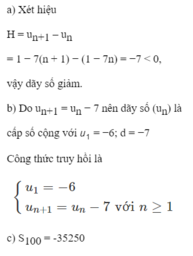Chứng minh dãy số hữu hạn sau là cấp số cộng: \(1; - 3; - 7; - 11; - 15\).
H24
Những câu hỏi liên quan
Chứng minh mỗi dãy số sau là cấp số cộng. Xác định công sai của mỗi cấp số cộng đó.
a) 3; 7; 11; 15; 19; 23.
b) Dãy số \(\left( {{u_n}} \right)\) với \({u_n} = 9n - 9\).
c) Dãy số \(\left( {{v_n}} \right)\) với \({v_n} = an + b\), trong đó \(a\) và \(b\) là các hằng số.
a) Dãy số: 3; 7; 11; 15; 19; 23 là cấp số cộng có công sai \(d = 4\).
b) Ta có: \({u_{n + 1}} = 9\left( {n + 1} \right) - 9 = 9n + 9 - 9 = \left( {9n - 9} \right) + 9 = {u_n} + 9\).
Vậy dãy số \(\left( {{u_n}} \right)\) là cấp số cộng có công sai \({\rm{d}} = 9\).
c) Ta có: \({v_{n + 1}} = a\left( {n + 1} \right) + b = an + a + b = \left( {an + b} \right) + a = {v_n} + a\).
Vậy dãy số \(\left( {{v_n}} \right)\) là cấp số cộng có công sai \({\rm{d}} = a\).
Đúng 0
Bình luận (0)
Cho hai cấp số cộng hữu hạn
(
a
n
)
và
(
b
n
)
đều có 100 số hạng và
a
1
4
,
a
2
7
,...,
a
100
và
b
1
1
,
b
2...
Đọc tiếp
Cho hai cấp số cộng hữu hạn ( a n ) và ( b n ) đều có 100 số hạng và a 1 = 4 , a 2 = 7 ,..., a 100 và b 1 = 1 , b 2 = 6 , . . . , b 100 . Hỏi có bao nhiêu số có mặt đồng thời trong cả hai dãy số trên ?
A. 32.
B. 20.
C. 33.
D. 53.
Cho dãy số (an) xác định bởi: a1=5; an= an-1 + 3n ∀ n ≥ 2. Chứng minh dãy số bn= an+1 - an ∀ n ≥ 2 là một cấp số cộng.
cho dãy số \(\left(u_n\right)\) được xác định như sau: \(\hept{\begin{cases}u_1=u_2=1\\u_{n+1}=\sqrt{u_n}+\sqrt{u_{n-1}},\end{cases}\left(n\ge2,n\in N\right)}\)
Chứng minh dãy \(\left(u_n\right)\)có giới hạn hữu hạn. Tính giới hạn đó.
Cho dãy số
(
u
n
)
u
1
1
;
u
2
...
Đọc tiếp
Cho dãy số ( u n ) u 1 = 1 ; u 2 = 2 u n + 1 = 2 u n - u n - 1 + 1 v ớ i n ≥ 2
a) Viết năm số hạng đầu của dãy số;
b) Lập dãy số ( v n ) với v n = u n + 1 − u n . Chứng minh dãy số (vn) là cấp số cộng;
Cho dãy số
(
u
n
)
với
u
n
1
-
7
n
a) Khảo sát tính tăng, giảm của dãy số;b) Chứng minh dãy số trên là cấp số cộng. Lập công thức truy hồi của dãy số;c) Tính tổng 100 số hạng đầu của dãy số.
Đọc tiếp
Cho dãy số ( u n ) với u n = 1 - 7 n
a) Khảo sát tính tăng, giảm của dãy số;
b) Chứng minh dãy số trên là cấp số cộng. Lập công thức truy hồi của dãy số;
c) Tính tổng 100 số hạng đầu của dãy số.
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = - 2n + 3\). Chứng minh rằng \(\left( {{u_n}} \right)\) là một cấp số cộng. Xác định số hạng đầu và công sai của cấp số cộng này.
Ta có: \({u_n} - {u_{n - 1}} = \left( { - 2n + 3} \right) - \left[ { - 2\left( {n - 1} \right) + 3} \right] = - 2,\;\forall n \ge 2\).
Vậy \({u_n} = - 2n + 3\) là một cấp số cộng với \({u_1} = 1\) và công sai \(d = - 2\).
Đúng 0
Bình luận (0)
Chứng minh , kiểm tra 1 dãy số có là cấp số cộng hay không ? xác định U1 , d
a , \(\left\{{}\begin{matrix}u_1\\u_n+1=u_n-n\end{matrix}\right.\)
b , \(\left\{{}\begin{matrix}u_1=a\\u_n+1=5\end{matrix}\right.\) tìm a để d số là cấp số cộng
Cho dãy số (\(u_n\)) xác định bởi: \(\left\{{}\begin{matrix}0< u_n< 1\\u_n\left(1-u_{n+1}\right)>\dfrac{1}{4},\forall n\ge1\end{matrix}\right.\)
Chứng minh dãy số (\(u_n\)) có giới hạn hữu hạn khi \(n\rightarrow\infty\)
\(u_n-u_{n+1}=u_n+\left(1-u_{n+1}\right)-1\ge2\sqrt{u_n\left(1-u_{n+1}\right)}-1>0\)
\(\Rightarrow u_n>u_{n+1}\Rightarrow\) dãy giảm
Dãy giảm và bị chặn dưới bởi 0 nên có giới hạn hữu hạn.
Gọi giới hạn đó là k
\(\Rightarrow k\left(1-k\right)\ge\dfrac{1}{4}\Rightarrow\left(2k-1\right)^2\le0\Rightarrow k=\dfrac{1}{2}\)
Vậy \(\lim\left(u_n\right)=\dfrac{1}{2}\)
Đúng 3
Bình luận (0)