Nêu nhận xét gì về hai mặt phẳng chứa hai mặt đối diện của hình hộp
H24
Những câu hỏi liên quan
Cho hai mặt phẳng song song (P) và (Q). Mặt phẳng (R) cắt mặt phẳng (P) theo giao tuyến a.a) Mặt phẳng (R) có cắt mặt phẳng (Q) theo giao tuyến b, hãy nêu nhận xét về vị trí tương đối giữa hai giao tuyến a và b (Hình 64)b) Trong trường hợp mặt phẳng (R) cắt mặt phẳng (Q) theo giao tuyến b, hãy nêu nhận xét về vị trí tương đối giữa hai giao tuyến a và b (Hình 64)
Đọc tiếp
Cho hai mặt phẳng song song (P) và (Q). Mặt phẳng (R) cắt mặt phẳng (P) theo giao tuyến a.
a) Mặt phẳng (R) có cắt mặt phẳng (Q) theo giao tuyến b, hãy nêu nhận xét về vị trí tương đối giữa hai giao tuyến a và b (Hình 64)
b) Trong trường hợp mặt phẳng (R) cắt mặt phẳng (Q) theo giao tuyến b, hãy nêu nhận xét về vị trí tương đối giữa hai giao tuyến a và b (Hình 64)
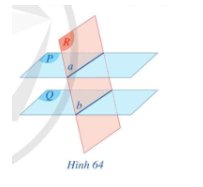
a) Do (P) // (Q) và (R) ∩ (P) = a nên (R) // (Q) hoặc (R) cắt (Q).
Giả sử (R) // (Q).
Khi đó qua đường thẳng a có hai mặt phẳng song song với (Q) là mặt phẳng (P) và (R) nên hai mặt phẳng này trùng nhau, điều này mâu thuẫn với giả thiết (R) cắt (P).
Vậy (R) cắt Q.
b) Ta có: a ⊂ (P); b ⊂ (Q) mà (P) // (Q) nên a và b không có điểm chung.
Lại có hai đường thẳng a và b cùng nằm trên mp(R)
Do đó a // b.
Đúng 0
Bình luận (0)
Trên cùng một nữa mặt phẳng có bờ chứa tia Ox vẽ hai tia Oy, Oz sao cho góc xOy 30o góc xOz 150oa Tính góc yOzb Gọi Ox là tia đối tia Ox. Viết tên các cặp góc kề bù trong hình c Kẻ Ot là tia phân giác góc yOz. Có nhận xét gì về hai góc xOy và tOz
Xem chi tiết
* Đề nên viết xuống dòng theo từng phần cho dễ hiểu. Hình tự vẽ nhé
a) Theo đề ra: Góc xOy = 30 độ
Góc xOz = 150 độ
=> Góc xOy < góc xOz => Tia Oy nằm giữa hai tia Oz và Ox
Ta có: xOy + yOz = xOz
30 độ + yOz = 150 độ
yOz = 120 độ
b) Các cặp góc kề bù là: Góc x'Oz và góc zOx
Góc x'Oy và góc yOx
c) Theo đề ra: Tia Ot là tia phân giác của góc yOz nên ta có:
=> Góc zOt = góc tOy = góc yOz : 2 = 120 độ : 2 = 60 độ
=> Góc xOy < góc tOz
=> Góc tOz = góc xOy . 2 ( 30 độ . 2 = 60 độ )
Cho hình hộp \(ABCD.A'B'C'D'\) có 6 mặt đều là hình vuông. Nêu nhận xét về góc giữa các cặp đường thẳng:
Cho hình hộp \(ABCD.A'B'C'D'\) có 6 mặt đều là hình vuông. Nêu nhận xét về góc giữa các cặp đường thẳng:
a) \(AB\) và \(BB'\);
b) \(AB\) và \(DD'\).
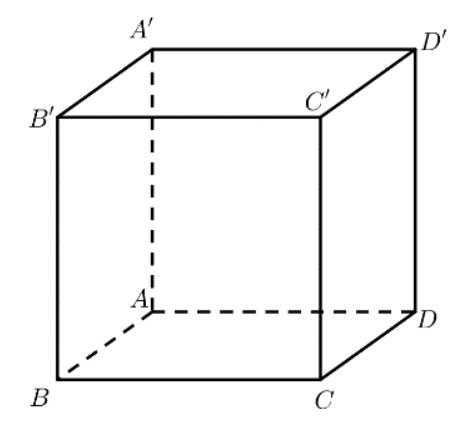
a) \(\left( {AB,BB'} \right) = \widehat {ABB'} = {90^ \circ }\).
b) Ta có: \(DD'\parallel BB' \Rightarrow \left( {AB,DD'} \right) = \left( {AB,BB'} \right) = {90^ \circ }\).
Đúng 0
Bình luận (0)
Trên cùng một nửa mặt phẳng có bờ chứa tia Ox vẽ hai tia Oy,Oz sao cho góc xOy=30 độ ; góc xOz=150 độ .
a, tính góc yOz ?
b, gọi Ox'là tia đối của Ox . Viết tên các cặp góc kề bù trong hình ?
c, Kẻ Ot là tia phân giác góc yOz . có nhận xét gì về 2 góc xOy và tOz ?
a. Trên cùng một nửa mặt phẳng bờ chứa tia Ox, tia Oy nằm giữa hai tia còn lại vì góc xOy < góc xOz (30 độ < 150 độ) nên:
xOy + yOz = xOz
30 + yOz = 150
yOz = 150 - 30
yOz = 120
Đúng 1
Bình luận (0)
Cho hình hộp ABCD.ABCD. Gọi M và N lần lượt là trung điểm của hai cạnh bên AA và CC. Một điểm P nằm trên cạnh bên DD.a) Xác định giao điểm Q của đường thẳng BB với mặt phẳng (MNP).b) Mặt phẳng (MNP) cắt hình hộp theo một thiết diện. Thiết diện đó có tính chất gì?c) Tìm giao tuyến của mặt phẳng (MNP) với mặt phẳng (ABCD) của hình hộp.
Đọc tiếp
Cho hình hộp ABCD.A'B'C'D'. Gọi M và N lần lượt là trung điểm của hai cạnh bên AA' và CC'. Một điểm P nằm trên cạnh bên DD'.
a) Xác định giao điểm Q của đường thẳng BB' với mặt phẳng (MNP).
b) Mặt phẳng (MNP) cắt hình hộp theo một thiết diện. Thiết diện đó có tính chất gì?
c) Tìm giao tuyến của mặt phẳng (MNP) với mặt phẳng (ABCD) của hình hộp.
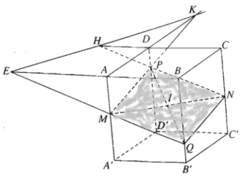
a) Ta có mặt phẳng (AA', DD') song song với mặt phẳng (BB', CC'). Mặt phẳng (MNP) cắt hai mặt phẳng nói trên theo hai giao tuyến song song.
Nếu gọi Q là điểm trên cạnh BB' sao cho NQ // PM thì Q là giao điểm của đường thẳng BB' với mặt phẳng (MNP)
Nhận xét. Ta có thể tìm điểm Q bằng cách nối P với trung điểm I của đoạn MN và đường thẳng PI cắt BB' tại Q.
b) Vì mặt phẳng (AA', BB') song song với mặt phẳng (DD', CC') nên ta có MQ // PN. Do đó mặt phẳng (MNP) cắt hình hộp theo thiết diện MNPQ là một ình bình hành.
Giả sử P không phải là trung điểm của đoạn DD'. Gọi H = PN ∩ DC , K = MP ∩ AD. Ta có D = HK là giao tuyến của mặt phẳng (MNP) với mặt phẳng (ABCD) của hình hộp.
Chú ý rằng giao điểm E = AB ∩ MQ cũng nằm trên giao tuyến d nói trên. Khi P là trung điểm của DD' mặt phẳng (MNP) song song với mặt phẳng (ABCD).
Đúng 0
Bình luận (0)
Cho hình hộp ABCD.A'B'C'D'. Gọi M và N lần lượt là trung điểm của hai cạnh bên AA' và CC'. Một điểm P nằm trên cạnh bên DD'.
a) Xác định giao điểm Q của đường thẳng BB' với mặt phẳng (MNP)
b) Mặt phẳng (MNP) cắt hình hộp theo một thiết diện. Thiết diện đó có tính chất gì ?
c) Tìm giao tuyến của mặt phẳng (MNP) với mặt phẳng (ABCD) của hình hộp
a) Ta có mặt phẳng (AA', DD') song song với mặt phẳng (BB',CC'). Mặt phẳng (MNP) cắt hai mặt phẳng nói trên theo hai giao tuyến song song.

Đúng 0
Bình luận (0)
trên cùng một nửa mặt phẳng có bờ chứa tia OX vẽ hai tia OY,OZ sao cho góc xoy = 30 độ,góc x O2 =150 độ
a,tính góc yo2
b,gọi OX là tia đối tia OX.Viết tên các cặp góc kề bù trong hình?
c, kể OT là tia phân giác ghóc YOZ.có nhận xét gì về hai góc XOY và TOZ
Trong Hình 5, xét phép chiếu theo phương l với mặt phẳng chiếu left( P right). Biết aparallel b với a subset left( Q right) và b subset left( R right). Nêu nhận xét về vị trí tương đối của hình chiếu a,b của a,b trong hai trường hợp: left( Q right)parallel left( R right);left( Q right) equiv left( R right).
Đọc tiếp
Trong Hình 5, xét phép chiếu theo phương \(l\) với mặt phẳng chiếu \(\left( P \right)\). Biết \(a\parallel b\) với \(a \subset \left( Q \right)\) và \(b \subset \left( R \right)\). Nêu nhận xét về vị trí tương đối của hình chiếu \(a',b'\) của \(a,b\) trong hai trường hợp: \(\left( Q \right)\parallel \left( R \right);\left( Q \right) \equiv \left( R \right)\).

Ta có:
\(\left. \begin{array}{l}\left( Q \right)\parallel \left( R \right)\\\left( P \right) \cap \left( Q \right) = a'\\\left( P \right) \cap \left( R \right) = b'\end{array} \right\} \Rightarrow a'\parallel b'\)
Vậy nếu \(\left( Q \right)\parallel \left( R \right)\) thì \(a'\parallel b'\); nếu \(\left( Q \right) \equiv \left( R \right)\) thì \(a' \equiv b'\).
Đúng 0
Bình luận (0)
Cho hình hộp ABCD.A’B’C’D’. Gọi N là điểm nằm trên cạnh AB, vì (α) là mặt phẳng đi qua 3 bốn điểm D, N, B’.
a) Mp(α) cắt hình hộp đã cho thiếu diện là hình gì?
b) Chứng minh rằng mặt phẳng (α) phần chia khối hộp đã cho thành hai khối đa diện H1 và H2 bằng nhau.
c) Tính tỉ số thể tích của khối đa diện H1 và thể tích tứ diện AA’BD.
Đọc tiếp
Cho hình hộp ABCD.A’B’C’D’. Gọi N là điểm nằm trên cạnh AB, vì (α) là mặt phẳng đi qua 3 bốn điểm D, N, B’.
a) Mp(α) cắt hình hộp đã cho thiếu diện là hình gì?
b) Chứng minh rằng mặt phẳng (α) phần chia khối hộp đã cho thành hai khối đa diện H1 và H2 bằng nhau.
c) Tính tỉ số thể tích của khối đa diện H1 và thể tích tứ diện AA’BD.




