phần c) ạ.Dạng bài giải pt vô tỉ bằng pp đặt ẩn phụ. p
p
HT
Những câu hỏi liên quan
giải pt (pp đặt ẩn phụ)
`(x^2 -6x)^2 +13(x-3)^2 -77=0`
Lời giải:
Đặt $(x-3)^2=a$. Khi đó pt đã cho tương đương với:
$(x^2-6x+9-9)^2+13(x-3)^2-77=0$
$\Leftrightarrow [(x-3)^2-9]^2+13(x-3)^2-77=0$
$\Leftrightarrow (a-9)^2+13a-77=0$
$\Leftrightarrow a^2-5a+4=0$
$\Leftrightarrow (a-1)(a-4)=0$
$\Leftrightarroe a=1$ hoặc $a=4$
Đến đây thì đơn giản rồi.
Đúng 4
Bình luận (0)
Giải phương trình vô tỉ sau: \(\frac{x^2}{\left(x+1-\sqrt{x+1}\right)^2}=\frac{x^2+3x+18}{\left(x+1\right)^2}\) (chú ý:làm theo pp đặt ẩn phụ)
Giải phương trình bằng pp đặt ẩn phụ:
Đọc tiếp
Giải phương trình bằng pp đặt ẩn phụ:
Giải hpt bằng pp đặt ẩn phụ
x/(x-3) + 3y/(y-1) = 5
4x/(x-3) - y/(y-1) = 7
ĐKXĐ:\(\left\{{}\begin{matrix}x\ne3\\y\ne1\end{matrix}\right.\)
Đặt `(x)/(x-3)` = a, `(y)/(y-1)` = b
\(\text{Hệ}\Leftrightarrow\left\{{}\begin{matrix}a+3b=5\\4a-b=7\end{matrix}\right.\\ \Leftrightarrow...\\ \Leftrightarrow\left\{{}\begin{matrix}a=2\\b=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{x-3}=2\\\dfrac{y}{y-1}=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=2x-6\\y=y-1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=6\\-1=0\left(vô.lí\right)\end{matrix}\right.\)
Vậy hpt vô nghiệm
Đúng 2
Bình luận (0)
giải pt sau bằng cách đặt ẩn phụ
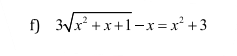
Đặt \(\sqrt{x^2+x+1}=a\)
Pt trở thành \(3a=a^2+2\)
=>(a-1)(a-2)=0
\(\Leftrightarrow\left\{{}\begin{matrix}x^2+x+1=1\\x^2+x+1=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2+x=0\\\left(x+\dfrac{1}{2}\right)^2=\dfrac{13}{4}\end{matrix}\right.\)
\(\Leftrightarrow x\in\left\{0;-1;\dfrac{\sqrt{13}-1}{2};\dfrac{-\sqrt{13}-1}{2}\right\}\)
Đúng 3
Bình luận (0)
giải các pt sau bằng cách đặt ẩn phụ
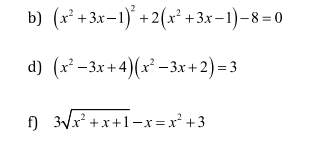
b: \(\Leftrightarrow\left(x^2+3x-1\right)^2+4\left(x^2+3x-1\right)-2\left(x^2+3x-1\right)-8=0\)
\(\Leftrightarrow\left(x^2+3x-1\right)\left(x^2+3x-1+4\right)-2\left(x^2+3x-1+4\right)=0\)
\(\Leftrightarrow x^2+3x-3=0\)
\(\Delta=3^2-4\cdot1\cdot\left(-3\right)=9+12=21>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-3-\sqrt{21}}{2}\\x_2=\dfrac{-3+\sqrt{21}}{2}\end{matrix}\right.\)
d: \(\Leftrightarrow\left(x^2-3x\right)^2+6\left(x^2-3x\right)+8=3\)
\(\Leftrightarrow\left(x^2-3x\right)^2+5\left(x^2-3x\right)+\left(x^2-3x\right)+5=0\)
\(\Leftrightarrow x^2-3x+1=0\)
\(\Delta=\left(-3\right)^2-4\cdot1\cdot1=5>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{3-\sqrt{5}}{2}\\x_2=\dfrac{3+\sqrt{5}}{2}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
giải hệ pt bằng phương pháp đặt ẩn phụ :3x-1y=5 5x=2y=28
Giải các pt sau bằng cách đặt ẩn phụ:
A. 3x6 - 10x3 + 3= 0
Đặt x3 = a
pt <=> 3a2 - 10a + 3 = 0
<=> (a - \(\dfrac{1}{3}\))(a - 3) = 0
<=> \(\left[{}\begin{matrix}a=\dfrac{1}{3}\\a=3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{\sqrt[3]{3}}\\x=\sqrt[3]{3}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
`4(x^2 +11x+30)(x^2 +22x+120)=3x^2`
giải pt bằng đặt ẩn phụ
Để giải phương trình này bằng đặt ẩn phụ, chúng ta sẽ đặt ẩn phụ là một biến mới, ví dụ như u. Sau đó, ta thực hiện phép đặt ẩn phụ bằng cách thay thế x = u - 11. Bằng cách này, ta có thể chuyển phương trình ban đầu thành một phương trình bậc nhất với ẩn phụ u.
Đúng 0
Bình luận (0)




