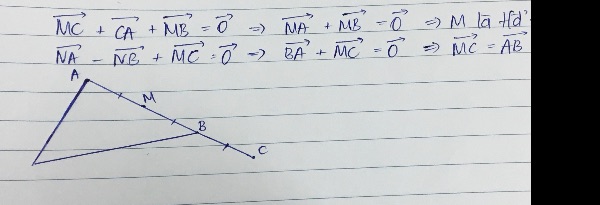Cho tam giác ABC. Xác định vị trí M thoả điều kiện MA+MB-MC=0
H24
Những câu hỏi liên quan
Cho tam giác ABC có M thỏa mãn điều kiện
M
A
→
+
M
B
→
+
M
C
→
0
→
. Xác định vị trí điểm M A. M là điểm thứ tư của hình bình hành ACBM B.M là trung điểm của đoạn thẳng AB C.M trùng...
Đọc tiếp
Cho tam giác ABC có M thỏa mãn điều kiện M A → + M B → + M C → = 0 → . Xác định vị trí điểm M
A. M là điểm thứ tư của hình bình hành ACBM
B.M là trung điểm của đoạn thẳng AB
C.M trùng C
D.M là trọng tâm tam giác ABC
Đáp án D
Gọi G là trọng tâm tam giác ABC.
Ta có ![]()
Đúng 0
Bình luận (0)
Cho tam giác ABC có M thỏa mãn điều kiện
M
A
→
+
M
B
→
+
M
C
→
0
→
Xác định vị trí điểm M A. M là điểm thứ tư của hình bình hành ACBM B.M là trung điểm của đoạn thẳng AB C.M trùng C D.M là trọng tâm ta...
Đọc tiếp
Cho tam giác ABC có M thỏa mãn điều kiện
M A → + M B → + M C → = 0 → Xác định vị trí điểm M
A. M là điểm thứ tư của hình bình hành ACBM
B.M là trung điểm của đoạn thẳng AB
C.M trùng C
D.M là trọng tâm tam giác ABC
Gọi G là trọng tâm tam giác ABC.
Ta có
![]()
Chọn D.
Đúng 0
Bình luận (0)
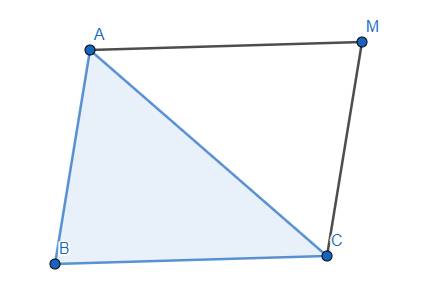
Cho tam giác ABC Xác định vị trí điểm M sao cho vecto MA - vecto MB + vecto MC = vecto 0
Ta thấy \(\overrightarrow{MA}-\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{MA}+\overrightarrow{BM}+\overrightarrow{MC}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{BA}=\overrightarrow{CM}\)
Như vậy, điểm M chính là đỉnh thứ tư của hình bình hành ABCM.
Đúng 1
Bình luận (0)
cho tam giác ABC. Hãy xác định điểm M thỏa mãn điều kiện :vecto MA -vecto Mb + vecto MC=0
Cho tam giác ABC có ba góc nhọn. Xác định vị trí của điểm M trong tam giác sao cho MA + MB + MC nhỏ nhất.
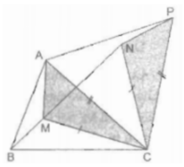
Trong ∆ ABC ta lấy điểm M. Nối MA, MB, MC.
Ta cần làm xuất hiện tổng MA + MB + MC sau đó tìm điều kiện để tổng đó nhỏ nhất.
Lấy MC làm cạnh dựng trên nửa mặt phẳng bờ BC chứa điểm A tam giác đều MCN. Suy ra: CM = MN.
Lấy AC làm cạnh dựng trên nửa mặt phẳng bờ AC không chứa điểm B tam giác đều APC. Khi đó, CA = CP
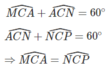
Xét ∆ AMC và ∆ PNC:
CM = CN (vì ΔMCN đều)
CA = CP (vì ΔAPC đều)
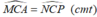
Suy ra: ∆ AMC = ∆ PNC (c.g.c)
⇒ PN = AM
MA + MB + MC = NP + MB + MN
Ta có ∆ ABC cho trước nên điểm P cố định nên BM + MN + NP ngắn nhất khi 4 điểm B, M, N, P thẳng hàng.

Đúng 0
Bình luận (0)
Cho tam giác ABC có ba góc nhọn. Xác định vị trí của điểm M trong tam giác sao cho MA + MB = MC nhỏ nhất ?
Cho tam giác ABC. Tìm tập hợp điểm M thoả mãn một trong các điều kiện saua) left|overrightarrow{MA}-overrightarrow{MB}right|left|overrightarrow{MC}right|b left|overrightarrow{MA}+overrightarrow{MB}right|0c) left|overrightarrow{MA}right|2left|overrightarrow{MC}right|d) left|overrightarrow{MB}+overrightarrow{MC}right|left|overrightarrow{MB}-overrightarrow{MC}right|
Đọc tiếp
Cho tam giác ABC. Tìm tập hợp điểm M thoả mãn một trong các điều kiện sau
a) \(\left|\overrightarrow{MA}-\overrightarrow{MB}\right|=\left|\overrightarrow{MC}\right|\)
b \(\left|\overrightarrow{MA}+\overrightarrow{MB}\right|=0\)
c) \(\left|\overrightarrow{MA}\right|=2\left|\overrightarrow{MC}\right|\)
d) \(\left|\overrightarrow{MB}+\overrightarrow{MC}\right|=\left|\overrightarrow{MB}-\overrightarrow{MC}\right|\)
Lời giải:
a.
\(|\overrightarrow{MC}|=|\overrightarrow{MA}-\overrightarrow{MB}|=|\overrightarrow{BA|}\)
Tập hợp điểm $M$ thuộc đường tròn tâm $C$ đường bán kính $AB$
b. Gọi $I$ là trung điểm $AB$. Khi đó:
\(|\overrightarrow{MA}+\overrightarrow{MB}|=|\overrightarrow{MI}+\overrightarrow{IA}+\overrightarrow{MI}+\overrightarrow{IB}|\)
\(=|2\overrightarrow{MI}+\overrightarrow{IA}+\overrightarrow{IB}|=|2\overrightarrow{MI}|=0\)
\(\Leftrightarrow |\overrightarrow{MI}|=0\Leftrightarrow M\equiv I\)
Vậy điểm $M$ là trung điểm của $AB$
Đúng 1
Bình luận (0)
c.
Trên tia đối của tia $CA$ lấy $K$ sao cho $KC=\frac{1}{3}CA$
\(|\overrightarrow{MA}|=2|\overrightarrow{MC}|\Leftrightarrow |\overrightarrow{MK}+\overrightarrow{KA}|=2|\overrightarrow{MK}+\overrightarrow{KC}|\)
\(\Leftrightarrow |\overrightarrow{MK}+4\overrightarrow{KC}|=|2\overrightarrow{MK}+2\overrightarrow{KC}|\)
\(\Leftrightarrow (\overrightarrow{MK}+4\overrightarrow{KC})^2=(2\overrightarrow{MK}+2\overrightarrow{KC})^2\)
\(\Leftrightarrow MK^2+16KC^2=4MK^2+4KC^2\)
\(\Leftrightarrow 12KC^2=3MK^2\Leftrightarrow MK=2KC=\frac{2}{3}AC\)
Vậy $M$ thuộc đường tròn tâm $K$ bán kính $\frac{2}{3}AC$
Đúng 1
Bình luận (4)
d.
Gọi $I$ là trung điểm $BC$
\(|\overrightarrow{MB}+\overrightarrow{MC}|=|\overrightarrow{MB}-\overrightarrow{MC}|\)
\(\Leftrightarrow |\overrightarrow{MI}+\overrightarrow{IB}+\overrightarrow{MI}+\overrightarrow{IC}|=|\overrightarrow{CB}|\)
\(\Leftrightarrow |2\overrightarrow{MI}|=|\overrightarrow{CB}|\Leftrightarrow |\overrightarrow{MI}|=\frac{|\overrightarrow{CB}|}{2}\)
Vậy điểm $M$ thuộc đường tròn tâm $I$ bán kính $\frac{BC}{2}$
Đúng 1
Bình luận (0)
Cho tam giác ABC a,tìm điểm M thoả mãn điều kiện vectơ MC vectơ CA vectơ MB vectơ 0 b,tìm N thoả mãn điều kiện vectơ NA vecto NB vectơ MC vectơ 0
Xem chi tiết
Cho tam giác ABC a,tìm điểm M thoả mãn điều kiện vectơ MC +vectơ CA +vectơ MB =vectơ 0 b,tìm N thoả mãn điều kiện vectơ NA- vecto NB+ vectơ MC= vectơ 0
Xem chi tiết
shsbdudjwosmgs