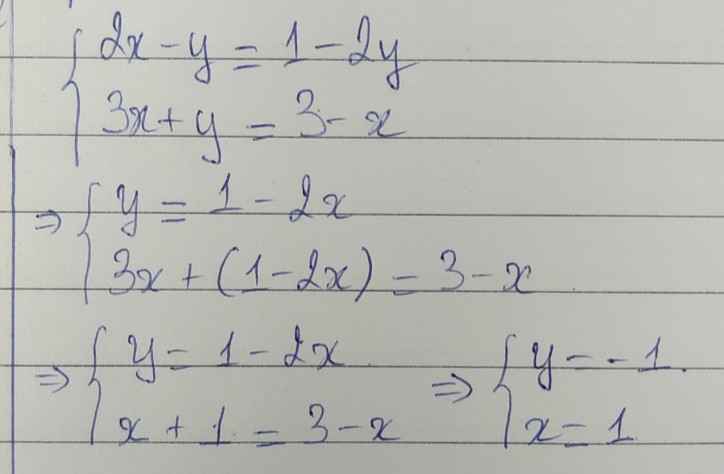\(\left(x+y\right)^3\)= 64=\(4^3\) - giải cái này như giải bậc 2 hay có gì khác không mọi người
H24
Những câu hỏi liên quan
\(16x^4-64=16\left(x^2+2\right)\left(x-\sqrt[]{2}\right)\left(x+\sqrt[]{2}\right)\)
Mọi người cho em hỏi sao đáp án ra như trên mà không phải 16(x2-2)(x2 +2) ??? Làm ơn giải giúp em ạ
16x4 - 64 = 16(x4 - 4) = 16[(x2)2 - 22] = 16(x2 - 2)(x2 + 2) = 16[x2 -\(\left(\sqrt{2}\right)^2\)](x2 + 2) = 16\(\left(x-\sqrt{2}\right)\left(x+\sqrt{2}\right)\left(x^2+2\right)\)
Đúng 0
Bình luận (0)
\(16x^4-64\)
\(=16\left(x^4-4\right)\)
\(=16\left(x^2-2\right)\left(x^2+2\right)\)
\(=16\left(x^2-\left(\sqrt{2}\right)^2\right)\left(x^2+2\right)\)
\(=16\left(x-\sqrt{2}\right)\left(x+\sqrt{2}\right)\left(x^2+2\right)\)
Bài này ra kết quả trên là lớp 9 . Còn lớp 8 là : \(16\left(x^2-2\right)\left(x^2+2\right)\)
Đúng 0
Bình luận (0)
\(16x^4-64=16\left(x^4-4\right)=16\left[\left(x^2\right)^2-2^2\right]=16\left(x^2+2\right)\left(x^2-2\right)=16\left(x^2+2\right)\left(x-\sqrt{2}\right)\left(x+\sqrt{2}\right)\)
Đúng 0
Bình luận (0)
Mọi người ơi,cái bài này nè :Tính D = 1/1.2.3 + 1/2.3.4 + 1/3.4.5 +...+ 1/18.19.20 - 3/1.2 - 3/2.3 - 3/4.5 - ...- 3/19.20 có kết quả bằng - 1977/760 phải không hay là kết quả khác,nếu khác các bạn giải cho mình nha,ai nhanh mình tick cho !!!!!!!!
D=1/2.[1/1.2-1/2.3+1/2.3-1/3.4+...+1/18.19-1/19.20]-3.[1-1/2+1/2-1/3+1/3-1/4+...+1/19-1/20]
=1/2.[1/2-1/380]-3.[1-1/20]
=1/2.[189/380]-3.[19/20]
=189/760-57/20
=189/760-2166/760
=-1977/760
Nhớ nhak
Đúng 0
Bình luận (0)
Bài này em làm mãi không ra mọi người giúp em với
Giải hệ phương trình
\(\begin{cases}\left(18x+9\right)\sqrt{x^2+x+1}=y\sqrt{4y^2+27}\\\left(2y+3\right)^2=24\sqrt{x}\left(2y-9\right)\end{cases}\)
Giải hệ phương trình : \(\hept{\begin{cases}\left(x+y\right)^4+3=4\left(x+y\right)\\\frac{x^4-y^4}{64}+\frac{9\left(x^2-y^2\right)}{32}+\frac{7\left(x-y\right)}{8}+3In\left(\frac{x-3}{y-3}\right)=0\end{cases}}\)
3In
TRONG MƠ TÔI THẤY CÓ NGƯỜI HỎI :
CĂN BẬC 2 CỦA VÔ CỰC LÀ GÌ
MỌI NGƯỜI CÓ THỂ GIÚP TÔI GIẢI BÀI TOÁN NÀY ĐƯỢC KHÔNG Ạ ĐỂ TỐI ĐẾN LẠI MƠ TIẾP NÓI KẾT QUẢ CHO NGƯỜI ĐÓ MÀ HÌNH NHƯ CÓ GÌ SAI SAI NHỈ ???
MỌI NGƯỜI CÓ THỂ GIÚP TÔI GIẢI BÀI TOÁN NÀY ĐƯỢC KHÔNG Ạ ĐỂ TỐI ĐẾN LẠI MƠ TIẾP NÓI KẾT QUẢ CHO NGƯỜI ĐÓ MÀ HÌNH NHƯ CÓ GÌ SAI SAI NHỈ ???
Vì ∞∞∞∞ rơi vào dạng không xác định, ta áp dụng quy tắc L'Hospital's. Quy tắc L'Hospital khẳng định rằng giới hạn của một thương các hàm số bằng giới hạn của thương các đạo hàm của chúng.
limn→∞n√n=limn→∞ddn[n]ddn[√n]
:))))))))))))))))
Xem thêm câu trả lời
1) giải hệ phương trình
\(\left\{{}\begin{matrix}\left(y+x\right)^2-5\left(y+x\right)-6=0\\y-x-3=0\end{matrix}\right.\)
Mọi người ơi, cố gắng giúp em với được không ạ!!!!!!!!!Em cảm on rất nhiều ạ.
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x+y+1\right)\left(x+y-6\right)=0\\y-x-3=0\left(3\right)\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x=-\left(y+1\right)\left(1\right)\\x=6-y\left(2\right)\end{matrix}\right.\\y-x-3=0\left(3\right)\end{matrix}\right.\)
\(thế\left(1\right)\left(2\right)vào\left(3\right)\Rightarrow\left(x;y\right)\)
Đúng 0
Bình luận (0)
Giải phương trình:1, left(sqrt{x+3}-sqrt{x+1}right)left(x^2+sqrt{x^2+4x+3}right)2x2, sqrt{2x+4}-2sqrt{2-x}frac{6x-4}{sqrt{x^2+4}}3, sqrt{x^2+15}3x-2+sqrt{x^2+8}- Sử dụng phương pháp liên hợpMọi người giúp mình với ạ mình đang cần gấp!À sau khi nhân liên hợp chia ra 2 trường hợp, VD như bài 3 sau khi nhân liên hợp sẽ được: left(x-1right)left(frac{x+1}{sqrt{x^2+15}+4}-3-frac{x+1}{sqrt{x^2+8}+3}right)0Nếu được mọi người giải thích giùm em tại sao biểu thức trong dấu ngoặc thứ 2 luôn luôn khác 0 ạ (...
Đọc tiếp
Giải phương trình:
1, \(\left(\sqrt{x+3}-\sqrt{x+1}\right)\left(x^2+\sqrt{x^2+4x+3}\right)=2x\)
2, \(\sqrt{2x+4}-2\sqrt{2-x}=\frac{6x-4}{\sqrt{x^2+4}}\)
3, \(\sqrt{x^2+15}=3x-2+\sqrt{x^2+8}\)
- Sử dụng phương pháp liên hợp
Mọi người giúp mình với ạ mình đang cần gấp!
À sau khi nhân liên hợp chia ra 2 trường hợp, VD như bài 3 sau khi nhân liên hợp sẽ được: \(\left(x-1\right)\left(\frac{x+1}{\sqrt{x^2+15}+4}-3-\frac{x+1}{\sqrt{x^2+8}+3}\right)=0\)
Nếu được mọi người giải thích giùm em tại sao biểu thức trong dấu ngoặc thứ 2 luôn luôn khác 0 ạ (Tương tự với các bài khác nếu được)
Em thử nha,sai thì thôi ạ.
2/ ĐK: \(-2\le x\le2\)
PT \(\Leftrightarrow\sqrt{2x+4}-\sqrt{8-4x}=\frac{6x-4}{\sqrt{x^2+4}}\)
Nhân liên hợp zô: với chú ý rằng \(\sqrt{2x+4}+\sqrt{8-4x}>0\) với mọi x thỏa mãn đk
PT \(\Leftrightarrow\frac{6x-4}{\sqrt{2x+4}+\sqrt{8-4x}}-\frac{6x-4}{\sqrt{x^2+4}}=0\)
\(\Leftrightarrow\left(6x-4\right)\left(\frac{1}{\sqrt{2x+4}+\sqrt{8-4x}}-\frac{1}{\sqrt{x^2+4}}\right)=0\)
Tới đây thì em chịu chỗ xử lí cái ngoặc to rồi..
Đúng 0
Bình luận (0)
1.\(\left(\sqrt{x+3}-\sqrt{x+1}\right)\left(x^2+\sqrt{x^2+4x+3}\right)=2x\)
ĐK \(x\ge-1\)
Nhân liên hợp ta có
\(\left(x+3-x-1\right)\left(x^2+\sqrt{x^2+4x+3}\right)=2x\left(\sqrt{x+3}+\sqrt{x+1}\right)\)
<=>\(x^2+\sqrt{\left(x+1\right)\left(x+3\right)}=x\left(\sqrt{x+3}+\sqrt{x+1}\right)\)
<=> \(\left(x^2-x\sqrt{x+3}\right)+\left(\sqrt{\left(x+1\right)\left(x+3\right)}-x\sqrt{x+1}\right)=0\)
<=> \(\left(x-\sqrt{x+3}\right)\left(x-\sqrt{x+1}\right)=0\)
<=> \(\orbr{\begin{cases}x=\sqrt{x+3}\\x=\sqrt{x+1}\end{cases}}\)
=> \(x\in\left\{\frac{1+\sqrt{13}}{2};\frac{1+\sqrt{5}}{2}\right\}\)
Vậy \(x\in\left\{\frac{1+\sqrt{13}}{2};\frac{1+\sqrt{5}}{2}\right\}\)
Đúng 0
Bình luận (0)
2. Tiếp đoạn của tth
\(\sqrt{x^2+4}=\sqrt{2x+4}+\sqrt{8-4x}\)
<=> \(x^2+4=2x+4+8-4x+2\sqrt{8\left(x+2\right)\left(x-2\right)}\)
<=> \(x^2+2x-8=4\sqrt{2\left(x+2\right)\left(2-x\right)}\)
<=>\(\left(x-2\right)\left(x+4\right)=4\sqrt{2\left(x+2\right)\left(2-x\right)}\)
<=> \(\orbr{\begin{cases}x=2\\\left(x+4\right)\sqrt{2-x}=-4\sqrt{2\left(x+2\right)}\left(2\right)\end{cases}}\)
Pt (2) vô nghiệm do \(x+4>0\)với \(x\ge-2\)
=> \(x=2\)
Vậy x=2
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
mọi người ơi, giúp em giải hpt này với ạ.
\(\left\{{}\begin{matrix}2x-y=1-2y\\3x+y=3-x\end{matrix}\right.\)
Mong mọi người giúp tôi giải hệ phương trình này:
\(\begin{cases}\sqrt{x^2+2y}+2y=\sqrt[3]{8y^3+4}+\left(x^2+2y-1\right)\sqrt{6x+4}\\\sqrt{y^2+1}+\sqrt{x-y}=2xy-x^2+\sqrt{x^2-2xy+y^2+1}+\sqrt{y}\end{cases}\)