Gọi p là chu vi của tam giác ABC ; AM , BN , CP là các trung tuyến của tam giác ABC. Chứng minh 3/4.p < AM + BN + CP < p
LP
Những câu hỏi liên quan
Cho tam giác ABC. Gọi M là trung điểm của BC. Chứng minh chu vi tam giác MNP bé hơn chu vi tam giác ABC.
Cho tam giác ABC và điểm O nằm trong tam giác. Gọi M, N, P lần lượt là trung điểm của OA, OB, OC. Biết chu vi tam giác ABC bằng 10cm. Tính chu vi tam giác MNP. Chu vi tam giác MNP: cm
Xét tam giác PAC,ta có:
{MP=MAOP=OC
=>MP = 1/2 AC
Tam giác PBC và AOB tương tự
=> Tam giác MNP đồng dạng với tam giác ABC
=> Chu vi tam giác MNP = 543/2 cm
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC và điểm O nằm trong tam giác. Gọi M, N, P lần lượt là trung điểm của OA, OB, OC. Biết chu vi tam giác ABC là 5,5m. Tính chu vi tam giác MNP.
Xét ΔOAB có
M,N lần lượt là trung điểm của OA,OB
=>MN là đường trung bình của ΔOAB
=>\(MN=\dfrac{1}{2}AB\)
Xét ΔOAC có
M,P lần lượt là trung điểm của OA,OC
=>MP là đường trung bình của ΔOAC
=>\(MP=\dfrac{1}{2}AC\)
Xét ΔOBC có
N,P lần lượt là trung điểm của OB,OC
=>NP là đường trung bình của ΔOBC
=>\(NP=\dfrac{1}{2}BC\)
Chu vi tam giác MNP là:
MN+NP+MP
\(=\dfrac{1}{2}\left(AB+CA+BC\right)\)
\(=\dfrac{1}{2}\cdot5,5=2,75\left(m\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC. gọi M, N , P lần lượt là trung điểm của ba cạnh AB, AC, BC. Gọi I là giao điểm của AP và MN
a) chứng minh IA=IP
b) chứng minh IM =IN
c) Biết chu vi của tam giác ABC là 54cm. tính chu vi tam giác MNP
Cho tam giác ABC và điểm O nằm trong tam giác. Gọi M, N, P lần lượt là trung điểm của OA, OB, OC. Biết chu vi tam giác ABC là 3m. Tính chu vi t
cho tam giác ABC. lần lượt gọi M,N,P là trung điểm của 3 cạnh AB, AC , BC. Gọi I là giao điểm của AP và MN
a) chứng minh IA=IP
b) chứng minh IM=IN
c) biết chu vi tam giác ABC là 54cm. tính chu vi tam giác MNP
a,xét tam giác ABC có MA=MB
NA=NC
Nên MN // BC Hay MI // BP; NI //PC
Xét tam giác ABP có MI // BP; NA=NB Nên MI sẽ đi qua trung điểm AP hay AI=IP(T/C đường trung bình của tam giác)
b, ta có IM là đường trung bình của tam giác ABP (theo CM trên )
\(\Rightarrow MI=\frac{1}{2}BP\)(1)
ta có IN là đường trung bình của tam giác APC (vì AN=AC; IN//PC)
\(\Rightarrow IN=\frac{1}{2}BC\) (2)
Mà BP=PC ( do p là trung điểm của BC)
từ (1);(2);(3) suy ra MI=IN
c, ta có PABC=AB+BC+AC=54 (cm) (P là chu vi bạn nhé)
ta có NP =\(\frac{1}{2}AB\)do NA=NC;PC=PB nên NP là đường trung bình của tam giác ABC
tương tự ta có \(MN=\frac{1}{2}BC\)và \(MP=\frac{1}{2}AC\)
mặt khác PMNP=MN+NP+MP=\(\frac{1}{2}BC+\frac{1}{2}AB+\frac{1}{2}AC\)=\(\frac{1}{2}\left(BC+AB+AC\right)\)=\(\frac{1}{2}.54=27\)
Vậy chu vi tam giác MNP là 27cm
Đúng 0
Bình luận (0)
Cho tam giác ABC và điểm O nằm trong tam giác đó. Gọi P, Q, R lần lượt là trung điểm của các đoạn thẳng OA, OB, OC. Tính chu vi của tam giác PQR, biết rằng tam giác ABC có chu vi p bằng 543 cm.
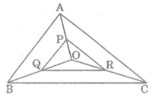
Gọi p’ là chu vi tam giác PQR.
Tacó: 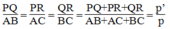
Vậy: 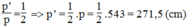
Đúng 0
Bình luận (0)
Tam giác abc, gọi m,n,p theo thứ tự là trung điểm các cạnh ab,ac,bc. tính chu vi abc biết chu vi của tam giác mnp là 15cm
mình cần gấp, cảm ơn <3
\(\dfrac{S_{MNP}}{S_{ABC}}=\dfrac{1}{2}\)
\(\Leftrightarrow S_{ABC}=2\cdot S_{MNP}=2\cdot15=30\left(cm\right)\)
Đúng 1
Bình luận (0)
cho tam giác ABC có chu vi 20cm . Gọi O là một điểm nằm trong tam giác : D ; E ; F lần lượt là trung điểm của OA ; OB ; OC . Tính chu vi tam giác DEF.
Ta có: D; E lần lượt là trung điểm của OA; OB
=> DE là đường trung bình của tam giác OAB
=> DE = 1/2 AB
Chứng minh tương tự: DF = 1/2 AC; EF = 1/2 BC
=> DE + DF + EF = 1/2 AB + 1/2 AC + 1/2 BC = 1/2 (AB + AC + BC) = 1/2 . 20 = 10 cm
Cho tam giác ABC, trực tâm H. Chu vi của tam giác ABC bằng 60cm. Gọi M,N,Q lần lượt là 3 điểm trên HA,HB,HC sao cho AN=3MH, BN=3NH, CQ=3QH. Tính chu vi của tam giác MNQ.
B
Theo bài ra, ta thấy: AM = 3 MH nên AH = 4 MH
BN = 3 NH nên BH = 4 NH
CQ = 3 QH nên CH = 4 QH
Suy ra: MH/AH = NH/BH (=1/4)
Do đó: MN song song với AB(định lí Ta-lét đảo)
MN /AB = MH/AH =1/4
Tương tự : NQ/BC = NH/BH =1/4 và MQ/AC = HQ/CH =1/4
Vì thế: MN/AB =NQ/BC = MQ/AC =1/4
Nên tam giác MNQ đồng dạng với tam giác ABC(c.c.c)
Tỉ số chu vi 2 tam giác = tỉ số 2 tam giác đồng dạng nên chu vi tam giác MNQ = 1/4 chu vi tam giác ABC
Vậy chu vi tam giác MNQ là 60:4 =15(cm)
Đúng 1
Bình luận (0)



