Tính giá trị lớn nhất của biểu thức A=x2 y với các điều kiện x,y >0 và 2x +xy =4.
BB
Những câu hỏi liên quan
20. Tìm giá trị lớn nhất của biểu thức A = x2y với các điều kiện x, y > 0 và 2x + xy = 4.
Bất đẳng thức Cauchy \(\sqrt{ab}\le\dfrac{a+b}{2}\) viết lại dưới dạng \(ab\le\left(\dfrac{a+b}{2}\right)^2\) (*) (a, b ≥ 0)
Áp dụng bất dẳng thức Cauchy dưới dạng (*) với hai số dương 2x và xy ta được :
\(2x.xy\le\left(\dfrac{2x+xy}{2}\right)^2=4\)
Dấu “ = “ xảy ra khi : 2x = xy = 4 : 2 tức là khi x = 1, y = 2=> max A = 2 <=> x = 2, y = 2.
Đúng 1
Bình luận (0)
Tìm giá trị lớn nhất của biểu thức A = x2y với các điều kiện x, y > 0 và 2x + xy = 4.
Bài 1:Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P=x^2+y^2/x^2+xy+4y^2 với x2+xy+4y^2 khác 0.Bài 2:Với x;y thỏa mãn điều kiện x^2+y^2=1.Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P=2(xy+y^2)/1+2x^2+2xy.Giúp mik nhé mai mik đi hc r
Tìm giá trị lớn nhất của biểu thức A = x2y với các điều kiện x, y > 0 và 2x + xy = 4.
Bạn nào giúp mình với nha !!!
Lớp 1 không có cánh nào phù hợp =>chịu
L
Đúng 0
Bình luận (0)
Hì hì cứ giải kiểu j cho ra là đc giúp mình vs cái lớp 1 đấy là ấn cho có thui !!!
Đúng 0
Bình luận (0)
2x+xy=4
xy=4-2x
A=x(4-2x)=4x-2x^2=2-2(x^2-2x+1)=2-2(x-1)^2
KL
Amin=2 khi x=1; y=2
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm giá trị lớn nhất của biểu thức A = x2y với các điều kiện x, y > 0 và 2x + xy = 4.
#SCREAM LAUGH !!!#
Ta có: \(2x+xy=4\)
\(\Leftrightarrow2x^2+x^2y=4x\)
\(\Leftrightarrow x^2y=4x-2x^2=-2\left(x^2-2x\right)\)
\(=-2\left(x^2-2x+1-1\right)\)
\(=-2\left[\left(x-1\right)^2-1\right]\)
\(=-2\left(x-1\right)^2+2\le2\)
Vậy \(A_{max}=2\Leftrightarrow x-1=0\Leftrightarrow x=1\)
https://olm.vn/hoi-dap/detail/71287542505.html
Áp dụng BĐT AM-GM:\(4=2x+xy\ge2\sqrt{2x^2y}\Rightarrow\sqrt{x^2y}\le\frac{4}{2\sqrt{2}}\Rightarrow x^2y\le2\)
Đẳng thức xảy ra khi \(\hept{\begin{cases}2x=xy\\2x+xy=4\end{cases}}\Leftrightarrow x=1\Rightarrow y=2\)
Vậy ...
Cho hai số thực x≠0, y≠0 thay đổi và thỏa mãn điều kiện (x+y).xyx2+y2–xy. Giá trị lớn nhất của biểu thức
M
1
x
3
+
1
y
3
là A. 18 B. 1 C. 9 D. 16
Đọc tiếp
Cho hai số thực x≠0, y≠0 thay đổi và thỏa mãn điều kiện (x+y).xy=x2+y2–xy. Giá trị lớn nhất của biểu thức M = 1 x 3 + 1 y 3 là
A. 18
B. 1
C. 9
D. 16
Đáp án D
Phương pháp giải:
Đặt ẩn phụ, đưa về hàm một biến, dựa vào giả thiết để tìm điều kiện của biến
Lời giải:
Từ giả thiết chia cả 2 vế cho x2y2 ta được : 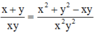
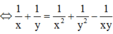
Đặt 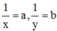 ta có
ta có ![]()
Khi đó ![]()
![]()
Ta có ![]() mà
mà 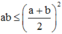
nên ![]()
![]()
![]()
Dấu đẳng thức xảy ra khi 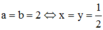 . Vậy Mmax = 16
. Vậy Mmax = 16
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất của A = x2y với các điều kiện x, y > 0 và 2x + xy = 4
Áp dụng bđt \(\left(a+b\right)^2\ge4ab\) , ta có :
\(16=\left(2x+xy\right)^2\ge4.2x.xy\Leftrightarrow8x^2y\le16\Leftrightarrow x^2y\le2\)
A đạt giá trị lớn nhất bằng 2 khi x = 1, y = 2
Đúng 0
Bình luận (0)
1) Giải pt: ![]() .
.
2) Tìm giá trị lớn nhất của biểu thức A = x2y với các điều kiện x, y > 0 và 2x + xy = 4.
Giúp e vs plzz sắp thi vào 10 chuyên rồi
Cho x,y là các số thực thay đổi thỏa mãn điều kiện x2 +y2+xy=3.Tìm giá trị lớn nhất và nhỏ nhất của biểu thức x2+y2-xy
\(x^2+y^2+xy=3\)
Có \(x^2+y^2\ge2xy\) \(\Rightarrow3=x^2+y^2+xy\ge2xy+xy\) \(\Leftrightarrow xy\le1\)
\(x^2+y^2\ge-2xy\) \(\Rightarrow3=x^2+y^2+xy\ge-2xy+xy\) \(\Leftrightarrow-3\le xy\)
Đặt A= \(x^2+y^2-xy=\left(3-xy\right)-xy=3-2xy\)
mà \(-3\le xy\le1\) \(\Rightarrow9\ge3-2xy\ge1\)
=> minA=1 <=> \(\left\{{}\begin{matrix}xy=1\\x=y\end{matrix}\right.\) <=>x=y=1
maxA=9 <=>\(\left\{{}\begin{matrix}xy=-3\\x=-y\end{matrix}\right.\) <=>\(\left(x;y\right)=\left(\sqrt{3};-\sqrt{3}\right);\left(-\sqrt{3};\sqrt{3}\right)\)
Đúng 2
Bình luận (0)
Đặt \(P=x^2+y^2-xy\)
\(\Rightarrow\dfrac{P}{3}=\dfrac{x^2+y^2-xy}{3}=\dfrac{x^2+y^2-xy}{x^2+y^2+xy}\)
\(\dfrac{P}{3}=\dfrac{3x^2+3y^2-3xy}{3\left(x^2+y^2+xy\right)}=\dfrac{x^2+y^2+xy+2\left(x^2+y^2-2xy\right)}{3\left(x^2+y^2+xy\right)}\)
\(\dfrac{P}{3}=\dfrac{1}{3}+\dfrac{2\left(x-y\right)^2}{3\left(x^2+y^2+xy\right)}\ge\dfrac{1}{3}\Rightarrow P\ge1\)
\(P_{min}=1\) khi \(x=y=1\)
\(\dfrac{P}{3}=\dfrac{x^2+y^2-xy}{x^2+y^2+xy}=\dfrac{3\left(x^2+y^2+xy\right)-2\left(x^2+y^2+2xy\right)}{x^2+y^2+xy}=3-\dfrac{2\left(x+y\right)^2}{x^2+y^2+xy}\le3\)
\(\Rightarrow P\le9\)
\(P_{max}=9\) khi \(\left(x;y\right)=\left(\sqrt{3};-\sqrt{3}\right);\left(-\sqrt{3};\sqrt{3}\right)\)
Đúng 3
Bình luận (0)


