Giải bất phương trình sau và biểu diễn nghiệm trên trục số
4x-1>3x+5
NN
Những câu hỏi liên quan
Giải bất phương trình và biểu diễn tập nghiệm trên trục số
4x + 5 ≥ 12x - 11
4x + 5 ≥ 12x - 11
\(\Leftrightarrow4x+5-12x+11\ge0\)
\(\Leftrightarrow16-8x\ge0\)
\(\Leftrightarrow8x\ge16\)
\(x\ge2\)
Đúng 2
Bình luận (0)
`4x + 5 >= 12x - 11`
`16 >= 8x`
`=> x >= 2`.
Đúng 2
Bình luận (0)
Bài 2: ( 1 điểm) Giải bất phương trình sau và biểu diễn tập nghiệm trên trục số. 3x + 5 - 1
Bài 3 :Cho bất phương trình : 3x(2x + 5) x(6x -1) + 4a) Giải bất phương trình và biểu diễn tập nghiệm trên trục số.b) Tìm nghiệm nguyên nhỏnhất của bất phương trình trên.
Đọc tiếp
Bài 3 :Cho bất phương trình : 3x(2x + 5) x(6x -1) + 4
a) Giải bất phương trình và biểu diễn tập nghiệm trên trục số.
b) Tìm nghiệm nguyên nhỏnhất của bất phương trình trên.
Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số: a, 3x -11 >5 -x
\(a,3x-11>5-x\\ \Leftrightarrow3x+x>5+11\\ \Leftrightarrow4x< 16\\ \Leftrightarrow x>4\)
Vậy bất phương trình có nghiệm là: \(S=\left\{x|x>4\right\}\)
biểu diễn
Đúng 1
Bình luận (0)
giải bất phương trình sau đây và biểu diễn tập nghiệm trên trục số
\(\dfrac{x-1}{3}\)-\(\dfrac{3x+5}{2}\)≥1-\(\dfrac{4x+5}{6}\)
Ta có: \(\dfrac{x-1}{3}-\dfrac{3x+5}{2}\ge1-\dfrac{4x+5}{6}\)
\(\Leftrightarrow2\left(x-1\right)-3\left(3x+5\right)\ge6-4x-5\)
\(\Leftrightarrow2x-2-9x-15-6+4x+5\ge0\)
\(\Leftrightarrow-3x\ge18\)
hay \(x\le-6\)
Đúng 0
Bình luận (0)
Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số:
a) 3 x + 7 > x + 5 b) x−4≤−3x+6.
Giải bất phương trình sau và biểu diễn nghiệm trên trục số 3 x - 1 4 ≥ 2
Ta có: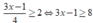
⇔ 3x - 1 > 8
⇔ 3x ≥ 9 ⇔ x ≥ 3
Vậy x ≥ 3 là nghiệm của bất phương trình.
Ta biểu diễn tập nghiệm trên trục số như sau:
Đúng 0
Bình luận (0)
Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số:a)
3
x
−
3
x
+
9
;
b)
x
−
4
x
−
1
≥
5
−
x
1
−
x
Đọc tiếp
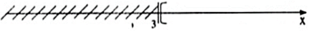
Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số:
a) 3 x − 3 > x + 9 ; b) x − 4 x − 1 ≥ 5 − x 1 − x
Giải bất phương trình sau đây và biểu diễn tập nghiệm trên trục số : x - 1 3 - 3 x + 5 2 ≥ 1 - 4 x + 5 6
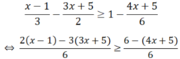
⇔ 2x - 2 - 9x - 15 ≥ 6 - 4x - 5
⇔ 2x - 9x + 4x ≥ 6 - 5 + 2 + 15
⇔ -3x ≥ 18
⇔ x ≤ -6
Vậy tập nghiệm của phương trình là S= {x|x ≤ -6}
Biểu diễn nghiệm trên trục số:
Đúng 0
Bình luận (0)