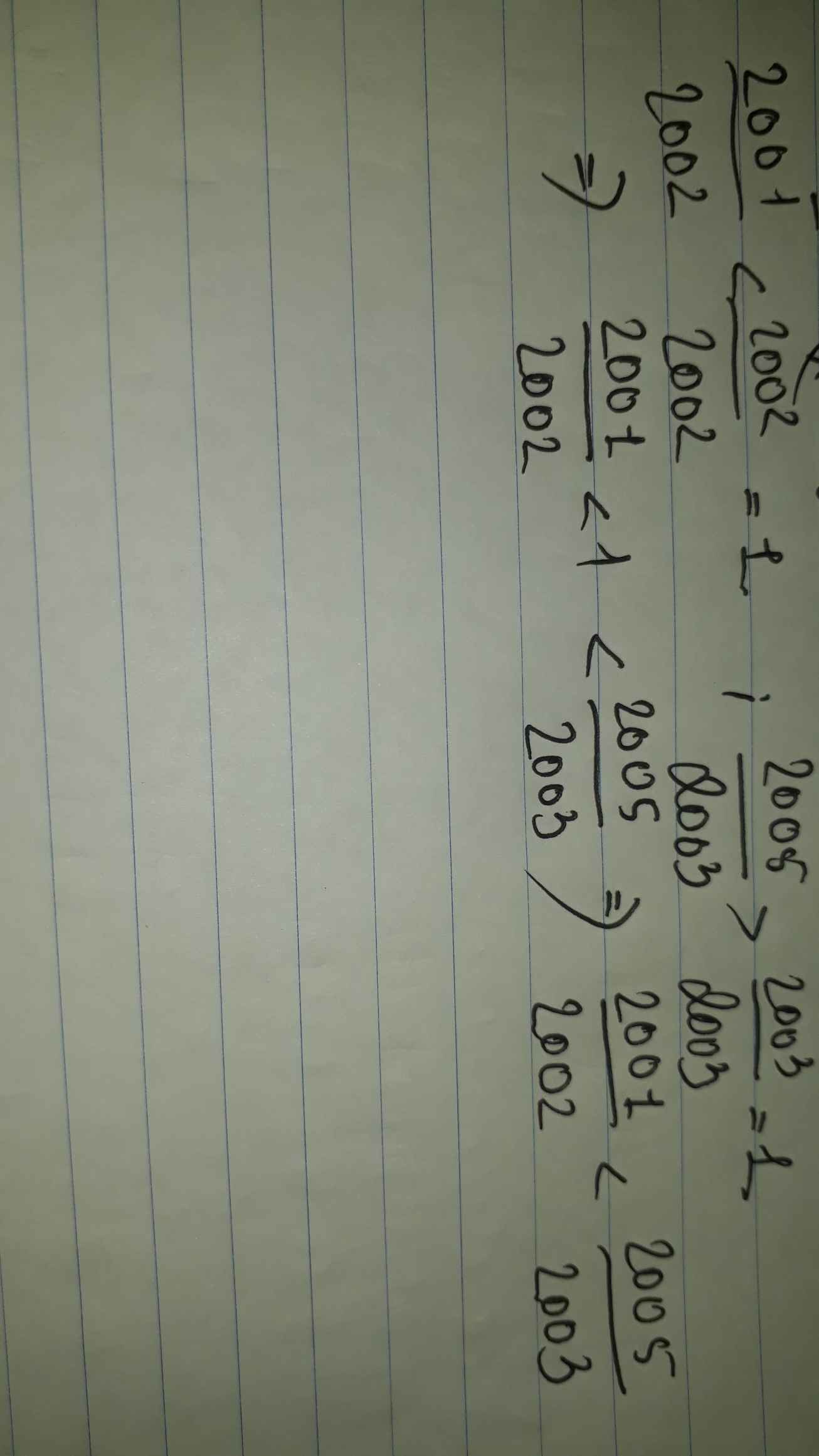So sánh phân số \(\dfrac{2001}{2002}\)và\(\dfrac{2021}{2003}\)
HV
Những câu hỏi liên quan
ko quy đồg so sánh (2001+2002)/(2002+2003) và 2001/2002 + 2002/2003
Tham khảo :
Sứa , san hô , hải quỳ , thủy tức , sứa tu dài ,...
Đúng 0
Bình luận (0)
\(\dfrac{2001+2002}{2002+2003}< \dfrac{2001}{2002}+\dfrac{2002}{2003}\)
Đúng 0
Bình luận (0)
So Sánh :A=2001/2003 và B=2001+2002/2002+2003
\(\dfrac{2002}{2003}\) và \(\dfrac{14}{13}\)
So sánh
Ta có: \(\dfrac{2002}{2003}< \dfrac{14}{13}\) vì \(\dfrac{2002}{2003}< 1\), \(\dfrac{14}{13}>1\)
Đúng 0
Bình luận (0)
\(\frac{2001}{2002}và\frac{2002}{2003}\)
so sánh 2 phân số trên
2001/2002=1-1/2002
2002/2003=1-1/2003
vi 1/2003<1/2002 nen 2001/2002<2002/2003
Đúng 0
Bình luận (0)
Ta có: 2003 x 2001 < 2002 x 2002
=> \(\frac{2001}{2002}\)<\(\frac{2002}{2003}\)
Đúng 0
Bình luận (0)
2 phân số trên: 2001/2002 = 2002/2003
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giải phương trình sau :
\(\dfrac{x-4}{2001}+\dfrac{x-3}{2002}+\dfrac{x-2}{2003}=\dfrac{x-2003}{2}+\dfrac{x-2002}{3}+\dfrac{x-2001}{4}\)
\(\dfrac{x-4}{2001}\)- 1 +\(\dfrac{x-3}{2002}\)-1 + \(\dfrac{x-2}{2003}\)-1 =\(\dfrac{x-2003}{2}\)-1 + \(\dfrac{x-2002}{3}\)-1 +\(\dfrac{x-2001}{4}\)-1 <=> \(\dfrac{x-2005}{2001}\)+\(\dfrac{x-2005}{2002}\)+\(\dfrac{x-2005}{2003}\)-\(\dfrac{x-2005}{2}\)-\(\dfrac{x-2005}{3}\)-\(\dfrac{x-2005}{4}\)= 0 <=> (x-2005). (\(\dfrac{1}{2001}\)+\(\dfrac{1}{2002}\)+\(\dfrac{1}{2003}\)-\(\dfrac{1}{2}\)-\(\dfrac{1}{3}\)-\(\dfrac{1}{4}\)) =0 <=> x-2005=0 ( vì \(\dfrac{1}{2001}\) +\(\dfrac{1}{2002}\) +\(\dfrac{1}{2003}\)- \(\dfrac{1}{2}\) -\(\dfrac{1}{3}\)- \(\dfrac{1}{4}\) khác 0) =>x = 2005
Đúng 0
Bình luận (0)
x-4/2001+ x-3/2002 + x-2/2003= x-2003/2 + x-2002/3 + x-2001/4
<=>(x-4/2001 -1)+(x-3/2002 -1)+(x-2/2003 -1)-(x-2003/2 -1)+
(x-2002/3 -1)+(x-2001/4 -1) =0
<=>x-2005/2001+ x-2005/2002+ x-2005/2003- x-2005/2-
x-2005/3- x-2005/4 =0
<=>(x-2005).(1/2001+1/2002+1/2003- 1/2- 1/3- 1/4)=0
<=>x-2005=0 (vì 1/2001+1/2002+1/2003-1/2-1/3-1/4)
<=>x=2005
Vậy pt có nghiệm là x=2005
Đúng 0
Bình luận (0)
\(\dfrac{x-4}{2001}+\dfrac{x-3}{2002}+\dfrac{x-2}{2003}=\dfrac{x-2003}{2}+\dfrac{x-2002}{3}+\dfrac{x-2001}{4}\)
\(\Leftrightarrow\dfrac{x-4}{2001}-1+\dfrac{x-3}{2002}-1+\dfrac{x-2}{2003}-1=\dfrac{x-2003}{2}-1+\dfrac{x-2002}{3}-1+\dfrac{x-2001}{4}-1\)
\(\Leftrightarrow\dfrac{x-2005}{2001}+\dfrac{x-2005}{2002}+\dfrac{x-2005}{2003}-\dfrac{x-2005}{2}-\dfrac{x-2005}{3}-\dfrac{x-2005}{4}=0\)
\(\Leftrightarrow\left(x-2005\right)\left(\dfrac{1}{2001}+\dfrac{1}{2002}+\dfrac{1}{2003}-\dfrac{1}{2}-\dfrac{1}{3}-\dfrac{1}{4}\ne0\right)=0\)
\(\Leftrightarrow x-2005=0\)
\(\Leftrightarrow x=2005\)
Vậy nghiệm của PT là \(x=2005\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
so sánh A= \(\dfrac{2003^{2003}+1}{2003^{2004}+1}\)
B=
\(\dfrac{2003^{2002}+1}{2003^{2003}+1}\)
Ta có: \(2003^{2003}+1=2003^{2002+1}+1và2003^{2004}+1=2003^{2003+1}+1\)
\(\Rightarrow A>B\)
Đúng 1
Bình luận (0)
Không quy đồng mẫu số so sánh các phân số sau:
a,199/200 và 200/201 B, 2001/2002 và 2002/203 c,2021/2020 và 2020/2019 d,199/198 và 200/199
\(a,\dfrac{199}{200}=1-\dfrac{1}{200};\dfrac{200}{201}=1-\dfrac{1}{201}\\ Vì:\dfrac{1}{200}>\dfrac{1}{201}\\ \Rightarrow1-\dfrac{1}{200}< 1-\dfrac{1}{201}\\ Vậy:\dfrac{199}{200}< \dfrac{200}{201}\\ b,\dfrac{2001}{2002}=1-\dfrac{1}{2002};\dfrac{2002}{2003}=1-\dfrac{1}{2003}\\ Vì:\dfrac{1}{2002}>\dfrac{1}{2003}\Rightarrow1-\dfrac{1}{2002}< 1-\dfrac{1}{2003}\\ Vậy:\dfrac{2001}{2002}< \dfrac{2002}{2003}\)
Đúng 2
Bình luận (0)
\(c,\dfrac{2021}{2020}=1+\dfrac{1}{2020};\dfrac{2020}{2019}=1+\dfrac{1}{2019}\\ Vì:\dfrac{1}{2020}< \dfrac{1}{2019}\\ Nên:1+\dfrac{1}{2020}< 1+\dfrac{1}{2019}\\ Vậy:\dfrac{2021}{2020}< \dfrac{2020}{2019}\\ d,\dfrac{199}{198}=1+\dfrac{1}{198};\dfrac{200}{199}=1+\dfrac{1}{199}\\ Vì:\dfrac{1}{198}>\dfrac{1}{199}\\ Nên:1+\dfrac{1}{198}>1+\dfrac{1}{199}\\ Vậy:\dfrac{199}{198}>\dfrac{200}{199}\)
Đúng 1
Bình luận (0)
So sánh 2 phân số; -2001/2002 và -2002/2003
- Giúp mình vs ạ?
Bài làm:
Ta có: \(\frac{2001}{2002}< \frac{2002}{2003}\)
\(\Leftrightarrow-\frac{2001}{2002}>-\frac{2002}{2003}\)
so sánh các số hữu tỉ 2001/2002 và 2005/2003
ta có\(\dfrac{2001}{2002}< 1\)và\(\dfrac{2005}{2003}>1\)
\(\Rightarrow\dfrac{2001}{2002}< \dfrac{2005}{2003}\)
Đúng 1
Bình luận (0)
Ta có: \(\dfrac{2001}{2002}< 1\)
mà \(1< \dfrac{2005}{2003}\)
nên \(\dfrac{2001}{2002}< \dfrac{2005}{2003}\)
Đúng 0
Bình luận (0)