MV
Những câu hỏi liên quan
Cho tam giác ABC nhọn có ABAC, tia phân giác góc BAC cắt BC tại D. Trên AC lấy E sao cho AEAB. Tia ED cắt AB tại M. Chứng minh: a)Tam giác ABDtam giác AED. b)AMAC và AD là đường trung trực của MC. c)BDDC.
Đọc tiếp
Cho tam giác ABC nhọn có AB<AC, tia phân giác góc BAC cắt BC tại D. Trên AC lấy E sao cho AE=AB. Tia ED cắt AB tại M. Chứng minh: a)Tam giác ABD=tam giác AED. b)AM=AC và AD là đường trung trực của MC. c)BD<DC.
Cho tam giác nhọn ABC có AB=AC. Vẽ tiaphaan giác AD của góc BẠC (Dthuoocj cạnh BC)
chứng minh tâm giác abd= tam giác acd và AD vuông góc với BC
Xem chi tiết
cho tam giác ABC nhọn ( AB < AC ) . Vẽ ra phía ngoài 2 tam giác ABD và tam giác ACE.
a) tam giác DAC = tam giác BAE
b)DC vuông góc với BE
Cho tam giác nhọn ABC, AB<AC, đường cao AH. a) c/m góc BAH < góc HAC. b) Trên đoạn HC sao cho HD=HB. C/m ABD là tam giác cân
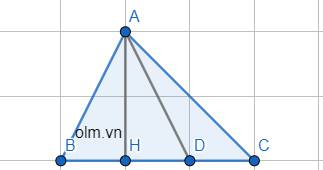
Vì AH \(\perp\) BC \(\equiv\) H nên:
BH là hình chiếu của AB trên BC
HC là hình chiếu của AC trên BC
AB < AC => BH < HC ( Mối quan hệ đường xiên và hình chiếu )
\(\widehat{BAH}\) Đối diện cạnh BH
\(\widehat{HAC}\) Đối diện cạnh HC
mà BH < HC ( chứng minh trên)
=> \(\widehat{BAH}\) < \(\widehat{HAC}\) ( mối quan hệ giữa cạnh và góc trong tam giác)
Ta có : HD = HB (gt) (1)
AH \(\perp\) BD \(\equiv\) H (2)
Từ (1) và (2) ta có : \(\Delta\) ABD cân tại A vì AH vừa là đường cao vừa là đường trung tuyến của \(\Delta\) ABD
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn, hai đường cao BD và CE (D=AC, E=AB). a) Chứng minh: tam giác ABD đồng dạng với tam giác ACE. b) Chứng minh: góc EDB bằng góc ECB
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc DAB chung
=>ΔADB đồng dạng với ΔAEC
b: góc BEC=góc BDC=90 độ
=>BEDC nội tiếp
=>góc EDB=góc ECB
Đúng 0
Bình luận (0)
Bài 4: Cho tam giác nhọn ABC, kẻ BM vuông góc AC, CN vuông góc AB. Trên tia đối của tia BM lấy điểm D sao cho BD=AC, trên tia đối của tia CN lấy điểm E sao cho CE=AB. Chứng minh:
a) Góc ACE= góc ABD
b) Tam giác ABD = tam giác ECA
c) Tam giác AED là tam giác vuông cân
Cho tam giác abc nhọn (AB<AC). Kẻ các đường cao BD, CF cắt nhau tại H. CM: a) Tam giác ABD đồng dạng tam giác ACE
b) tam giác AEH đồng dạng tam giác CEB
sửa lại đề :
Cho tam giác abc nhọn (AB<AC). Kẻ các đường cao BD, CE cắt nhau tại H.
CM: a) Tam giác ABD đồng dạng tam giác ACE
b) tam giác AEH đồng dạng tam giác CEB
a,Xét \(\Delta ABD\)và \(\Delta ACE\)có :
\(\widehat{ADB}=\widehat{AEC}=90^0\)
\(\widehat{BAC}\)chung
\(\Rightarrow\Delta ABD~\Delta ACE\left(g.g\right)\)
Cho tam giác ABC nhọn (AB<AC). Vẽ về phía ngoài tam giác ABC các tam giác vuông cân tại A là ABD, ACE và hình bình hành ADKE. Chứng minh:
a. KA=BC
b. KA vuông góc BC
Cho tam giác ABC nhọn ( AB< AC) , AD là phân giác của BAC . Trên cạnh AC lấy
điểm E sao cho: AE=AB.
a) Chứng minh: tam giác ABD= tam giác AED
b) Chứng minh: AD vuông góc với BE
c) Gọi N là giao điểm của DE với AB. Chứng minh: NB= EC
a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn có ba đường cao AD, BE, CF với D thuộc BC, E thuộc AC, F thuộc AB, Gọi H là trực tâm của tam giác ABC. Chững minh rằng tam giác ABD đồng dạng với tam giác CHD
Xét ΔABD vuông tại D và ΔCHD vuông tại D có
góc BAD=góc HCD
=>ΔABD đồng dạng vớiΔCHD
Đúng 0
Bình luận (0)

