Giải giúp mk câu 6e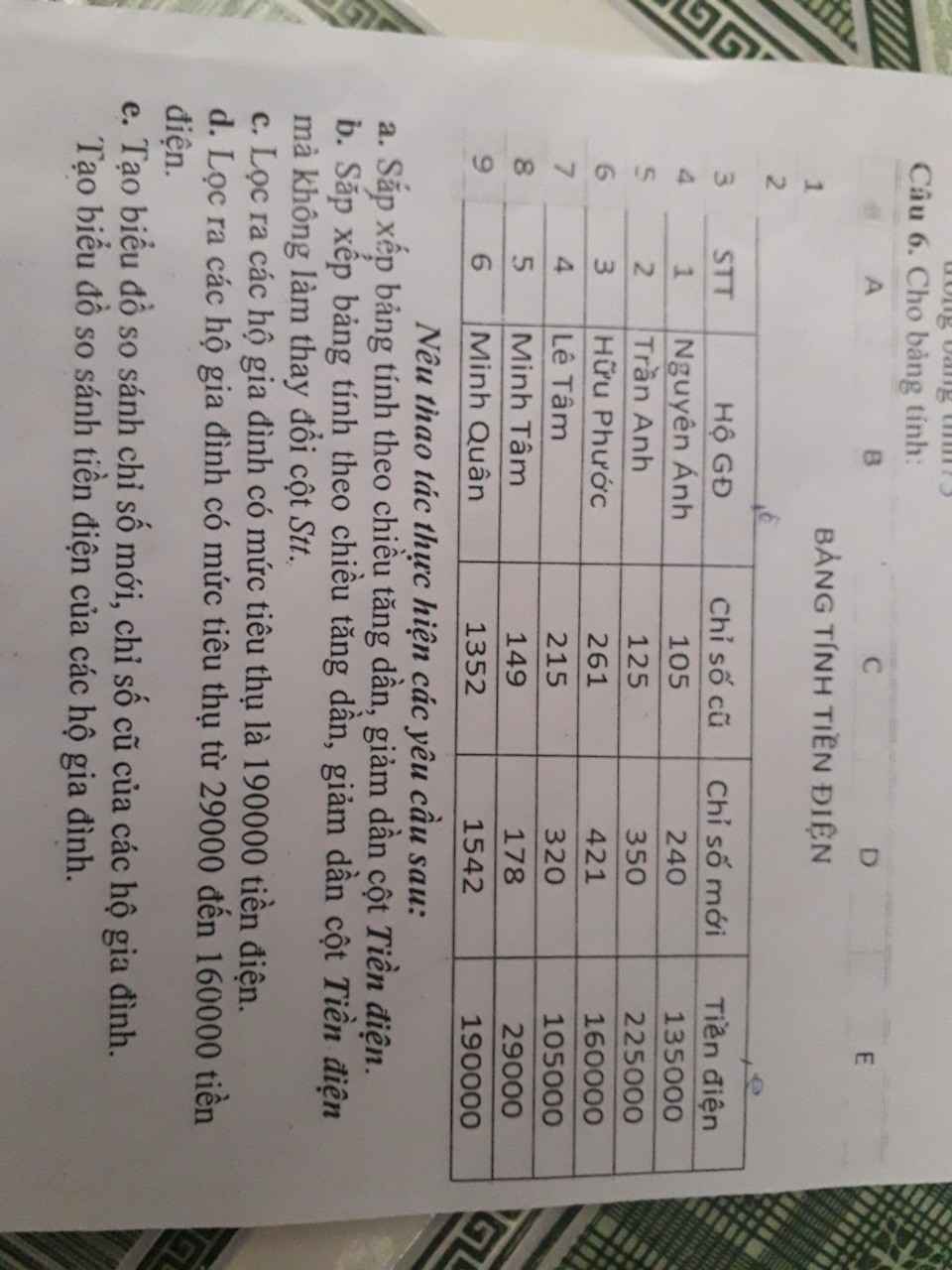
LB
Những câu hỏi liên quan
Hello ! Mọi người giải giúp mk câu này nhé !
abc x aa x bc = abcabc
GIẢI NHANH GIÚP MK NHÉ , MK TYM CHO
Giải giúp mk 2 bài này với ạ mk đag cần gấp . dịch giúp mk 4 câu của part 7
P6:
1. big
2. been
3. bought
4. people
P7:
1. T
2. F
3. F
4. F
Đúng 1
Bình luận (1)
Giúp mk câu II nha giải thích hội mk luôn ạ
II)
1 . B (đọc là /ð/ )
2 . D ( đọc là/t/ )
3 . C ( đọc là /i/ )
4 . B ( đọc là /SH/ )
Đúng 1
Bình luận (0)
Giải nhanh giúp mk nha. Ko cần giải câu 193

Giải giúp mk câu 62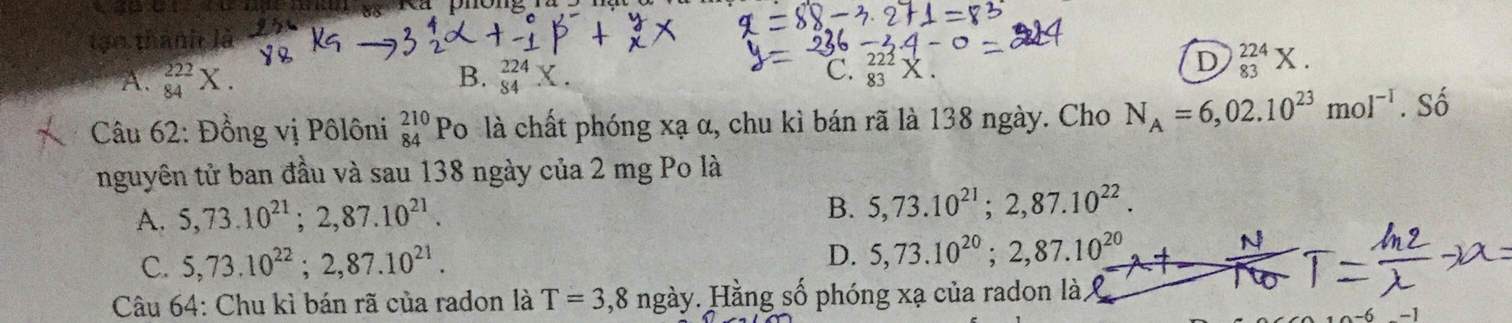
Giải giúp mk câu này!
\(=120:\left\{54-\left[25-9+8\right]\right\}\)
=120:(54-25+9-8)
=120:30
=4
Đúng 0
Bình luận (0)
Giải giúp mk câu 5 vs ạ. Mk đang cần gấp. Thanks!
Đoạn AB: nước nóng lên.
Đoạn BC: nước sôi.
Đoạn CD: nước nguội đi.
Đúng 1
Bình luận (1)

giúp mk giải chi tiết 4 câu trên ạ
mk cảm ơn
\(5;;\sqrt{\left(x+5\right)\left(3x+4\right)}>4\left(x-1\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}4\left(x-1\right)\le0\\\left(x+5\right)\left(3x+4\right)\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}4\left(x-1\right)\ge0\\\left(x+5\right)\left(3x+4\right)\ge0\\\left(x+5\right)\left(3x+4\right)>16\left(x-1\right)^2\end{matrix}\right.\end{matrix}\right.\)
\(TH:\left\{{}\begin{matrix}4\left(x-1\right)\le0\\\left(x+5\right)\left(3x+4\right)\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\le1\\\left[{}\begin{matrix}x\le-5\\x\ge-\dfrac{4}{3}\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow x\in(-\infty;-5]\cup\left[-\dfrac{4}{3};1\right]\left(1\right)\)
\(TH:\left\{{}\begin{matrix}4\left(x-1\right)\ge0\\\left(x+5\right)\left(3x+4\right)\ge0\\\left(x+5\right)\left(3x+4\right)>16\left(x-1\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge1\\\left[{}\begin{matrix}x\le-5\\x\ge-\dfrac{4}{3}\end{matrix}\right.\\-\dfrac{1}{13}< x< 4\\\end{matrix}\right.\)\(\Rightarrow x\in[1;4)\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow x\in(-\infty;5]\cup[\dfrac{-4}{3};4)\)
Đúng 0
Bình luận (0)
\(6;;;;\sqrt{7x+7}+\sqrt{7x-6}+2\sqrt{49x^2+7x-42}< 181-14x\)
(đoạn 49x^2+7x+42 chắc bạn viết sai đề dấu"-" thành "+")
\(đk:\left\{{}\begin{matrix}7x+7\ge0\\7x-6\ge0\end{matrix}\right.\) \(\Leftrightarrow x\ge\dfrac{6}{7}\)
\(bpt\Leftrightarrow\sqrt{7x+7}+\sqrt{7x-6}+2\sqrt{\left(7x+7\right)\left(7x-6\right)}+14x+1< 182\left(1\right)\)
\(đặt:\sqrt{7x+7}+\sqrt{7x-6}=t>0\)
\(\Rightarrow t^2=14x+1+2\sqrt{\left(7x+7\right)\left(7x-6\right)}\)
\(\Rightarrow\left(1\right)\Leftrightarrow t^2+t< 182\Leftrightarrow-14< t< 13\)
\(\Rightarrow\sqrt{7x+7}+\sqrt{7x-6}< 13\Leftrightarrow14x+1+2\sqrt{\left(7x+7\right)\left(7x-6\right)}< 169\)
\(\Leftrightarrow2\sqrt{\left(7x+7\right)\left(7x-6\right)}< 168-14x\)
\(\Leftrightarrow\left\{{}\begin{matrix}168-14x\ge0\\\left(7x+7\right)\left(7x-6\right)\ge0\\4\left(7x+7\right)\left(7x-6\right)< \left(168-14x\right)^2\\\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le12\\\left[{}\begin{matrix}x\le-1\\x\ge\dfrac{6}{7}\end{matrix}\right.\\x< 6\\\end{matrix}\right.\)\(\Rightarrow\dfrac{6}{7}\le x< 6\)
Đúng 0
Bình luận (0)
\(7;\) \(3\sqrt{x}+\dfrac{3}{2\sqrt{x}}< 2x+\dfrac{1}{2x}-1\left(đk:x>0\right)\)
\(\Leftrightarrow3\left(\sqrt{x}+\dfrac{1}{2\sqrt{x}}\right)< 2\left(x+\dfrac{1}{4x}\right)-1\left(1\right)\)
\(đặt:\sqrt{x}+\dfrac{1}{2\sqrt{x}}=t>0\)
\(\Leftrightarrow t^2=\sqrt{x}^2+2.\sqrt{x}.\dfrac{1}{2\sqrt{x}}+\left(\dfrac{1}{2\sqrt{x}}\right)^2=x+\dfrac{1}{4x}+1\)
\(\Rightarrow x+\dfrac{1}{4x}=t^2-1\)
\(\left(1\right)\Leftrightarrow3t< 2\left(t^2-1\right)-1\)
\(\Leftrightarrow2t^2-3t-3>0\Leftrightarrow\left[{}\begin{matrix}t< \dfrac{3-\sqrt{33}}{4}\\t>\dfrac{3+\sqrt{33}}{4}\end{matrix}\right.\)
\(\Rightarrow\sqrt{x}+\dfrac{1}{2\sqrt{x}}>\dfrac{3+\sqrt{33}}{4}\)
\(\Leftrightarrow\dfrac{2x+1}{2\sqrt{x}}>\dfrac{3+\sqrt{33}}{4}\)
\(\Leftrightarrow\sqrt{x}< \dfrac{2\left(2x+1\right)}{3+\sqrt{33}}\Leftrightarrow\left\{{}\begin{matrix}x>0\\2\left(2x+1\right)\ge0\\x< \left[\dfrac{2\left(2x+1\right)}{3+\sqrt{33}}\right]^2\\\end{matrix}\right.\)
đến đây dễ dàng rồi như mấy ý trên bạn tự giải quyết để tìm ra x
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giúp mk giải bài 2 câu 1 với mk đang cần gấp 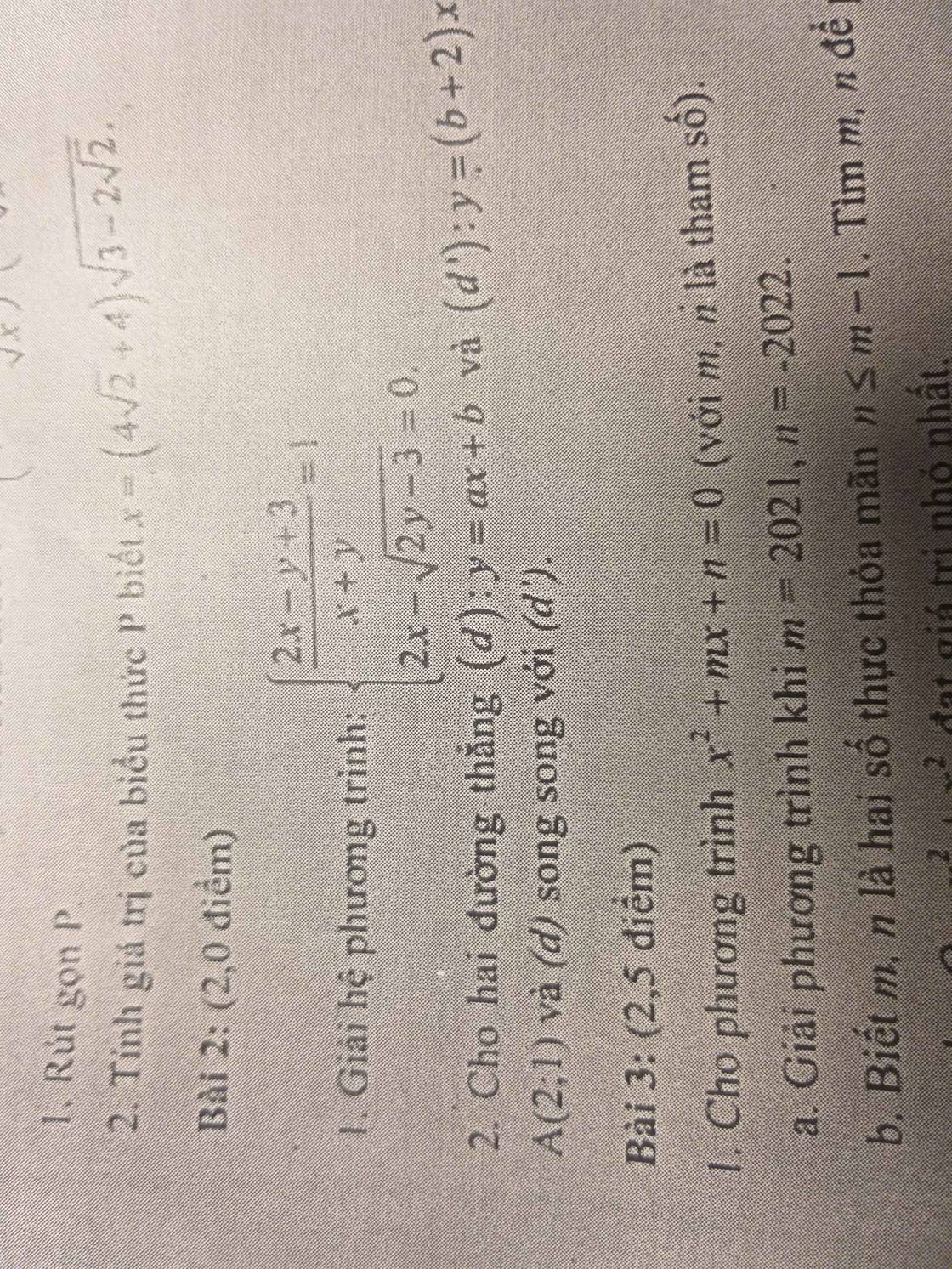
ĐK: \(\left\{{}\begin{matrix}x\ne-y\\y\ge\dfrac{3}{2}\end{matrix}\right.\).
\(\left\{{}\begin{matrix}\dfrac{2x-y+3}{x+y}=1\\2x-\sqrt{2y-3}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2x-y+3}{x+y}-1=0\\2x-\sqrt{2y-3}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2x-y+3}{x+y}-\dfrac{x+y}{x+y}=0\\2x-\sqrt{2y-3}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x-y+3-x-y=0\\2x-\sqrt{2y-3}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-2y+3=0\\2x-\sqrt{2y-3}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-\left(2y-3\right)=0\\2x-\sqrt{2y-3}=0\end{matrix}\right..\)
Đặt a = x, b = \(\sqrt{2y-3}\).
Hệ phương trình trở thành: \(\left\{{}\begin{matrix}a-b^2=0\\2a-b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=b^2\\2b^2-b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=b^2\\b\left(2b-1\right)=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=b^2\\\left[{}\begin{matrix}b=0\\b=\dfrac{1}{2}\end{matrix}\right.\end{matrix}\right.\left\{{}\begin{matrix}\left[{}\begin{matrix}a=0\\a=\dfrac{1}{4}\end{matrix}\right.\\\left[{}\begin{matrix}b=0\\b=\dfrac{1}{2}\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x=0\\x=\dfrac{1}{4}\end{matrix}\right.\\\left[{}\begin{matrix}y=\dfrac{3}{2}\\2y-3=\dfrac{1}{4}\end{matrix}\right.\end{matrix}\right.\left\{{}\begin{matrix}\left[{}\begin{matrix}x=0\\x=\dfrac{1}{4}\end{matrix}\right.\\\left[{}\begin{matrix}y=\dfrac{3}{2}\\2y=\dfrac{13}{4}\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x=0\\x=\dfrac{1}{4}\end{matrix}\right.\\\left[{}\begin{matrix}y=\dfrac{3}{2}\\y=\dfrac{13}{8}\end{matrix}\right.\end{matrix}\right..\)
Vậy hệ phương trình có nghiệm (x;y) \(\in\) \(\left\{\left(0;\dfrac{3}{2}\right),\left(\dfrac{1}{4};\dfrac{13}{8}\right)\right\}\).
Đúng 0
Bình luận (0)





