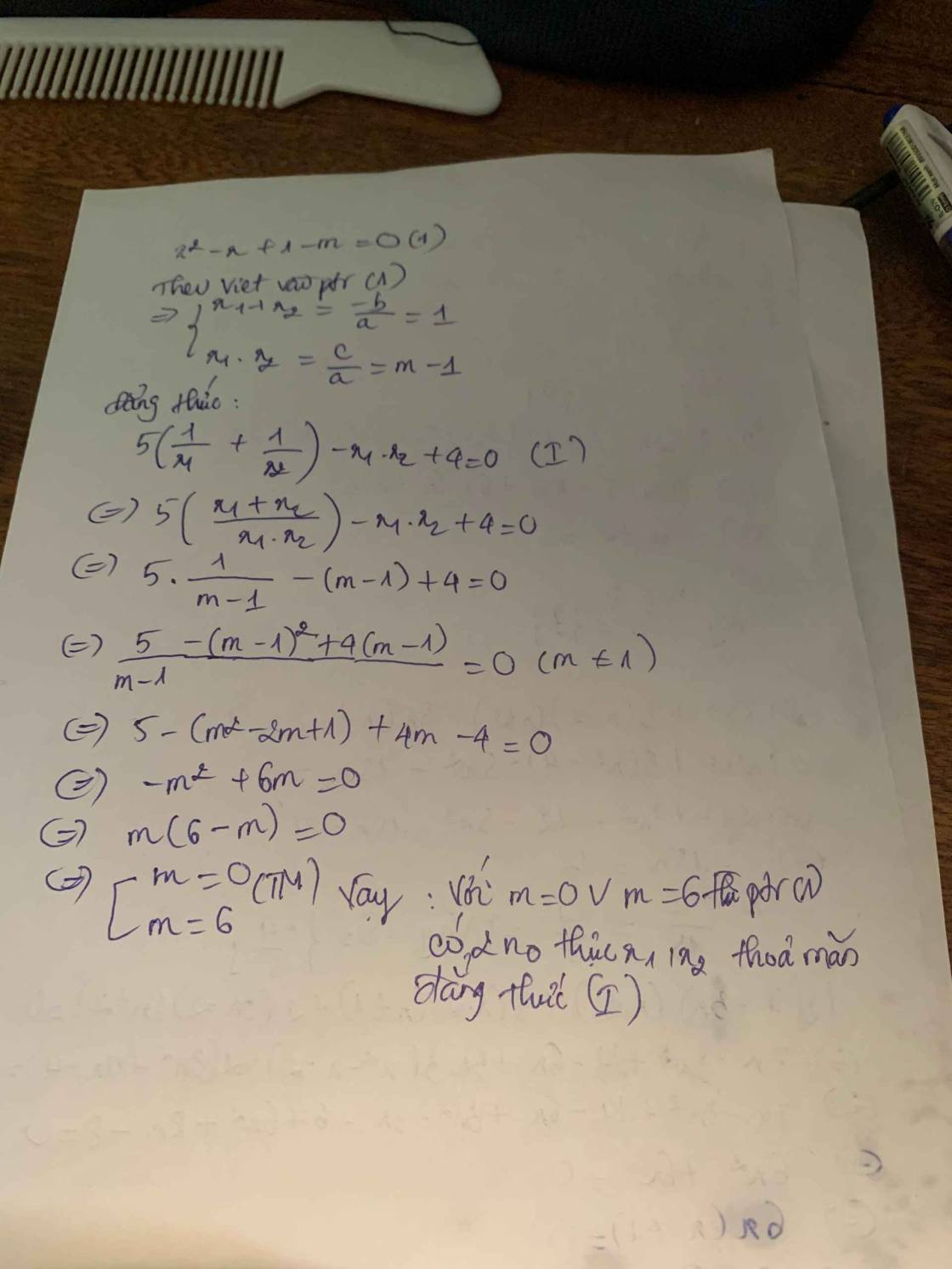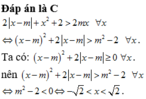Xác định giá trị của m để bất đẳng thức 3mx>x+2 thỏa mãn với mọi giá trị của x>1
NM
Những câu hỏi liên quan
Xác định các giá trị của m để ptr \(x^2-x+1-m=0\) có 2 nghiệp thực x1,x2 thỏa mãn đẳng thức \(5\left(\dfrac{1}{x_1}+\dfrac{1}{x_2}\right)-x_1x_2+4=0\)
help me: tìm n biết 2^n + 3^n = 5^n với n E N
Đúng 0
Bình luận (0)
cho G = x-2/x+1
Tìm x để đẳng thức G.(x+1)=m.(x2-1)-3 thỏa mãn với mọi giá trị của m
Xác định các giá trị của m để phương trình \(x^2-x+1-m=0\) có 2 nghiệm thực \(x_1,x_2\) thỏa mãn đẳng thức \(5\left(\dfrac{1}{x_1}+\dfrac{1}{x_2}\right)-x_1x_2+4=0\)
\(x^2-x+1-m=0\)
Theo Vi - ét, ta có :
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=1\\x_1x_2=\dfrac{c}{a}=1-m\end{matrix}\right.\)
Ta có :
\(5\left(\dfrac{1}{x_1}+\dfrac{1}{x_2}\right)-x_1x_2+4=0\)
\(\Leftrightarrow5\left(\dfrac{x_2+x_1}{x_1x_2}\right)-x_1x_2+4=0\)
\(\Leftrightarrow5\left(\dfrac{1}{1-m}\right)-\left(1-m\right)+4=0\)
\(\Leftrightarrow\dfrac{5}{1-m}-1+m+4=0\)
\(\Leftrightarrow\dfrac{5}{1-m}+m+3=0\)
\(\Leftrightarrow\dfrac{5+m\left(1-m\right)+3\left(1-m\right)}{1-m}=0\)
\(\Leftrightarrow5+m-m^2+3-3m=0\)
\(\Leftrightarrow-m^2-2m+8=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=2\\m=-4\end{matrix}\right.\)
Đúng 2
Bình luận (1)
Câu 1 a.tìm tất cả các giá trị của tham số m để bất phương trình mx²+3mx+(m+1)>0 nghiệm đúng với mọi số thực x? b.tìm các giá trị của m để biểu thức sau luôn âm:g(x)=(m-4)x²+(2m-8)x+m-5
a: Trường hợp 1: m=0
Bất phương trình sẽ là \(0x^2+3\cdot0\cdot x+0+1>0\)
=>1>0(luôn đúng)
Trường hợp 2: m<>0
\(\text{Δ}=\left(3m\right)^2-4m\left(m+1\right)\)
\(=9m^2-4m^2-4m=5m^2-4m\)
Để phương trình có nghiệm đúng với mọi số thực x thì \(\left\{{}\begin{matrix}m\left(5m-4\right)< 0\\m>0\end{matrix}\right.\Leftrightarrow0< m< \dfrac{4}{5}\)
Vậy: 0<=m<4/5
b: Trường hợp 1: m=4
\(g\left(x\right)=\left(4-4\right)\cdot x^2+\left(2\cdot4-8\right)x+4-5=-1< 0\)(luôn đúng)
Trường hợp 2: m<>4
\(\text{Δ}=\left(2m-8\right)^2-4\left(m-4\right)\left(m-5\right)\)
\(=4m^2-32m+64-4\left(m^2-9m+20\right)\)
\(=4m^2-32m+64-4m^2+36m-80\)
=4m-16
Để bất phương trình luôn âm thì \(\left\{{}\begin{matrix}4m-16< 0\\m-4< 0\end{matrix}\right.\Leftrightarrow m< 4\)
Vậy: m<=4
Đúng 0
Bình luận (0)
Câu 1 a.tìm tất cả các giá trị của tham số m để bất phương trình mx²+3mx+(m+1)>0 nghiệm đúng với mọi số thực x?
b.tìm các giá trị của m để biểu thức sau luôn âm:g(x)=(m-4)x²+(2m-8)x+m-5
Xác định các giá trị của m để phương trình x^2 -x+1-m =0 có hai nghiệm x1;x2 thỏa mãn đẳng thức \(5.\left(\dfrac{1}{x1}+\dfrac{1}{x2}\right)-x1.x2+4=0\)
Mọi người ơi, giúp em bài này với ạ, em cần rất gấp ạ, em cảm ơn rất nhiều ạ. (Nếu có thể giải chí tiết phần thay S và P vào đẳng thức được không ạ? Em cảm ơn rất nhiều ạ.)
\(x^2-x+1-m=0\left(1\right)\\ \text{PT có 2 nghiệm }x_1,x_2\\ \Leftrightarrow\Delta=1-4\left(1-m\right)\ge0\\ \Leftrightarrow4m-3\ge0\Leftrightarrow m\ge\dfrac{3}{4}\\ \text{Vi-ét: }\left\{{}\begin{matrix}x_1+x_2=1\\x_1x_2=1-m\end{matrix}\right.\\ \text{Ta có }5\left(\dfrac{1}{x_1}+\dfrac{1}{x_2}\right)-x_1x_2+4=0\\ \Leftrightarrow5\cdot\dfrac{x_1+x_2}{x_1x_2}-x_1x_2+4=0\\ \Leftrightarrow\dfrac{5}{1-m}+m-1+4=0\\ \Leftrightarrow\dfrac{5}{1-m}+m+3=0\\ \Leftrightarrow5+\left(1-m\right)\left(m+3\right)=0\\ \Leftrightarrow m^2+2m-8=0\\ \Leftrightarrow m^2-2m+4m-8=0\\ \Leftrightarrow\left(m-2\right)\left(m+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}m=2\left(n\right)\\m=-4\left(l\right)\end{matrix}\right.\)
Vậy $m=2$
Đúng 2
Bình luận (0)
xác định a,b,c thõa mãn đẳng thức sau với mọi giá trị của x
(ax+b)(x^2+cx+1)=x^3-3x+2
(ax+b)(x2+cx+1)=x3-3x+2
ax3+acx2+ax+bx2+cbx+b=x3-3x+2
ax3+(acx2+bx2)+(ax+cbx)+b=X3-3x+2
ax3+x2(ac+b)+x(a+cb)+b=x3+0x2-3x+2
Đồng nhất các hệ số hai vế của đẳng thức,ta có:(dùng dấu ngoặc nhọn nha bạn)
a=1 a=1
ac+b=0 =>(dấu ngoặc nhọn) c=-2
a+cb=-3 b=2
b=2 (cái tính kết quả bạn có thế tính rõ hơn,mình làm hơi tắt)
Vậy a=1,b=2,c=-2 thì thỏa mãn đẳng thức đã cho
(Nếu không hiểu các bạn có thể xem trên google chuyên dề phương pháp hệ số bất định của bài phân tích đa thức thành nhân tử)
Đúng 0
Bình luận (0)
Mong các bạn ửng hộ bài giải của mình nha!
Đúng 0
Bình luận (0)
( ax + b )( x2 + cx + 1 ) = x3 - 3x + 2
<=> ax( x2 + cx + 1 ) + b( x2 + cx + 1 ) = x3 - 3x + 2
<=> ax3 + acx2 + ax + bx2 + bcx + b = x3 - 3x + 2
<=> ax3 + ( ac + b )x2 + ( a + bc )x + b = x3 - 3x + 2
<=> \(\hept{\begin{cases}a=1\\ac+b=0\\a+bc=-3\end{cases}}\)và b = 2
<=> \(\hept{\begin{cases}a=1\\b=2\\c=-2\end{cases}}\)
1,cho biểu thức \(A=\left(\frac{2x-1}{x^2-4}+\frac{x+2}{x^2-x-2}\right):\frac{x-2}{x^2+3x+2}\)
a,CMR: biểu thức A luôn dương với mọi giá trị của x thỏa mãn điều kiện xác định
b,tìm tất cả các giá trị của x để A=11
\(A=\left(\frac{2X-1}{x^2-4}+\frac{x+2}{x^2-x-2}\right):\frac{x-2}{x^2+3x+2}ĐK:x\ne\left\{2,-2,-1\right\}\)
a) \(A=\left[\frac{\left(2x-1\right)}{\left(x-2\right)\left(x+2\right)}+\frac{x+2}{\left(x+1\right)\left(x-2\right)}\right]:\frac{x-2}{\left(x+2\right)\left(x+1\right)}\)
\(A=\left[\frac{\left(2x-1\right)\left(x+1\right)}{\left(x-2\right)\left(x+2\right)\left(x+1\right)}\frac{\left(x+2\right)\left(x+2\right)}{\left(x+1\right)\left(x-2\right)\left(x+2\right)}\right].\frac{\left(x+2\right)\left(x+1\right)}{x-2}\)
\(A=\frac{2x^2+x-1+x^2+4x.4}{\left(x-2\right)\left(x+2\right)\left(x+1\right)}.\frac{\left(x+2\right)\left(x+1\right)}{\left(x-2\right)}\)
\(A=\frac{3x^2+5x+3}{\left(x-2\right)\left(x+2\right)\left(x+1\right)}.\frac{\left(x+2\right)\left(x+1\right)}{\left(x-2\right)}\)
\(A=\frac{3x^2+5x+3}{\left(x-2\right)^2}\)
Ta có :\(3x^2+5x+3\)
\(=3\left(x^2+\frac{5}{3}x+1\right)\)
\(=3\left[x^2+2.\frac{5}{6}x+\frac{25}{36}+\frac{9}{36}\right]\)
\(=3\left[\left(x+\frac{5}{6}\right)^2+\frac{9}{36}\right]>0\)
Mà \(\left(x-2\right)^2>0\)
\(\Rightarrow A>0\left(dpcm\right)\)
\(b,A=11\Leftrightarrow\frac{3x^2+5x+3}{\left(x-2\right)^2}=11\)
\(\Rightarrow3x^2+5x+3=11.\left(x-2\right)^2\)
\(\Rightarrow3x^2+5x+3=11.\left(x^2-4x+4\right)\)
\(\Rightarrow8x^2-49x+41=0\)
\(\Rightarrow8x^2-8x-41x+41=0\)
\(\Rightarrow8x\left(x-1\right)-41\left(x-1\right)=0\)
\(\Rightarrow\left(8x-41\right)\left(x-1\right)=0\)
\(\Leftrightarrow\hept{\begin{cases}8x-41=0\\x-1=0\end{cases}\Rightarrow\hept{\begin{cases}x=\frac{41}{8}\\x=1\end{cases}}}\)(Thỏa mãn)
Tìm tất cả các giá trị của m để bất phương trình
2
|
x
-
m
|
+
x
2
+
2
2
m
x
thỏa mãn với mọi x A.
m
-
2
B. không tồn tại m C.
-
2
m
2
D.
m
2
Đọc tiếp
Tìm tất cả các giá trị của m để bất phương trình 2 | x - m | + x 2 + 2 > 2 m x thỏa mãn với mọi x
A. m > - 2
B. không tồn tại m
C. - 2 < m < 2
D. m < 2