Khai triển nhị thức (2x-3)^6
TP
Những câu hỏi liên quan
Tìm hệ số của số hạng chứa x 3 trong khai triển nhị thức Niutơn ( 2 x - 1 ) 6
A. 160
B. -960
C. 960
D. -160
Chọn D
Xét khai triển nhị thức Niutơn:
(
2
x
-
1
)
6
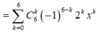
Số hạng chứa x 3 trong khai triển ứng với k = 3.
Vậy hệ số của số hạng chứa
x
3
trong khai triển là: ![]() .
.
Đúng 0
Bình luận (0)
Có bao nhiêu số hạng trong khai triển nhị thức ( 2 x - 3 ) 2018 thành đa thức.
A. 2018
B. 2019
C. 2020
D. 2017
Chọn B
![]()
![]()
![]()
Vậy khai triển trên có 2019 số hạng.
Đúng 0
Bình luận (0)
Sổ các hạng tử trong khai triển của nhị thức nếu tơn (2x + 3) ^ 7 là
SỐ các hạng tử là 8 hạng tử
Đúng 0
Bình luận (0)
Viết khai triển (2x-3y)^10 bằng nhị thức Newton
\(\left(2x-3y\right)^{10}\)
\(=\left(2x\right)^{10}-C^1_{10}\cdot\left(2x\right)^9\cdot3y+C^2_{10}\cdot\left(2x\right)^8\cdot\left(3y\right)^2+...+\left(3y\right)^{10}\)
\(=1024x^{10}-1536x^9y+...+59049y^{10}\)
Đúng 0
Bình luận (0)
Có bao nhiêu số hạng trong khai triển nhị thức
2
x
-
3
2018
thành đa thức A. 2019. B. 2020. C. 2018. D. 2017.
Đọc tiếp
Có bao nhiêu số hạng trong khai triển nhị thức 2 x - 3 2018 thành đa thức
A. 2019.
B. 2020.
C. 2018.
D. 2017.
Ta có:
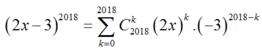
do đó khai triển trên có 2019 số hạng.
Chọn A.
Đúng 0
Bình luận (0)
Tìm hệ số của x 3 trong khai triển nhị thức
2 x + 1 x 13
A. 366080
B. 286
C. 3660
D. 36608
Số hạng tổng quát trong khai triển là C k 13 . 2 13 - k . x 13 - 5 / 2 k
Ta cần có 13-5/2 k= 3 ↔k=4. Do đó hệ số của x3 là C134.29= 366080
Chọn D
Đúng 0
Bình luận (0)
Có bao nhiêu số hạng trong khai triển nhị thức
2
x
-
3
2018
A. 2018. B. 2020. C. 2019. D. 2017.
Đọc tiếp
Có bao nhiêu số hạng trong khai triển nhị thức 2 x - 3 2018
A. 2018.
B. 2020.
C. 2019.
D. 2017.
Trong khai triển nhị thức a + b n thì số các số hạng là n+1 nên trong khai triển 2 x - 3 2018 có 2019 số hạng.
Đáp án C
Đúng 0
Bình luận (0)
Có bao nhiêu số hạng trong khai triển nhị thức
2
x
-
3
2018
A. 2018. B. 2020. C. 2019. D. 2017.
Đọc tiếp
Có bao nhiêu số hạng trong khai triển nhị thức 2 x - 3 2018
A. 2018.
B. 2020.
C. 2019.
D. 2017.
Đáp án C
Trong khai triển nhị thức a + b n thì số các số hạng là n + 1 nên trong khai triển 2 x - 3 2018 có 2019 số hạng.
Đúng 0
Bình luận (0)
2. Trong khai triển nhị thức ( a +2)^n +6 ( n€N). Có tất cả 17 số hạng . Vậy n bằng?
6. Trong khai triển (2a -1)^6 tổng 3 số hạng đầu là?
7. Trong khai triển ( x - √y )^16 tổng hai số hạng cuối là
2/ \(\left(a+b\right)^k\Rightarrow k+1\left(so-hang\right)\)
\(\Rightarrow n+6+1=17\Rightarrow n=10\)
6/ \(\left(2a-1\right)^6=\sum\limits^6_{k=0}C^k_6.2^{6-k}.\left(-1\right)^k.a^{6-k}\)
\(\Rightarrow tong-3-so-hang-dau=C^0_6.2^6+C^1_6.2^5.\left(-1\right)+C^2_6.2^4.\left(-1\right)^2=...\)
7/ \(\left(x-\sqrt{y}\right)^{16}=\left(x-y^{\dfrac{1}{2}}\right)^{16}\)
\(\Rightarrow tong-2-so-hang-cuoi=C^{16}_{16}+C^{15}_{16}=...\)
Đúng 0
Bình luận (0)



