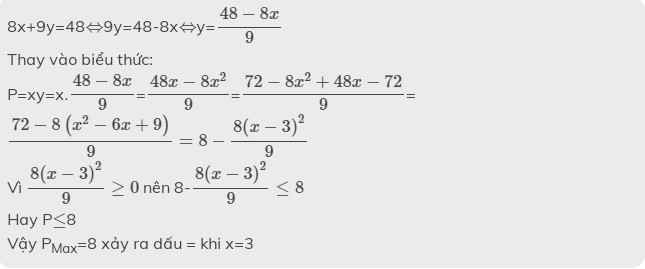Cho x,y thoả mãn 8x+3y=48, tìm GTLN của xy
CT
Những câu hỏi liên quan
Cho x, y là hai số tự nhiên khác 0, thoả mãn x+y=12. Tìm GTLN của S=xy
Áp dụng bất đẳng thức Cosi ta có:
\(x+y\ge2\sqrt{xy}\)
\(\Rightarrow2\sqrt{S}\le12\Leftrightarrow\sqrt{S}\le6\Rightarrow S\le36\)
Dấu = xảy ra khi x=y=6
Đúng 1
Bình luận (0)
Cho x,y,z thuộc R thoả mãn x+y+z=3
Tìm GTLN của A=xy+yz+xz
Cho x,y,z là các số không âm thoả mãn: x+y+z=1
Tìm GTLN của P=(x+2y+3z)(6x+3y+2z)
Áp dụng bất đẳng thức\(\left(a+b\right)^2>=4ab\)
Ta có
2P=(2x+4y+6z)(6x+3y+2z) <= (8(x+y+z)-y)^2/4 <= ((8-y)^2)/4 <= (8^2)/4= 16
Dấu "=" xảy ra khi x=1/2; y=0;z=1/2
Do đó max P=8 khi x=1/2;y=0;z=1/2
Đúng 0
Bình luận (0)
Cho các số không âm x,y,z thoả mãn 8x+3y=29 và 9x+1011z=9.Tìm giá trị lớn nhất của biểu thức A=26x+3y+2021z
Cho x,y thoả mãn 8x^2 +y^2+1/(4x^2)=4. Tìm giá trị nhỏ nhất của A=xy
Cho x, y thỏa mãn : 8x + 9y = 48. Tìm giá trị lớn nhất của tích P = xy.
Tìm các giá trị nguyên của x , y thoả mãn xy - 3y + 5 = 0
xy-3y+5=0
xy-3y=-5
y(x-3)=-5
Ta có y và x-3 thuộc Ư(5)
Bạn kẻ bảng rùi làm nốt nha
Đúng 0
Bình luận (0)
cho ác số dương x ,y ,z thả mãn x+y+z=3.Tìm GTLN của
B=\(\sqrt{\dfrac{xy}{xy+3z}}\)+\(\sqrt{\dfrac{yz}{yz+3x}}\)+\(\sqrt{\dfrac{zx}{zx+3y}}\)
Áp dụng bất đẳng thức AM - GM và kết hợp với giả thiết x + y + z = 3 ta có:
\(B=\sqrt{\dfrac{xy}{xy+z\left(x+y+z\right)}}+\sqrt{\dfrac{yz}{yz+x\left(x+y+z\right)}}+\sqrt{\dfrac{zx}{zx+y\left(x+y+z\right)}}\)
\(B=\sqrt{\dfrac{xy}{\left(x+z\right)\left(y+z\right)}}+\sqrt{\dfrac{yz}{\left(y+x\right)\left(z+x\right)}}+\sqrt{\dfrac{zx}{\left(z+y\right)\left(z+x\right)}}\le\dfrac{1}{2}\left(\dfrac{x}{x+z}+\dfrac{y}{y+z}+\dfrac{y}{y+x}+\dfrac{z}{z+x}+\dfrac{z}{z+y}+\dfrac{x}{z+x}\right)\)
\(B\le\dfrac{3}{2}\).
Đẳng thức xảy ra khi x = y = z = 1.
Vậy...
Đúng 2
Bình luận (0)
Tìm GTLN và GTNN : A = x^2 + y^2 biết x, y thoả mãn x^2 + y^2 - xy = 4 .