Nhờ quý thầy cô giảng giúp bài toán này cho bé. Mẹ cám ơn ạ
LM
Những câu hỏi liên quan
Tìm các số nguyên tố \(p;q;r;s\) phân biệt sao cho \(p^3+q^3+r^3+s^3=1709\)
P/s: Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán , gợi ý giúp đỡ em bài toán với ạ!
Em cám ơn nhiều lắm ạ!
Tìm tất cả các số nguyên tố \(p\) sao cho \(2^p+p^2\) cũng là số nguyên tố ?
P/s: Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán giúp đỡ em bài toán về chủ đề : Đồng Dư Thức với ạ!
Em cám ơn nhiều ạ!
Với p = 2 => 2p + p2 = 8 (loại)
Với p = 3 => 23 + 32 = 17 (loại)
Nhận thấy với p > 3 => p lẻ
Đặt p = 3k + 1 ; p = 3k + 2 (k \(\in Z^+\))
Khi đó P = 2p + p2
= (2p + 1) + (p2 - 1)
Vì p lẻ => 2p + 1 = (2 + 1).(2p - 1 - 2p - 2 + ... + 1) \(⋮3\)(1)
Với p = 3k + 1 => p2 - 1 = (p - 1)(p + 1) = (3k + 1 - 1)(3k + 1 + 1)
= 3k(3k + 2) \(⋮3\) (2)
Từ (1) ; (2) => P \(⋮3\)(loại)
Với p = 3k + 2 => p2 - 1 = (p - 1)(p + 1) = (3k + 2 - 1)(3k + 2 + 1)
= 3(k + 1)(3k + 1) \(⋮\)3 (3)
Từ (1) ; (3) => P \(⋮3\)
=> p = 3 là giá trị cần tìm
Đúng 1
Bình luận (1)
Tìm tất cả các số nguyên tố \(p_1;p_2;p_3;...;p_8\) sao cho
\(p_1^2+p_2^2+p_3^2+.......+p_7^2=p^2_8\)
P/s: Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán, gợi ý giúp đỡ em bài toán về chủ đề số học với ạ!
Em cám ơn nhiều lắm ạ!
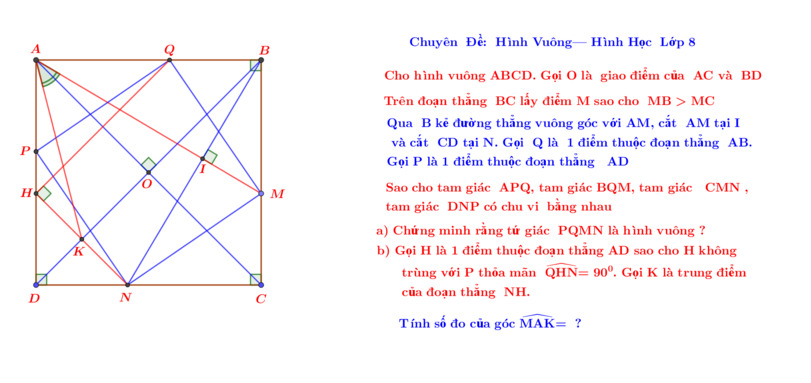
Em xin phép nhờ quý thầy cô và các bạn giúp đỡ với ạ, em cám ơn nhiều ạ
-Để mình suy nghĩ ngồi làm cho bạn nhé.
Đúng 0
Bình luận (0)
-Vì bài dài quá nên mình nói tóm tắt:
a) -Bạn chứng minh △ABM = △BCN (g-c-g) do có \(AB=BC\) , \(\widehat{BCN}=\widehat{ABM}=90^0\),\(\widehat{NBC}=\widehat{MAB}\) (bạn tự chứng minh).
-Suy ra: \(BM=CN\) .
-Suy ra 2 điều:
+\(QM^2-BQ^2=MN^2-MC^2\)
+\(QM+BQ=MN+MC\) (1)
\(QM^2-BQ^2=MN^2-MC^2\)
\(\Rightarrow\left(QM-BQ\right)\left(QM+BQ\right)=\left(MN-MC\right)\left(MN+MC\right)\)
\(\Rightarrow QM-BQ=MN-MC\) (2)
-Từ (1),(2) suy ra \(QM=MN\) nên △BMQ=△CNM (ch-cgv).
\(\Rightarrow\) MQ vuông góc với MN (bạn tự c/m).
\(QM=MN\) nên \(BQ=MC\) nên \(AQ=BM\Rightarrow PQ^2-AP^2=QM^2-BQ^2;QM+BQ=PQ+AP\)
Nên \(PQ=QM;\Delta APQ=\Delta BQM\) nên PQ⊥QM ; AP=BQ nên PQ=AQ
-Từ PQ=AQ bạn tự c/m PN=PQ (theo sườn mình đã cho) rồi sau đó c/m tam giác APQ=tam giác DNP rồi từ đó suy ra PQ vuông góc PN
.......
Đúng 0
Bình luận (1)
Xin phép nhờ quý thầy cô và các bạn giúp đỡ với ạ. Em cám ơn nhiều
Tìm tất cả các số nguyên tố \(p\) sao cho \(8.p^2+1\) là số nguyên tố
P/s: Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán hỗ trợ giúp đỡ em với ạ!
Em cám ơn nhiều ạ!
Với p = 2 => 8p2 +1 = 33 (loại)
Với p = 3 => 8p2 + 1 = 73 (tm)
Với p > 3 => Đặt p = 3k + 1 ; p = 3k + 2 (k \(\in Z^+\))
Với p = 3k + 1 => 8p2 + 1 = 8(3k + 1)2 + 1
= 72k2 + 48k + 9 = 3(24k2 + 16k + 3) \(⋮3\)(loại)
Với p = 3k + 2 => 8p2 + 1 = 8(3k + 2)2 + 1
= 72k2 + 96k + 33 = 3(24k2 + 32k + 11) \(⋮3\)(loại)
Vậy p = 3 thì 8p2 + 1 \(\in P\)
Đúng 1
Bình luận (1)
- Với \(p=2\) ko thỏa mãn
- Với \(p=3\Rightarrow8p^2+1=73\) là số nguyên tố (thỏa mãn)
- Với \(p>3\Rightarrow p^2\equiv1\left(mod3\right)\)
\(\Rightarrow p^2=3k+1\)
\(\Rightarrow8p^2+1=8\left(3k+1\right)+1=24k+9=3\left(8k+3\right)\) là số lớn hơn 3 và chia hết cho 3
\(\Rightarrow8p^2+1\) là hợp số (ktm)
Vậy \(p=3\) là SNT duy nhất thỏa mãn yêu cầu
Đúng 2
Bình luận (1)
Em xin phép được nhờ quý thầy cô và các bạn giúp đỡ!
Em cám ơn nhiều lắm ạ!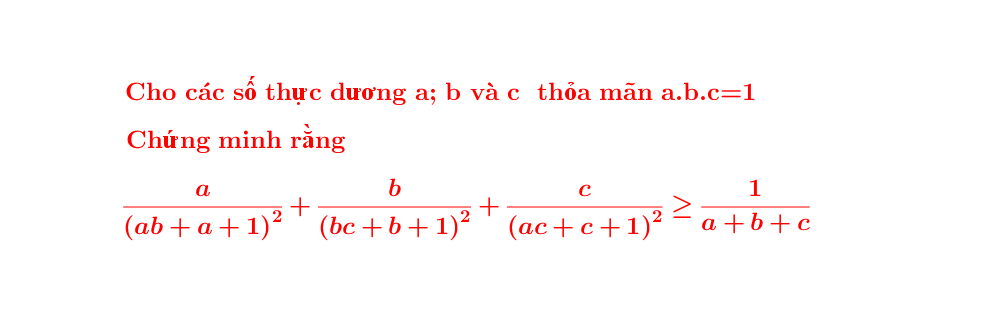
Tìm tất cả các bộ năm số nguyên tố thỏa mãn tổng lũy thừa bậc bốn của các số này bằng tích của chúng ?
P/s: Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán, gợi ý giúp đỡ em tham khảo với ạ!
Em cám ơn nhiều lắm ạ!
Em nhờ quý thầy cô giáo và các bạn giúp đỡ ý c câu hình học với ạ, em cám ơn rất nhiều ạ!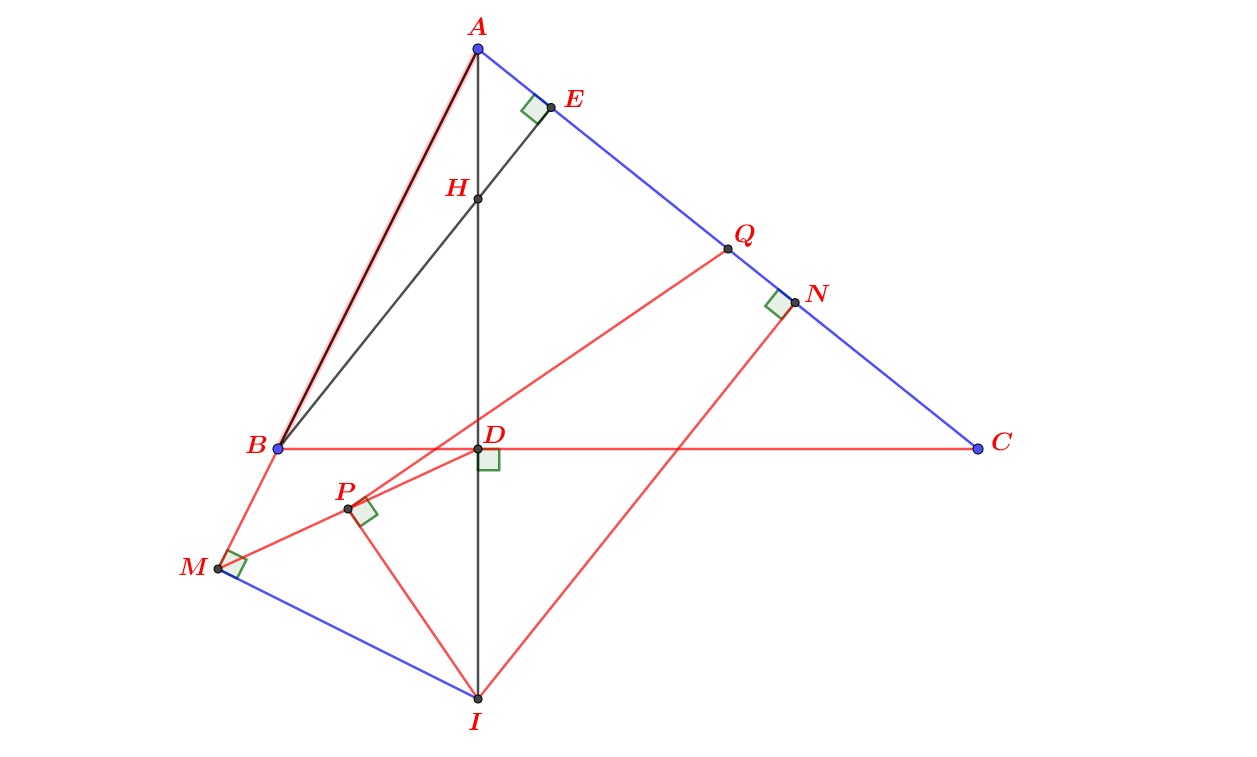

-Sao bạn đăng bài lớp 8 rồi đăng bài lớp 9 vậy?
Đúng 0
Bình luận (0)




